VGGNet

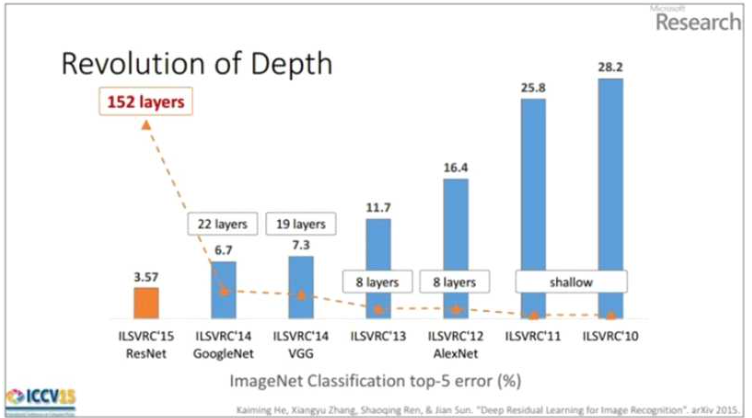
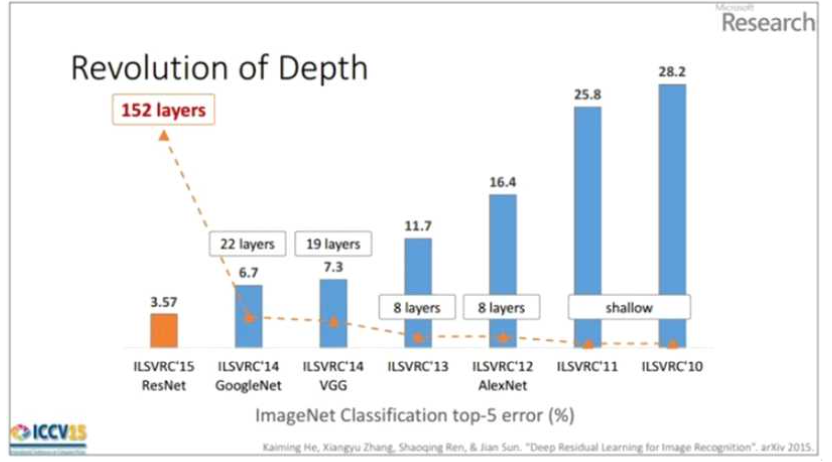
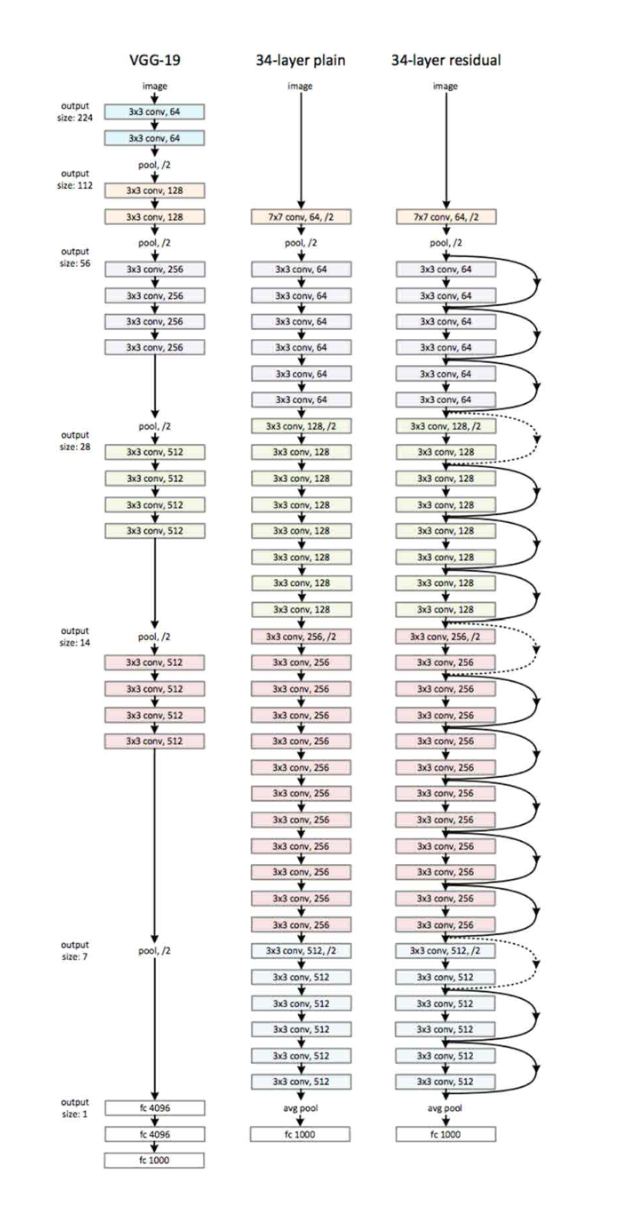
2012년, 2013년 우승 모델들은 8개의 층으로 구성된 반면 2014년의 VGGNet(VGG19)은 19 층으로, GoogleNet은 22층으로 구성되었다. 그리고 2015년에 이르러서는 152개의 층으로 구 성된 ResNet이 제안되었다. 이를 통해 네크워크가 깊어질수록 성능이 좋아졌음을 확인할 수 있다. VGGNet은 간단한 구조와 단일 네트워크에서의 좋은 성능 덕분에 GoogleNet보다 많은 네트워크에서 응용되고 있다.

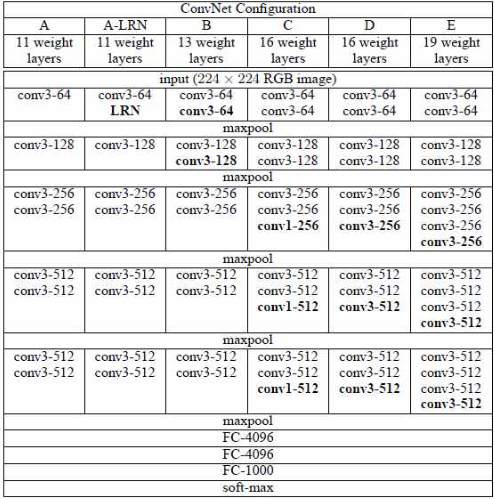
VGGNet은 네트워크의 깊이가 성능에 어떤 영향을 미치는지 연구하기 위해 설계되었다. VG G 연구팀은 깊이의 영향만을 최대한 확인하고자 컨볼루션 필터의 커널 사이즈를 가장 작은 3 x3으로 고정하고 패딩 사이즈를 1로 고정했다. 또한 컨볼루션을 통해 이미지 resize를 하는 것이 아닌 max pooling을 사용해서 이미지 resize를 하는데, 이때 max pooling의 커널 사 이즈는 2x2이고, stride는 2로 이미지를 절반으로 resize 한다.

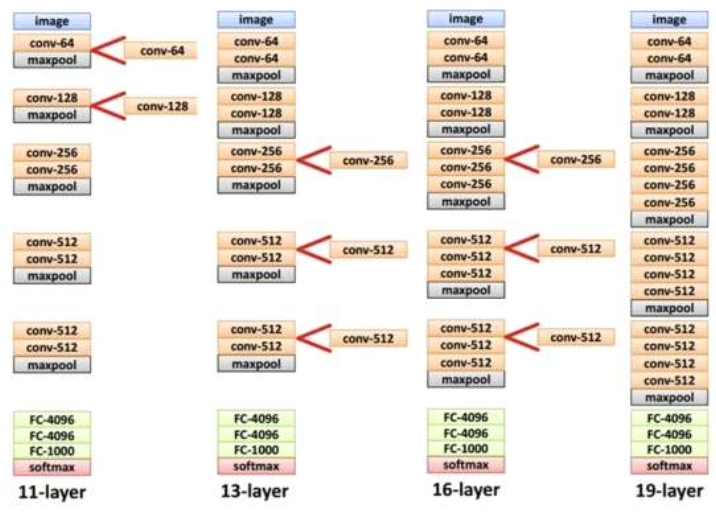
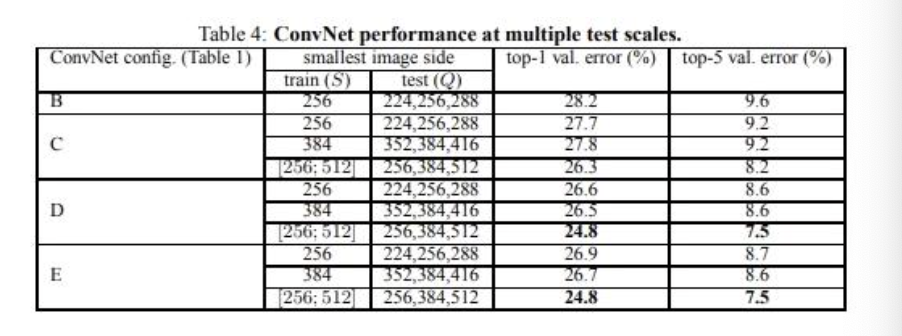
VGG 연구팀은 original 논문에서 깊이에 따른 성능 변화를 비교하기 위해 총 6개의 구조를 만들어서 성능을 비교했다. 이중 D 구조를 VGG16, E 구조를 VGG19라고 보면 되며, 네트워 크의 깊이는 컨볼루션 레이어를 추가함으로써 깊어진다.

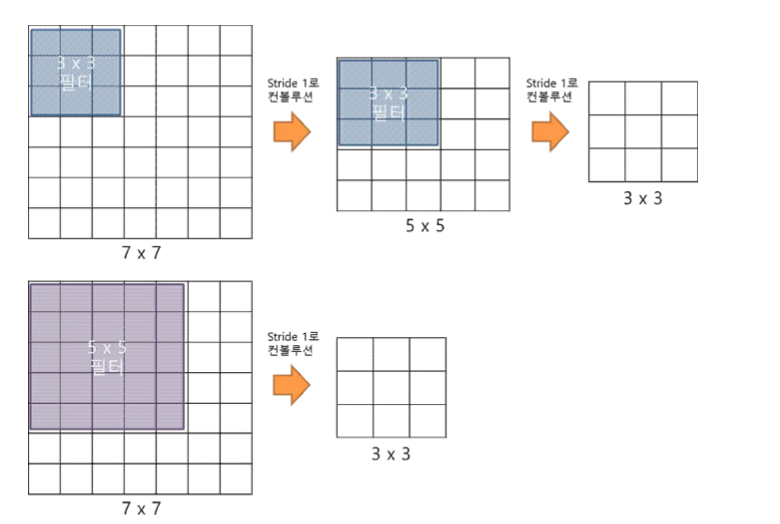
3x3 필터로 두 번 컨볼루션 하는 것과 5x5 필터로 한 번 컨볼루션 하는 것은 결과적으로 동 일한 사이즈의 특성맵을 산출한다. 즉, 3x3 필터로 두 번 컨볼루션 하는 것은 5x5 필터로 한 번 컨볼루션 하는 것과 대응된다. 그러나 성능에서는 3x3 필터로 두 번 컨볼루션 하는 것이 더 좋다.

3x3 필터가 2개일 때 5x5 필터가 1개일 때보다 적은 수의 가중치를 갖는다. CNN에서 가중 치는 모두 훈련이 필요하므로, 가중치가 적을수록 훈련을 적게 하게 되어 학습의 속도가 빨라 진다. 동시에 층의 수가 늘어나면서 비선형 함수 ReLU가 더 많이 들어가서 학습이 더 잘 된 다. 하지만 최종단에 fully-connected 3개가 붙어있어서 parameter의 수가 너무 많아진다는 단점이 있다.

깊이가 11층, 13층, 16층, 19층으로 깊어지면서 분류 에러가 감소하며, 이는 층이 깊어질수 록 성능이 좋아짐을 의미한다. 하지만 D와 E를 비교하면 에러가 비슷하거나 더 나빠지는 것 을 볼 수 있다. 이를 보완하여 설계한 네트워크가 다음에 나올 ResNet이다.

ResNet

ResNet은 마이크로소프트에서 개발한 알고리즘으로, 층수에 있어서 급속도로 깊어진다. 201 4년의 GoogleNet이 22개의 층으로 구성된 것에 비해 ResNet은 약 7배나 깊어진 152개의 층 을 갖는다. 또한 네트워크가 깊어지면서 top-5 error가 낮아지고 성능이 좋아진다.

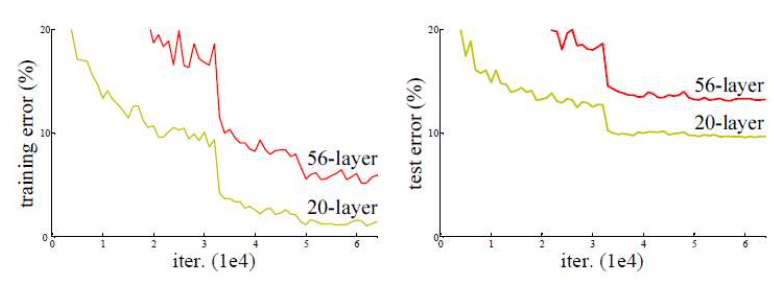
ResNet의 저자들은 망이 깊어질수록 무조건 성능이 좋아지는 것인지 확인하기 위해 20-lay er와 56-layer에 대해서 성능을 비교하는 테스트 진행했다. 그 결과 더 깊은 구조를 갖는 56 -layer가 20-layer보다 더 나쁜 성능을 보였다.

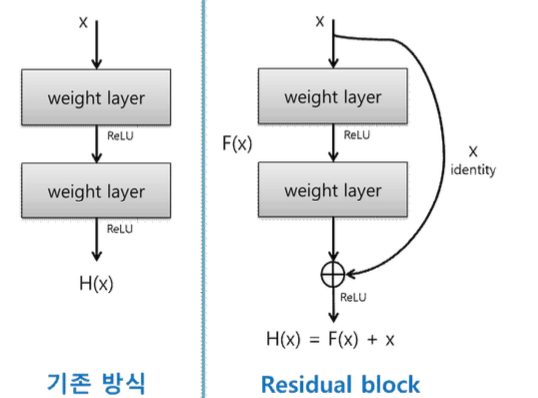
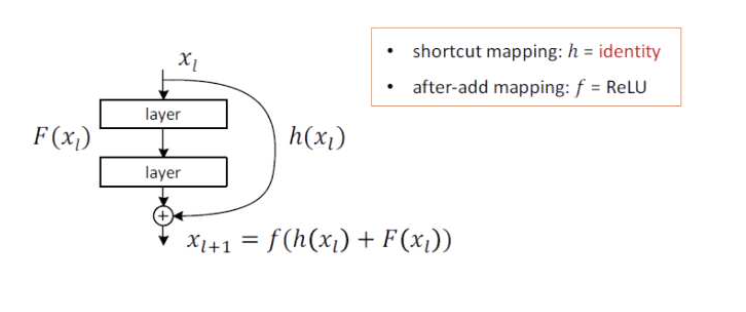
ResNet의 저자들은 새로운 방법을 이용하여 망을 깊게 만들어야 효과를 볼 수 있다는 것을 깨달았고, ResNet의 핵심인 Residual Block을 설계했다. 기존의 망과 차이가 있다면 입력값 을 출력값에 더해줄 수 있도록 지름길을 하나 만들어준 것뿐이다.

왼쪽과 같은 평범한 망은 입력 x를 받아 2개의 weighted layer를 거쳐 출력 H(x)를 내며, 다음 layer의 입력으로 적용된다. 반면, ResNet은 layer의 입력을 출력에 바로 연결시키는 ‘s kip connection’을 사용한다.

기존의 신경망은 입력값 x를 출력값 y로 매핑하는 함수 H(x)를 얻는 것이 목적이었다. 그러 나 ResNet은 F(x) + x를 최소화하는 것을 목적으로 한다. x는 현시점에서 변할 수 없는 값이 므로 F(x)를 0에 가깝게 만드는 것이 목적이 된다. F(x)가 0이 되면 출력과 입력이 모두 x로 같아지게 된다. F(x) = H(x) - x이므로 F(x)를 최소로 해준다는 것은 H(x) - x를 최소로 해주 는 것과 동일한 의미를 지닌다. 여기서 H(x) - x를 잔차(residual)라고 한다. 즉, 잔차를 최소 로 하는 것이 목적이므로 ResNet이란 이름이 붙게 되었다. x가 그대로 skip connection이 되기 때문에 연산의 증가가 없고, F(x)가 몇 개의 layer를 포함할지 선택이 가능하다. 또한 x 와 H(x)의 dimension이 다르면 dimension을 맞추기 위해 parameter를 추가해서 학습시킨 다.