비트마스크란?
비트마스크(BitMask)는 비트 연산을 이용하여 집합을 표현하거나 상태를 관리하는 방법이다.
- 이진수: 하나의 비트(bit)가 표현할 수 있는 두 가지 경우. 0 또는 1
비트마스크 장점
1. 메모리를 적게 사용
비트마스크는 집합이나 상태를 효율적으로 표현할 수 있어 메모리 사용을 최적화한다.
각 비트는 단일 상태 또는 요소의 존재 여부를 나타내므로, 대규모 데이터셋에서도 메모리 사용을 줄일 수 있다.
예를 들어, 10개의 비트는 2^10(1024)가지의 서로 다른 상태를 나타낼 수 있다.
이는 메모리 측면에서 매우 효율적이며, 많은 데이터를 미리 계산하여 저장할 수 있게 된다.
2. 연산 속도를 빠름
비트 연산은 하드웨어 수준에서 지원되며, 각 비트 연산은 매우 빠르게 처리된다.
따라서 집합 연산이나 상태 확인 등의 연산이 빠르게 수행된다.
3. 짧은 코드
비트마스크를 사용하면 간결하고 직관적인 코드를 작성할 수 있다.
비트 연산을 통해 복잡한 집합 연산이나 상태 관리를 간단하게 처리할 수 있으며, 이는 코드의 가독성과 유지보수성을 향상시킨다.
비트 연산자
비트 연산자는 이진수를 대상으로 수행되는 연산을 지원한다.
AND (&)
두 비트가 모두 1일 때만 결과가 1이 된다.
1010 & 1100→1000
OR (|)
두 비트 중 하나 이상이 1일 때 결과가 1이 된다.
1010 | 1100→1110
XOR (^)
두 비트가 서로 다를 때 결과가 1이 된다.
1010 ^ 1100→0110
NOT (~)
비트를 반전시킨다. 0은 1로, 1은 0으로
~1010→0101
왼쪽 시프트 (<<)
비트를 왼쪽으로 이동시킨다.
110011 << 1→1001101010 << 2→101000
오른쪽 시프트 (>>)
비트를 오른쪽으로 이동시킨다.
-1010 >> 1 → 0101
110011 >> 2→001100
주의할 점!
✔︎ C++나 자바에서 비트 연산자의 우선순위는 == 혹은 != 등의 비교 연산자보다 낮다.
✔︎ NOT(~) 연산에서는 입력된 비트 수보다 많은 비트 연산에 대해 주의해야 한다.
✔︎ 왼쪽 시프트(<<) 연산에서는 오버플로(overflow)에 대해 주의해야 한다.
✔︎ 오른쪽 시프트(>>) 연산에서는 부호 있는 데이터에서의 연산에 주의해야 한다.
비트마스크를 이용한 집합 구현
비트마스크를 사용하는 대표적인 사례는 집합 구현이다.
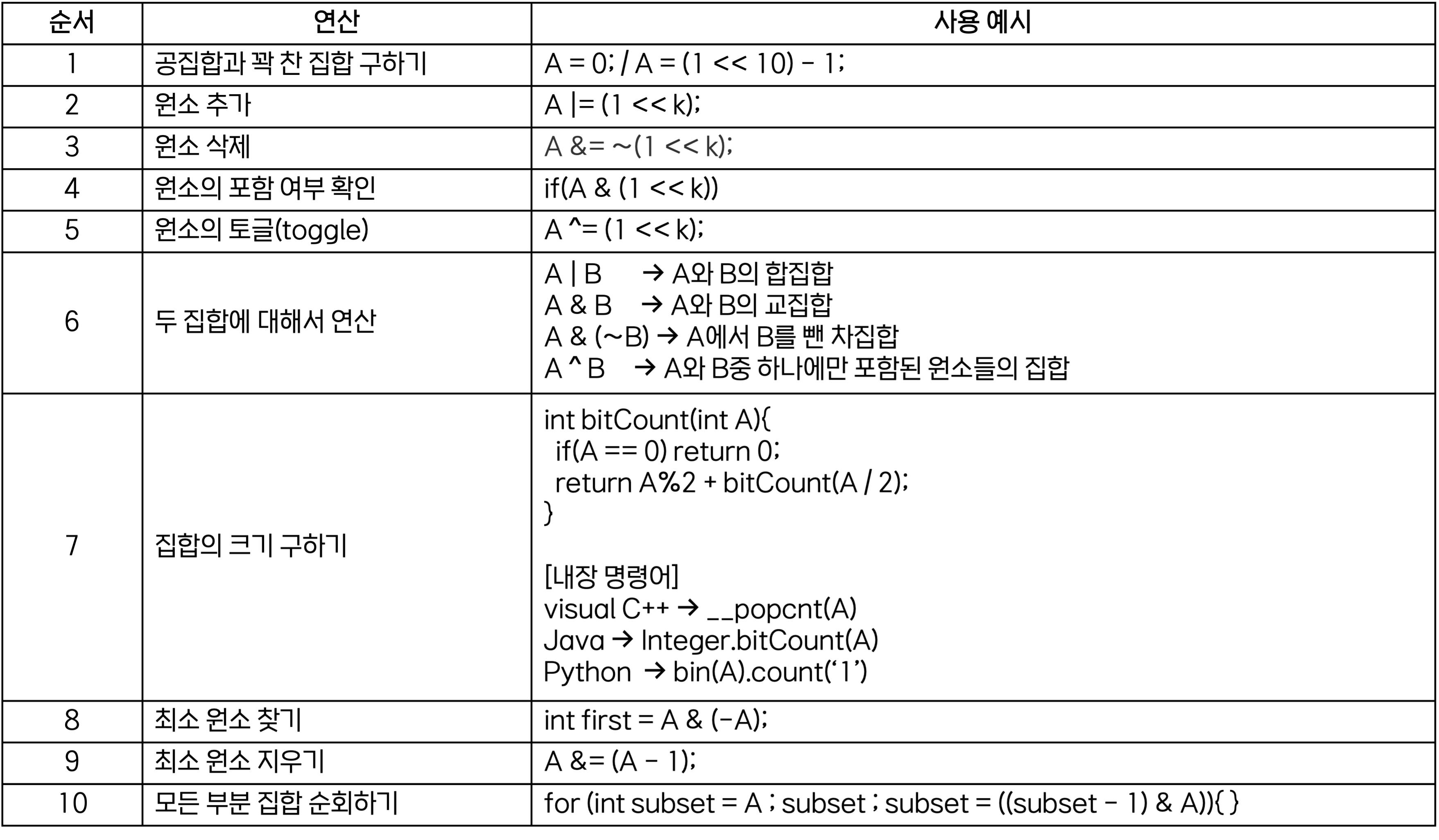
Python으로 구현해보기
class BitSet:
def __init__(self, size):
self.size = size
self.bits = 0 # 초기에는 모든 비트가 0으로 초기화된다.
def is_empty(self):
return self.bits == 0
def is_full(self):
return self.bits == (1 << self.size) - 1
def add(self, num):
self.bits |= (1 << num)
def remove(self, num):
self.bits &= ~(1 << num)
def contains(self, num):
return (self.bits & (1 << num)) != 0
def toggle(self, num):
self.bits ^= (1 << num)
def get_size(self): # size 메서드 이름을 get_size로 변경
count = 0
bits = self.bits
while bits:
count += bits & 1
bits >>= 1
return count
def min_element(self):
if self.bits == 0:
return None
return self.bits & -self.bits
def remove_min_element(self):
if self.bits == 0:
return
self.bits &= (self.bits - 1)
def iterate_subsets(self):
subset = self.bits
while subset:
print(f"Subset: {subset}")
subset = (subset - 1) & self.bits
# BitSet 클래스 사용 예제
bit_set = BitSet(20) # 0부터 19까지의 번호를 갖는 집합 생성
# 1. 공집합과 꽉 찬 집합 확인
print(f"Is bit_set empty? {bit_set.is_empty()}") # True
print(f"Is bit_set full? {bit_set.is_full()}") # False
# 2. 원소 추가
bit_set.add(4)
bit_set.add(8)
bit_set.add(12)
print(f"After adding elements: {bin(bit_set.bits)}") # 이진수로 집합 출력
# 3. 원소 삭제
bit_set.remove(8)
print(f"After removing element 8: {bin(bit_set.bits)}")
# 4. 원소의 포함 여부 확인
print(f"Contains 4: {bit_set.contains(4)}") # True
print(f"Contains 10: {bit_set.contains(10)}") # False
# 5. 원소의 토글
bit_set.toggle(4)
print(f"After toggling element 4: {bin(bit_set.bits)}")
# 6. 두 집합에 대해 연산하기 (추가 예제)
bit_set2 = BitSet(20)
bit_set2.add(4)
bit_set2.add(10)
intersection = bit_set.bits & bit_set2.bits
print(f"Intersection of bit_set and bit_set2: {bin(intersection)}")
# 7. 집합의 크기 구하기
print(f"Size of bit_set: {bit_set.get_size()}") # size 메서드를 get_size로 변경
# 8. 최소 원소 찾기
print(f"Minimum element in bit_set: {bit_set.min_element()}")
# 9. 최소 원소 지우기
bit_set.remove_min_element()
print(f"After removing minimum element: {bin(bit_set.bits)}")
# 10. 모든 부분 집합 순회하기
bit_set.iterate_subsets()Is bit_set empty? True
Is bit_set full? False
After adding elements: 0b1000100010000
After removing element 8: 0b1000000010000
Contains 4: True
Contains 10: False
After toggling element 4: 0b1000000000000
Intersection of bit_set and bit_set2: 0b0
Size of bit_set: 1
Minimum element in bit_set: 4096
After removing minimum element: 0b0Java로 구현해보기
public class BitSet {
private int size;
private int bits; // 비트마스크로 집합 저장
public BitSet(int size) {
this.size = size;
this.bits = 0; // 초기에는 공집합
}
public boolean isEmpty() {
return bits == 0;
}
public boolean isFull() {
return bits == (1 << size) - 1;
}
public void add(int element) {
bits |= (1 << element); // 해당 원소의 비트 켜기
}
public void remove(int element) {
if (contains(element)) {
bits &= ~(1 << element); // 해당 원소의 비트 끄기
}
}
public boolean contains(int element) {
return (bits & (1 << element)) != 0; // 해당 원소가 집합에 포함되어 있는지 여부 반환
}
public void toggle(int element) {
bits ^= (1 << element); // 해당 원소의 상태 뒤집기
}
public BitSet union(BitSet otherSet) {
BitSet newSet = new BitSet(size);
newSet.bits = bits | otherSet.bits; // 합집합 계산
return newSet;
}
public BitSet intersection(BitSet otherSet) {
BitSet newSet = new BitSet(size);
newSet.bits = bits & otherSet.bits; // 교집합 계산
return newSet;
}
public BitSet difference(BitSet otherSet) {
BitSet newSet = new BitSet(size);
newSet.bits = bits & ~otherSet.bits; // 차집합 계산
return newSet;
}
public int size() {
int count = 0;
int temp = bits;
while (temp != 0) {
count += temp & 1; // 각 비트가 켜져 있는지 확인하여 원소의 개수 세기
}
return count;
}
public int findMinimum() {
if (isEmpty()) {
return -1;
}
return bits & -bits; // 최소 원소(최하위 켜진 비트) 찾기
}
public void removeMinimum() {
if (!isEmpty()) {
bits &= (bits - 1); // 최소 원소 제거
}
}
public void iterateSubsets() {
int subset = bits;
while (subset != 0) {
System.out.println(Integer.toBinaryString(subset)); // 각 부분 집합 출력
subset = (subset - 1) & bits;
}
}
}public class BitSetMain {
public static void main(String[] args) {
BitSet bitSet = new BitSet(20);
// 원소 추가
bitSet.add(1);
bitSet.add(4);
bitSet.add(5);
bitSet.add(6);
bitSet.add(7);
bitSet.add(9);
// 원소 포함 여부 확인
System.out.println("Contains 4: " + bitSet.contains(4));
System.out.println("Contains 10: " + bitSet.contains(10));
// 원소 삭제
bitSet.remove(5);
// 원소 토글
bitSet.toggle(2);
bitSet.toggle(6);
// 두 집합에 대해 연산하기
BitSet anotherSet = new BitSet(20);
anotherSet.add(3);
anotherSet.add(6);
BitSet unionSet = bitSet.union(anotherSet);
BitSet intersectionSet = bitSet.intersection(anotherSet);
BitSet differenceSet = bitSet.difference(anotherSet);
System.out.println("Union of bitSet and anotherSet: " + unionSet);
System.out.println("Intersection of bitSet and anotherSet: " + intersectionSet);
System.out.println("Difference of bitSet and anotherSet: " + differenceSet);
// 집합의 크기 구하기
System.out.println("Size of bitSet: " + bitSet.size());
// 최소 원소 찾기
System.out.println("Minimum element in bitSet: " + bitSet.findMinimum());
// 최소 원소 삭제
bitSet.removeMinimum();
// 모든 부분 집합 순회하기
System.out.println("Iterating subsets of bitSet:");
bitSet.iterateSubsets();
}
}
Contains 4: true
Contains 10: false
Union of bitSet and anotherSet: BitSet@764c12b6
Intersection of bitSet and anotherSet: BitSet@4e0e2f2a
Difference of bitSet and anotherSet: BitSet@73d16e93
Size of bitSet: 5
Minimum element in bitSet: 2
Iterating subsets of bitSet:
1010010100
...
100
