2021.12.28

Geth

Go 기반으로 개발, 이더리움의 공식 클라이언트이다.
모든 이더리움은 자체게스 구현을 가지고 있다.

-이더리움
-이더리움 클래식
-엘라이즘
-익스팬스
-뮤지코인
-유비크

게스를 실행하려면 블록체인에 적합한 버전을 찾아서 다운로드해야 한다.

Geth compile 명령어

make geth

이더리움 기반 블록체인의 동기화

클라이언트가 처음부터, 즉 제네시스 블록부터 모든 블록과 트랜잭션을 다운로드하고 유효성 검사를 하는 경우도 있지만, 이는 매우 오래 걸리고 많은 자원을 필요로 한다.
DoS 여부 검사까지 확인하면 더 많은 기간을 소요하게 된다. 따라서 대부분의 이더리움 클라이언트는 트랜잭션의 전체 유효성 검사를 건너뛰고 블록체인의 일부에 동기화될 때까지 '빠른' 동기화를 수행하는 옵션을 포함한다.

JSON-RPC 인터페이스

JSON으로 RPC(remote procedure call) 명령을 제공.

RPC 인터페이스는 포트 8485에서 제공.
JSON-RPC API에 접근하려면 사용 가능한 각 RPC 명령에 해당하는 'Stub' 함수 호출을 제공하는 라이브러리를 이용하거나, 수동으로 request를 생성할 수 있다.

curl -X POST -H "Content-Type: application/json" --data '{"jsonrpc":"2.0", \
"method":"web3_clientVersion","params":[], "id":1}' http://localhost:8545

jsonrpc: JSON-RPC 프로토콜 버전
method: 호출할 method 명
params: method를 호출하는 동안 사용한 파라미터 값을 보유하는 구조화된 값. params는 생략 가능.

id: 클라이언트가 설정한 식별자

원격 이더리움 클라이언트

제공하는 기능 목록

• 개인키와 이더리움 주소를 지갑에서 관리
• 트랜잭션 생성, 서명 및 브로드캐스트
• 데이터 payload를 사용하여 스마트 컨트랙트와 상호 연동
• 브라우저와 DApp 간의 상호연동
• 블록 탐색기 같은 외부 서비스 링크
• 이더 단위를 변환하고 외부 소스에서 환율을 검색
• 자바스크립트 객체로서 web3 인스턴스를 웹 브라우저에 삽입
• 다른 클라이언트가 브라우저에 제공 또는 삽입한 web3 인스턴스를 사용
• 로컬 또는 원결 이더리움 노드에서 RPC 서비스로 접근

모바일 지갑

• Jaxx
• status
• Trust wallet
• Cipher Browser

브라우저 지갑

• 메타마스크
• 잭스
• 마이이더웰렛: 브라우저를 통한 공격에 노출되어 있음.
• 마이크립토
• 미스트

4강: 암호학

이더리움 계정 유형

• EOA
• Contract

EOA는 디지털 개인키, 이더리움 주소, 디지털 서명을 통해 외부 소유 계정의 이더 소유권을 확립한다.

개인키는 비공개로 유지된다.
계정 주소와 디지털 서명만 이더리움 시스템에 전송된다.

이더리움에서 사용하는 공개키 암호화 기반 시스템에서 키는 개인키와 공개키로 구성된 쌍으로 이루어진다.
공개키는 은행 계좌 번호, 개인키는 PIN과 유사하다고 생각하자.

공개키 암호화

비밀 정보가 없으면 거꾸로 계산하기 어려운 Trap Door Function를 통해서 키를 생성하고 이를 통해 정보를 보호하는 방식.

예)
매우 큰 2개의 소수의 곱을 구하는 것은 간단하지만, 특정 수가 두 개의 큰 소인수의 곱이라고 할 때 그 두 소수를 찾는 문제는 매우 어려운 문제이다.

암호학에서 유용한 수학함수의 더 발전된 범주는 타원 곡선의 산술 연산을 바탕으로 한다.
타원 곡선 산술에서 소수로 나눈 나머지를 곱하는 것은 간단하지만, 나눗셈은 사실상 불가능하다.

y = a^x % b
a: 0 < a < b인 정수
b: 소수

y를 구하는 것은 간단하지만, y를 통해 x를 구하는 것은 사실 상 불가능하다는 의미이다.

-->이산 로그 문제(Discrete logarithm problem) 라고 한다.

현재 가장 광범위하게 사용되는 것은 타원 곡선 암호화이다.

이더리움에서는 공개키 암호화를 사용하여 공개키-개인키 쌍을 만든다.
개인키는 계정에서 자금을 지출하기 위해 트랜잭션에 서명해야 하는 디지털 서명을 만드는 데 필요한 고유 정보의 접근을 제어한다.

개인키

무작위로 선택한 숫자.
이더리움 개인키를 생성하는 것은 기본적으로 1에서 2^256 사이의 숫자를 선택하는 것.
무작위로 추출한 256비트 숫자를 Keccak-256, SHA-256같은 256비트 해시 알고리즘에 공급함으로써 이루어진다.

공개키

타원 곡선 방정식을 만족하는 x,y 좌표의 집합.
결합된 2개의 숫자.
개인키가 있으면 공개키를 아는 것은 쉽지만, 공개키에서 개인키를 계산할 수는 없다.

K = k * G
K: 공개키
k: 개인키
G: 생성자 점

나눗셈이라는 계산이 존재하지 않으므로 K를 G로 나누어서 개인키를 계산할 수 없다.

타원 곡선 암호화

미국 표준기술연구소(NIST)에서 제정한 secp256k1이라는 특정 타원 곡선과 수학 상수 집합을 사용

y^2 = (x^3 + 7) over Fp
또는
y^2 % p = (x^3 + 7) % p

% p 또는 mod p: FP라고 쓰인 소수 차수 p의 유한체 상에 있음을 나타내는 것.
이 때 p = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 이다.

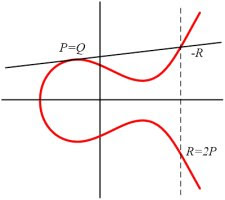
타원 곡선에서 두 점 P와 Q가 주어지면 세번째 점 R = P + Q가 타원 곡선 위에 있도록 타원 곡선 덧셈을 정의하자. 위 그림과 같이 P와 Q가 같은 점이라면 P와 Q 사이의 선은 P에서 타원의 접선일 것이다.
이 때 접선이 곡선과 교차하는 곳의 점을 -R = (x,y)이라고 하고 이를 x축 대칭한 점을 R = (x, -y)라고 하자.

무한대 점: 타원 곡선 상에서 숫자 0의 역할을 하는 점
예) P가 무한대점이면 P+Q=Q일 것.