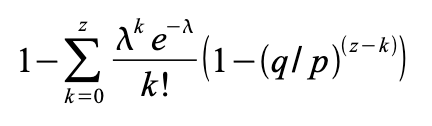Satoshi Nakamoto, Bitcoin: A Peer-to-Peer Electronic Cash System
Introduction
기존 인터넷에서의 신용 기반 전자 결제(payment)의 문제점
- 금융 기관이 필요
- 거래 비용 증가에 따른 최소 한도의 거래 규모 등으로 인해 비가역적 payment가 불가능함
전자 결제를 신용 기반이 아닌 암호학적 증명(cryptographic proof)에 기반한 제3자 없는 거래가 필요하다.
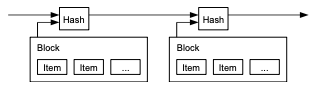
Peer-to-peer 분산 timestamp 서버를 이용한 이중 지불 문제에 대한 솔루션.
Transactions
이전 트랜잭션의 hash와 다음 owner의 public 키에 전자서명을 하고 이것을 coin(chain of digital signature)에 더한다.

문제점
- 받는 사람은 이중 지불이 일어나지는 않았는지 증명할 수 없다.
해결책
- 매 트랜잭션을 감시하는 중앙 기관을 둔다.
- coin을 제조하는 기관(mint)를 거치기에 해당 기관에 종속되는 문제점이 있다. - 모든 거래를 public하게 공개하는 방식을 사용한다.
- 참여자(node)들이 모두 동의해야 기록되는 시스템 구축 필요.
Timestamp Server
timestamp 서버에는 hash화된 block을 기록하고 공개적으로 publish한다.
각각의 timestamp는 해당 데이터가 존재한다는 것을 증명한다.
각각의 timestamp에는 이전 timestamp를 hash에 포함하고 있다.
Proof-of-Work
분산화된 timestamp 서버를 위해서는 Adam Back의 Hashcash와 유사한 작업 증명 시스템이 필요하다.
작업 증명의 특징
- 다수결 의사 결정(majority decision making)에 한 IP 당 한 표(One IP-One vote) 방식을 도입하면 여러 IP를 갖고 있는 사람에 의해 무력화될 수 있다는 문제가 있다.
- 작업 증명 방식은 One CPU - One vote 방식이다.
다수의 정직한 노드에 CPU 성능이 컨트롤된다면, 정직한 chain이 가장 긴 Chain이 될 것이다. - 과거의 block을 조작하려면 모든 블록에 대해서 작업 증명을 해야 한다.
- 작업 증명 난이도는 시간 당 블록 수의 이동 평균에 의해 결정된다.
Network
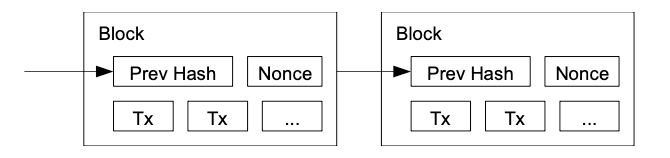
1) 모든 트랜잭션은 모든 노드에 퍼뜨려진다.
2) 개별 노드는 모든 트랜잭션을 블록에 수집한다.
3) 개별 노드는 어려운 작업 증명을 찾으려 한다.
4) 한 노드가 작업 증명을 찾으면, 모든 노드에 알린다.
5) 노드들은 해당 트랜잭션이 유효하고 소모되지 않았을 경우에만 수용한다.
6) 노드들은 허용된 블록의 hash를 previous hash로 이용하여 다음 블록을 chain에 만들어낸다.
노드들은 가장 긴 chain을 연장해 나가는데
만약 동시에 복수의 블록이 생성되었을 때는 다른 branch가 더 길어질 경우에 한하여 저장해둔다.
Incentive
첫 트랜잭션은 블록 생성자에게 코인을 지급하는 특별 트랜잭션이다.
점진적인 코인의 추가는 금 채굴자들이 금 발행을 하기 위해 자원을 투입하는 것과 같은 이치이다.
트랜잭션 수수료 또한 인센티브의 하나로 작용할 수 있다.
미리 정해둔 발행 수의 코인이 전부 지급되면, 인센티브 수단은 오로지 수수료 뿐일 것이고 inflation으로부터 자유로워질 것이다.
욕심이 많은 사람에게도 다른 노드를 속이는 것보다 새로운 코인을 채굴하는 것이 더 이득일 것이라고 판단하게 될 것이다.
Reclaiming Disk Space
코인의 최신 트랜잭션이 충분한 양의 블록에 묻히면 이미 소모된 트랜잭션은 디스크 공간을 위해 폐기될 것이다.
이를 가능케 하기 위해 트랜잭션들은 Merkle Tree에 hash화 되어 있고, block의 hash에는 Root Hash만 포함된다. 오래된 블록들은 최신 트랜잭션 hash를 제외하고 삭제되는 것이 가능하다.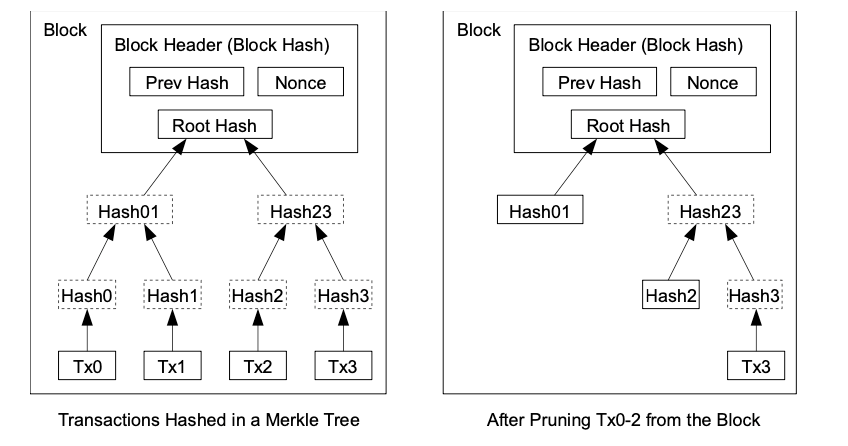
Simplified Payment Verification(SPV)
결제를 확인하기 위해서 풀노드가 돌아갈 필요 필요 없이 가장 긴 블록의 block header의 사본만 가지고 있으면 된다.
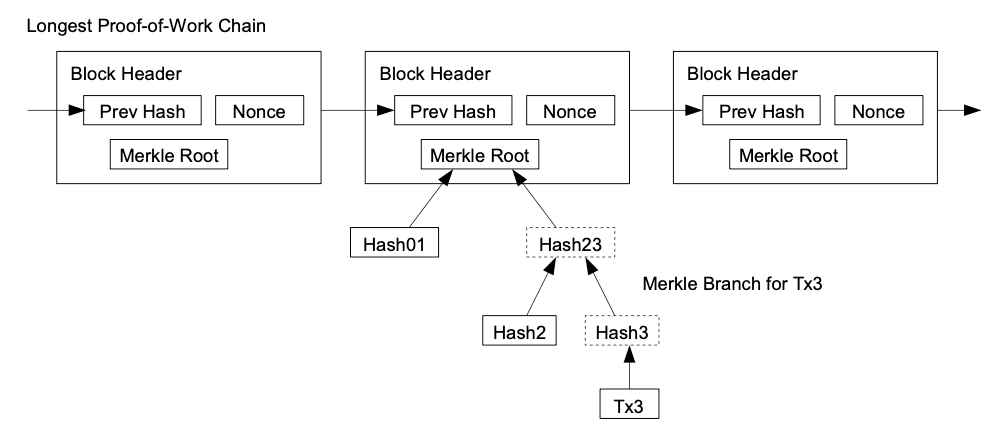
블록 정보를 요청하고 머클 트리에 있는 hash를 이용해 유효한 트랜잭션인지 확인만 하면 된다.
이러한 방식은 정직한 노드가 네트워크를 통제하면 신뢰할 수 있지만, attacker가 네트워크에 과부하를 일으키는 공격에는 취약하다.
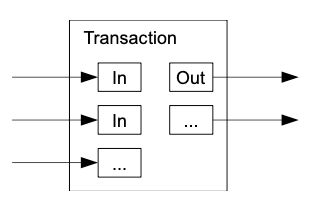
Combining and Splitting Value
개별 코인을 각각 처리하는 게 가능하나, 이를 위해 트랜잭션을 여러개 만드는 것은 바람직하지 않다. 따라서 트랜잭션에는 여러개의 input과 output이 있을 수 있도록 되어 있다.
에) 여러 input / 2개의 output(예: 지불, 거스름돈 등)
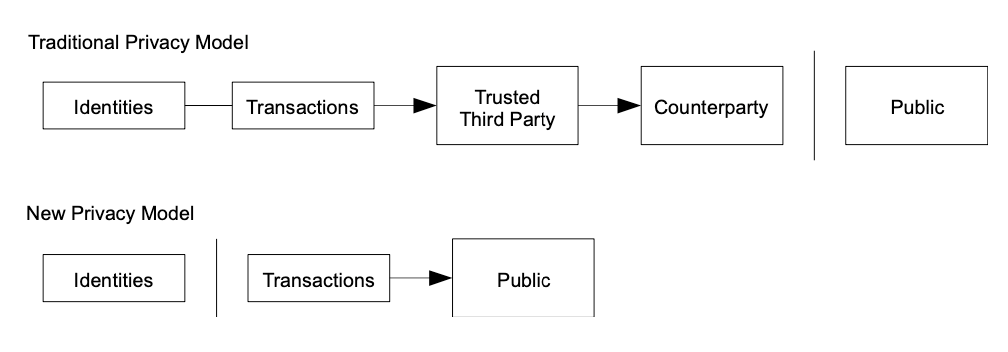
Privacy
기존의 banking model은 당사자와 신뢰할 수 있는 제3자에게만 정보가 공개됨으로써 보안이 유지된다.
모든 트랜잭션을 공개하는 경우에는 당사자에 대한 정보를 익명화함으로써 보안을 유지할 수 있다.
한 쌍의 key가 방화벽을 위해 쓰일 텐데, 이 때 키의 주인이 드러나면 당사자의 모든 트랜잭션이 공개된다는 문제점이 있다.
Calculations
공격자가 다른 chain을 생성해낸다는 것도 가능하지만 이런 경우에는 없는 값을 생성하거나 그가 소유한 적 없는 돈을 얻는 등의 행동은 불가하고, 오로지 자신이 실행한 트랜잭션을 변경하는 것만 가능하다.
정직한 노드가 chain을 늘리면 +1, 공격자가 늘리면 -1이라고 하자.
이 때 그가 정직한 체인을 따라잡을 확률은 다음과 같다.
p: 정직한 노드가 다음 블록을 찾을 확률
q: 공격자가 다음 블록을 찾을 확률
q_z: z 블록 후에 공격자가 정직한 체인을 따라잡을 확률
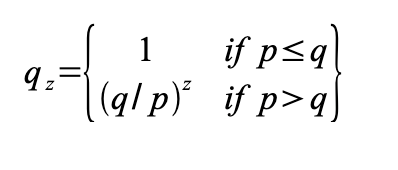
p > q이면 따라 잡아야 할 블록의 수가 늘어날 수록 확률이 지수적으로 감소하는 것을 알 수 있다.
sender(공격자)는 새로운 트랜잭션의 recipient로 하여금 sender가 돈을 지불했다고 한동안 믿게 한 다음, 다시 자신에게 돈을 보낸다. recipient가 알게 된 이후에는 이미 늦은 상태가 되는 것이다.
recipient는 세 key pair를 생성하고 서명 전에 공개키를 sender에게 준다. 이런 방식은 sender로 하여금 미리 여러 블록을 준비해 놓고 트랜잭션을 실행하는 것을 방지한다.
트랜잭션이 한 번 보내지고 나면 공격자는 다른 트랜잭션을 포함한 chain을 준비한다. recipient는 트랜잭션이 블록에 등록되고 z개의 블록이 생성될 때까지 기다린다. 그는 공격자가 얼마나 많은 연산을 수행했는지는 모르지만 정직한 정직한 노드들은 블록 당 평균 대기 시간을 가지게 된다.
공격자의 평균 기대 연산량은 다음과 같은 Poisson distribution을 가진다.
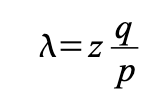
공격자가 체인을 따라 잡을 확률을 계산하려면 이제 매 진행마다 Poisson distribution을 곱해야 한다.
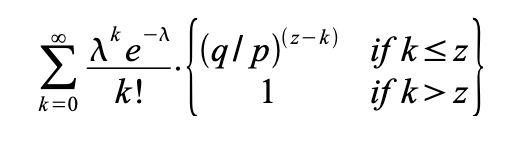
무한급수를 더하지 않게 정리하면 다음과 같다.