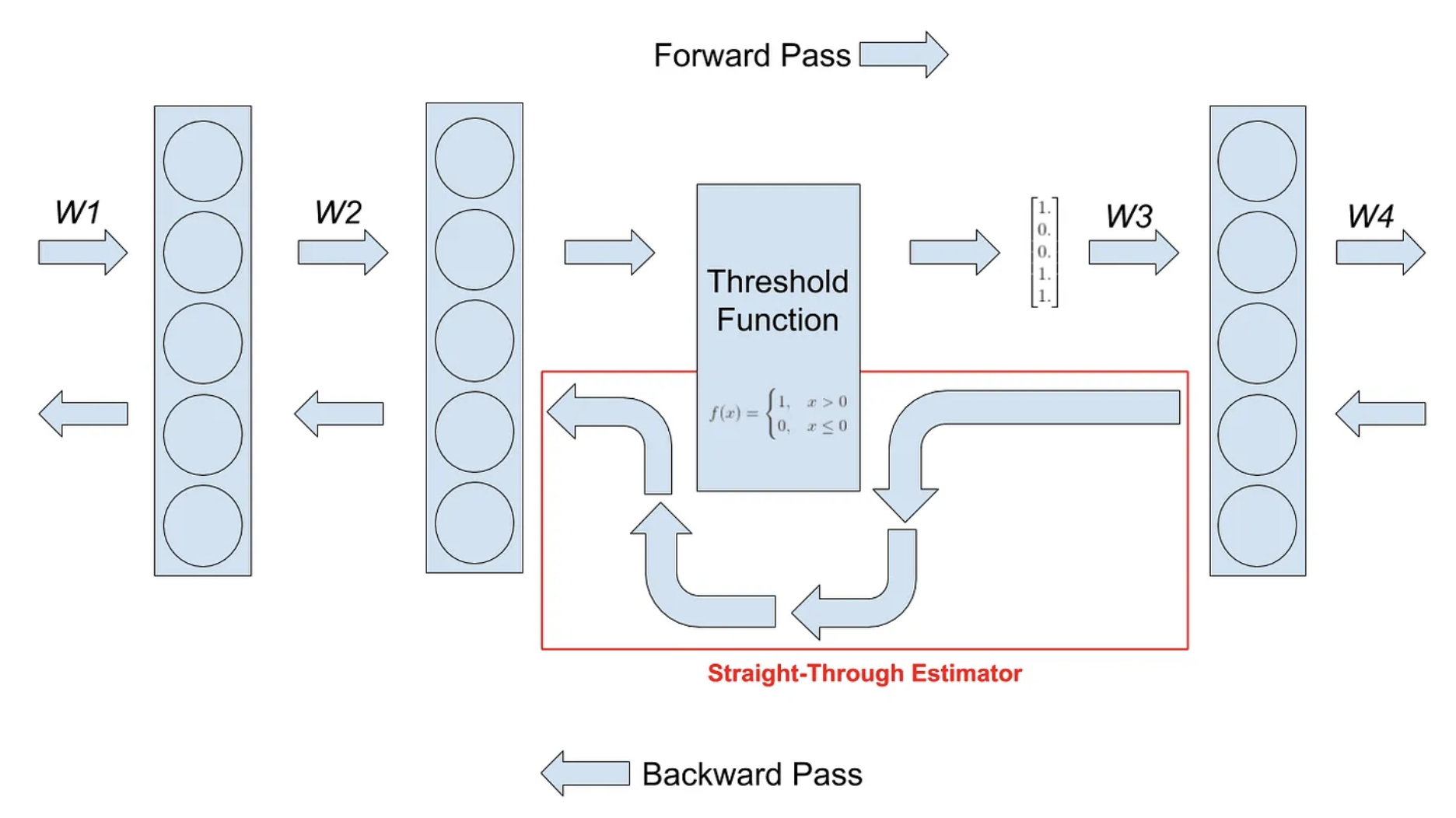
straight through estimator (STE)

• 
• 'Straight-Through Estimator' (STE)는 주로 심층 신경망 학습에 사용되는 기법
• 특히, 이산화된 값(예: 0과 1)을 사용하는 신경망 레이어에서의 그래디언트 역전파 문제를 해결하기 위해 사용됨

기본 원리:

1. 문제 정의: 일반적인 신경망 레이어는 연속적인 값(예: 실수)을 출력합니다. 하지만, 일부 레이어는 이산적인 출력(예: 0 또는 1)을 생성합니다. 이산 출력은 미분이 불가능하기 때문에, 기존의 역전파 방식을 사용하여 그래디언트를 계산하는 것이 어렵습니다.

2. STE의 역할: STE는 이산적인 레이어의 역전파 문제를 해결합니다. 순전파 단계에서는 정상적으로 이산화된 출력을 생성합니다. 하지만 역전파 단계에서는, 이산화 과정이 마치 연속적인 함수처럼 행동하는 것처럼 가정하여 그래디언트를 계산합니다.

3. 실제 구현: 예를 들어, 신경망 레이어의 출력이 특정 임계값을 기준으로 0 또는 1로 이산화됩니다. 순전파에서는 이 임계값에 따라 출력이 결정됩니다. 역전파에서는 이 이산화 과정을 무시하고, 원래의 연속적인 출력 값에 대한 그래디언트를 그대로 사용합니다.

STE의 중요성:

• 비연속적인 함수 학습: 이산적인 값을 다루는 신경망(예: 이진화된 신경망)에서 학습이 가능하게 합니다.
• 계산 효율성 증가: 이산화된 값을 사용하면 메모리 사용량과 계산 복잡도를 줄일 수 있습니다.
• 넓은 응용 가능성: 하드웨어 최적화, 자원 제한적인 환경에서의 신경망 구현 등 다양한 분야에 활용될 수 있습니다.

한계점:

• 근사적 접근: STE는 근사적인 방법이므로, 때때로 최적의 학습 경로를 찾지 못할 수 있습니다.
• 이론적 정당성 부족: STE의 이론적 기반은 아직 충분히 탐구되지 않았으며, 특정 상황에서의 효율성이나 정확성에 대한 논란이 있을 수 있습니다.

• https://hassanaskary.medium.com/intuitive-explanation-of-straight-through-estimators-with-pytorch-implementation-71d99d25d9d0