// 2020년 10월 5일 월요일 1번째 글
// 작성자: 황상훈
// 알고리즘의 수행시간을 점근적으로 표기하는 방법에 대해서 정리한다.
// 각각의 표기법들을 명확히 구분하여 헷갈리지 않도록 한다.
.
.
.
점근적 표기(asymptotic notation)란 무엇인가?
asymptotic notation.
주로 알고리즘의 수행시간을 나타내기 위해 사용하는 표기법.
점근 표기법(asymptotic notation)은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다. 알고리즘의 복잡도를 단순화할 때나 무한급수의 뒷부분을 간소화할 때 쓰인다.
(출처: 위키백과)
빅-오(O), 빅-오메가(Ω), 빅-세타(θ), 리틀-오(o), 리틀-오메가(ω)와 같은 표기법들이 있다.
이 글에서는 각각의 표기법들이 무엇을 뜻하는지 정리한다.
빅-오(O) 표기법
어떤 함수의 점근적 상한을 제시해주는 표기법.
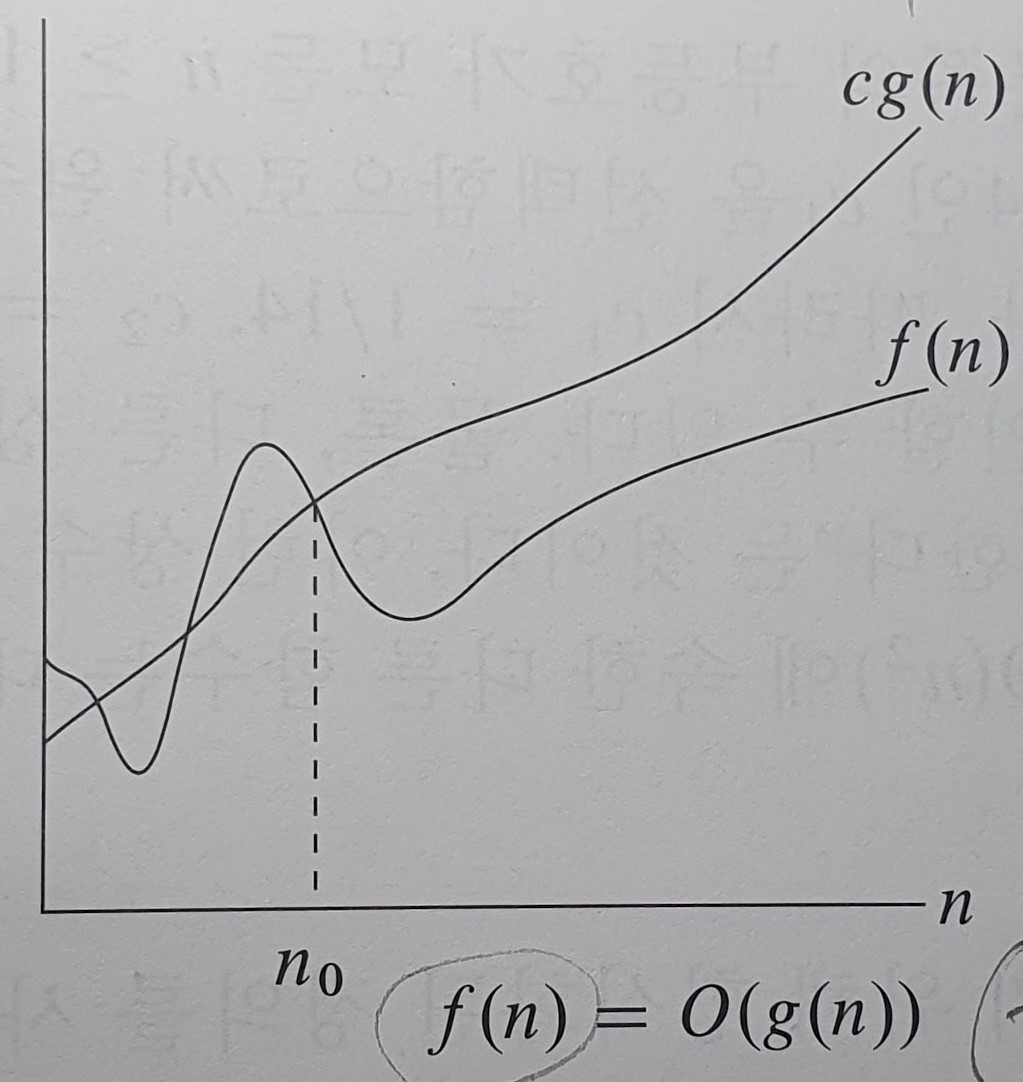
함수 f(n)이 집합 O(g(n))의 원소라는 것을 가리키기 위해 f(n) = O(g(n))이라고 쓴다.
-
f(n)이라는 함수의 수행시간은 c * g(n)이라는 함수보다 n >= n0인 지점부터 항상 작거나 같다는 뜻이고,
-
f(n) = O(g(n))이라는 표기는 f(n)이 g(n)보다 같거나 작다는 것을 보장한다는 뜻이며,
-
f(n)이라는 함수의 수행시간에서 최악의 경우라고 할 수 있다.
빅-오 표기법은 또한, 수행시간을 어느 상한점보다 낮다고 보장해주기 때문에 중요하다고 볼 수 있다.
(여담이지만, 현업에서는 효율적인 의사소통을 위해서 수행시간이라는 의미로 사용한다는 이야기가 있다, 빅-오 표기법의 특성과 중요성을 깨달을 수 있다면 이해하기 쉬울 것이다.)
빅-오메가(Ω) 표기법
어떤 함수의 점근적 하한을 제시해주는 표기법.
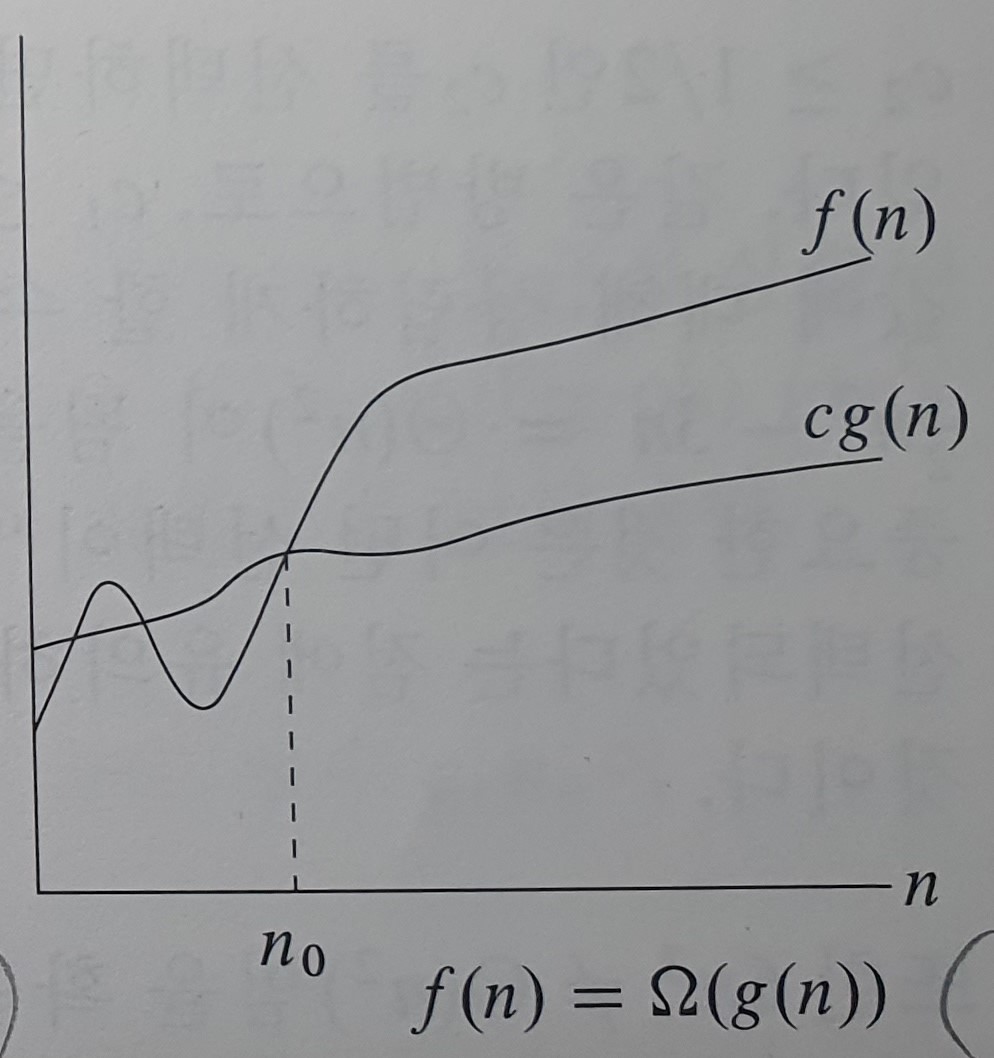
함수 f(n)이 집합 Ω(g(n))의 원소라는 것을 가리키기 위해 f(n) = Ω(g(n))이라고 쓴다.
-
f(n)이라는 함수의 수행시간은 c * g(n)이라는 함수보다 n >= n0인 지점부터 항상 크거나 같다는 뜻이고,
-
f(n) = Ω(g(n))이라는 표기는 f(n)이 g(n)보다 같거나 크다는 것을 보장한다는 뜻이며,
-
f(n)이라는 함수의 수행시간에서 최선의 경우라고 할 수 있다.
빅-오메가 표기법은 다음에서 설명할 빅-세타 표기법을 이해하기 위해서 꼭 이해하고 넘어가야 한다.
빅-세타(θ) 표기법
어떤 함수의 점근적으로 엄밀한 한계를 제시해주는 표기법.
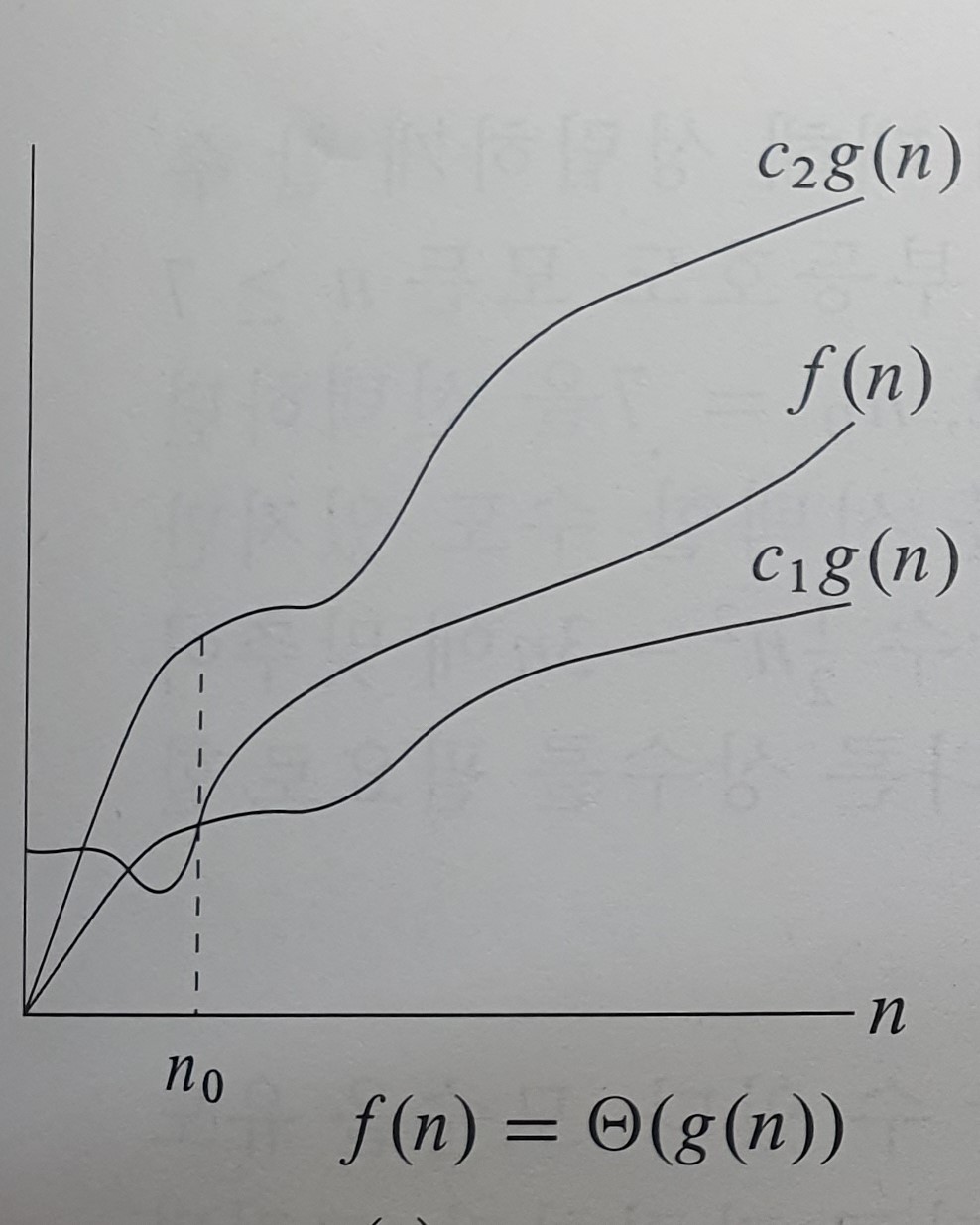
위에서 정리한 빅-오와 빅-오메가 두 개를 전부 만족하는 경우에 빅-세타를 만족한다고 할 수 있다.
여기까지 빅-오와 빅-오메가, 빅-세타 표기법에 대해서 정리했다.
그렇다면, 아직 설명하지 않은 리틀-오 표기법과 리틀-오메가 표기법은 무엇일까?
두 가지 표기법을 설명하기에 앞서서, 그러한 표기 들이 왜 필요한지 생각해보기로 한다.
//
빅-오 표기법은 어떤 함수의 점근적 상한을 제공해준다고 했다.
그런데, 이러한 점근적 상한은 본래 알고자하는 함수 f(n)에 대해서 정확하게 정보를 제공해주지 못한다는 한계점이 있다.
예를 들어보자, f(n) = 2n^2일 때, 이를 빅-오 표기법으로 쓴다면 f(n) = 2n^2 = O(n^2)이라고 할 수 있다.
그렇다면, 다음과 같은 예는 어떨까? f(n) = 2n일 때, 이를 빅-오 표기법으로 f(n) = 2n = O(n^2)이라고도 할 수 있다.
f(n) = 2n^2일 때와, f(n) = 2n일 때, 빅-오 표기법으로 표기하면 똑같이 O(n^2)라고 표기할 수 있는 것이다.
물론, 문제가 되지는 않지만 정확하게 f(n)에 대한 정보를 얻을 수 없어진다.
여기서, 리틀-오 표기법이 나온다.
리틀-오(o) 표기법
빅-오 표기법이 f(n) <= c g(n)를 뜻한다면, 리틀-오 표기법은 f(n) < c g(n)을 뜻한다.
즉, 방금처럼 f(n) = 2n^2인 경우에 O(n^2)라고 표기할 수 있지만, o(n^2)라고는 표기할 수 없게 된다.
마찬가지로, 리틀-오메가 표기법은 다음으로 설명할 수 있다.
리틀-오메가(ω) 표기법
빅-오메가 표기법이 f(n) >= c g(n)을 뜻한다면, 리틀-오메가 표기법은 f(n) > c g(n)을 뜻한다.
만약에, 리틀-오 표기법과 리틀-오메가 표기법이 헷갈린다면, 앞에서 제시한 그림을 합친 다음 그림을 참고하기 바란다.
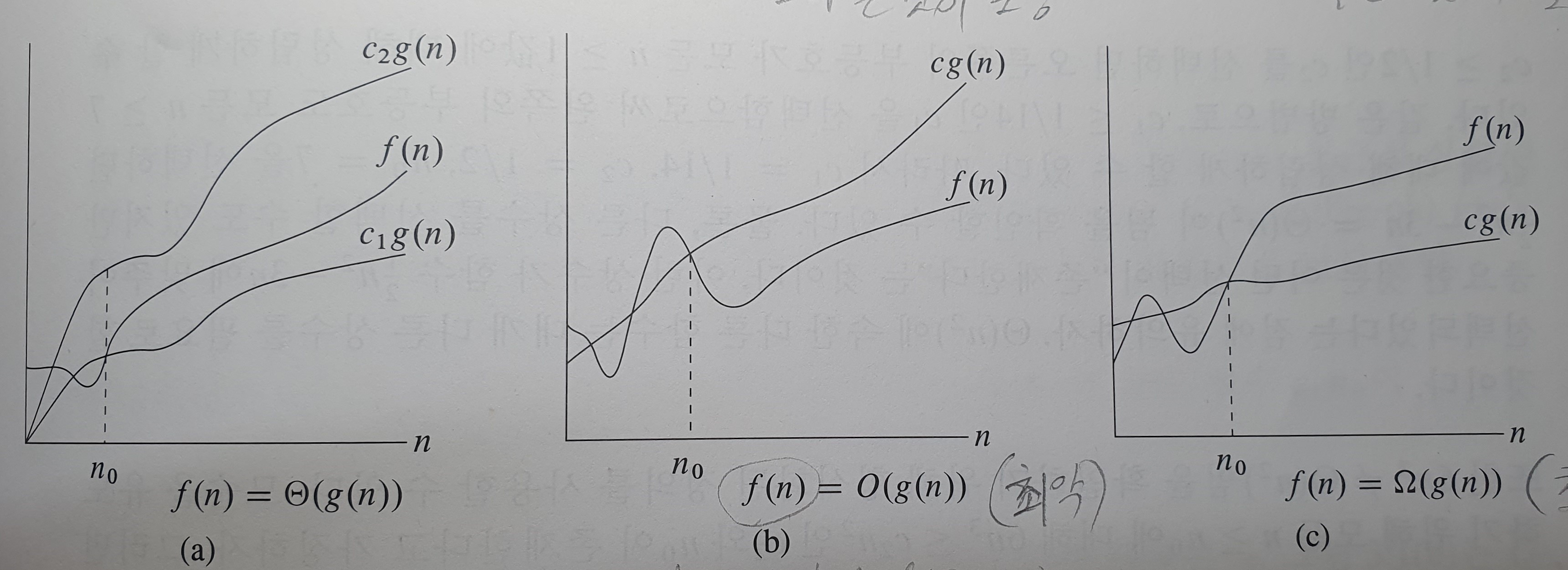
헷갈린다면, 빅-오는 f(n)에 대한 수행시간의 최악의 경우, 즉 점근적 상한을 뜻하고,
빅-오메가는 f(n)에 대한 수행시간의 최선의 경우, 즉 점근적 하한을 뜻한다고 생각하면 쉽다.
.
.
.
// 틀린 내용에 대해서, 혹은 궁금한 내용에 대한 자유로운 댓글은 언제나 환영입니다.
// 첨부한 그림은 Introduction to algorithms(third edition)에서 가져왔습니다. 문제될시 교체하겠습니다.
