
문제 정보
플랫폼 : 백준
분류 : Dynamic Programming (동적 프로그래밍)
난이도 : 실버1
링크 : https://www.acmicpc.net/problem/15991
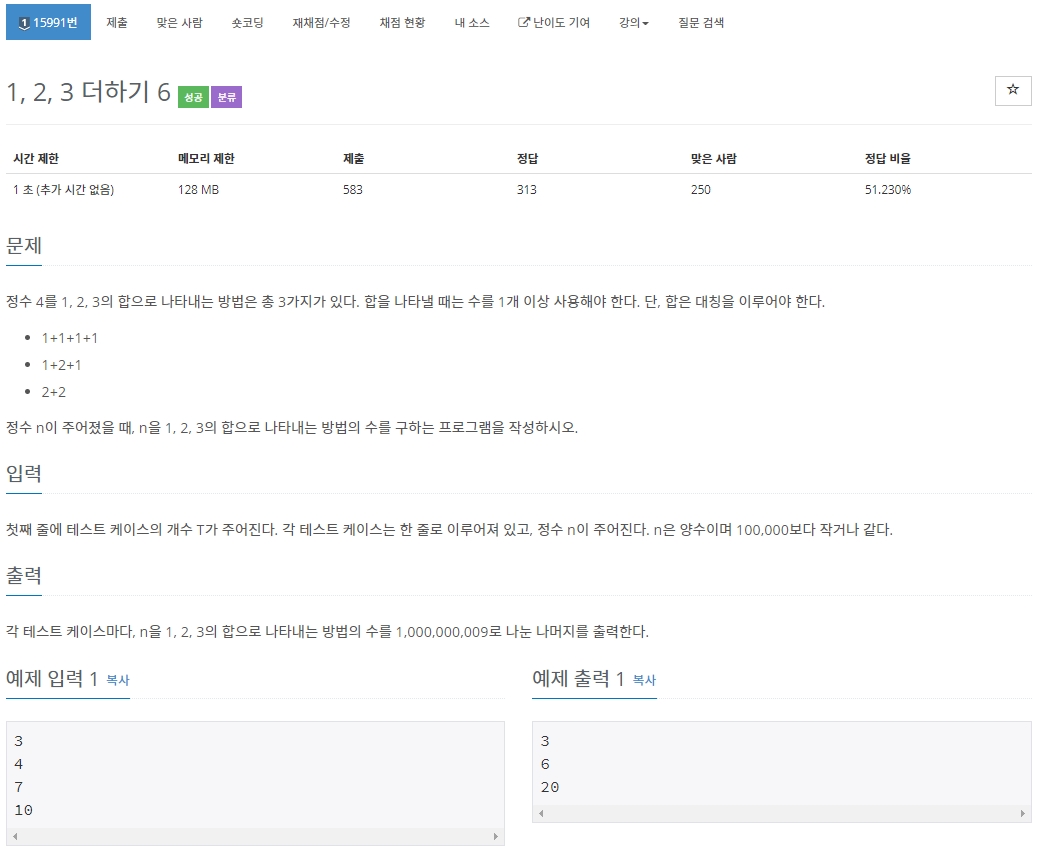
시간제한 및 메모리 제한 검증
O(n) 풀이 : 시간제한 ok
자료형 : 최대 30억, long
풀이
주말동안 Dynamic Programming 유형인 [1, 2, 3 더하기] 시리즈의 문제를 풀어봤다.
사실 어제부터 포스팅을 하려고 했는데, 머리자르느라 시간이 늦어서 쉬었다.
만약, 이전 1, 2, 3 더하기 시리즈를 풀지 않았거나, 풀이를 보지 않았다면 이곳을 클릭하여 이전 풀이를 먼저 보고오자!
점화식
dp[i] = (dp[i-2] + dp[i-4] + dp[i-6]) % 1_000_000_009;(n >= 7)
처음엔 문제를 접근하기가 어려웠다. 어떻게 대칭을 맞춰야 하는지.
30분정도 고민하자, 다음과 같은 결론이 나왔다.
대칭을 만들 수 있는 경우는
1) 1 + 대칭인 수 + 1
2) 2 + 대칭인 수 + 2
3) 3 + 대칭인 수 + 3
세 가지 경우가 있다.
1) 에서 dp[i-2]
2) 에서 dp[i-4]
3) 에서 dp[i-6]이 유도됐다!
단, 조심할 것이 있다.
4를 만드는 과정에서는, 점화식대로면 dp[2], dp[0], dp[-2]가 사용된다.
dp[n]에서 n <= 0 인 경우를 예외처리해준다 해도, 틀린 답이 나온다.
이유는 아래와 같다.
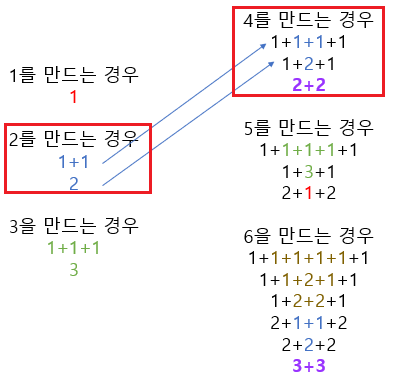
4를 만드는 과정에서, 2+2라는 특수한 상황이 생겼기 때문이다.
이제, 5를 만드는 과정을 보자.
5를 만드는 과정에서는, 점화식대로면 dp[3], dp[1], dp[-1]가 사용된다.
dp[n]에서 n <= 0 인 경우를 예외처리해주면 문제 없다.
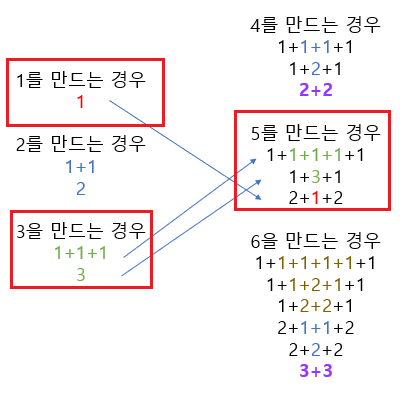
마지막으로, 6을 만드는 과정을 보자.
6을 만드는 과정에서는, 점화식대로면 dp[4], dp[2], dp[0]가 사용된다.
dp[n]에서 n <= 0 인 경우를 예외처리해준다 해도, 틀린 답이 나온다.
이유는 아래와 같다.
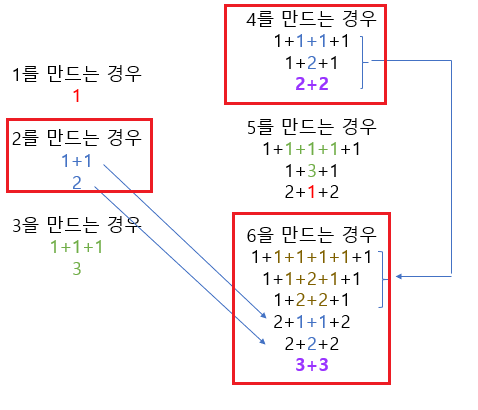
6을 만드는 과정에서, 3+3라는 특수한 상황이 생겼기 때문이다.
[점화식 설명]
점화식 설명은 상단에 적혀있고, n >= 7부터는 4 (2+2), 6(3+3)과 같은 특수한 상황이 생기지 않기 때문에, 문제없이 작동한다.
위와 같은 과정을 통해
dp[i] = (dp[i-2] + dp[i-4] + dp[i-6]) % 1_000_000_009;(n >= 7)라는 점화식이 나온다. 1 <= n <= 6 범위 까지는 직접 구해서 적어주고, 7부터는 점화식을 통해 답을 구하자.
모듈러가 나오는 이유는, 10억9로 나누어 출력하라는 제한사항이 있기 때문이다. 마지막에 모듈러를 넣는 것이 아니라, 계산 과정 중간에 모듈러를 넣는 이유는 이곳을 참조하자.
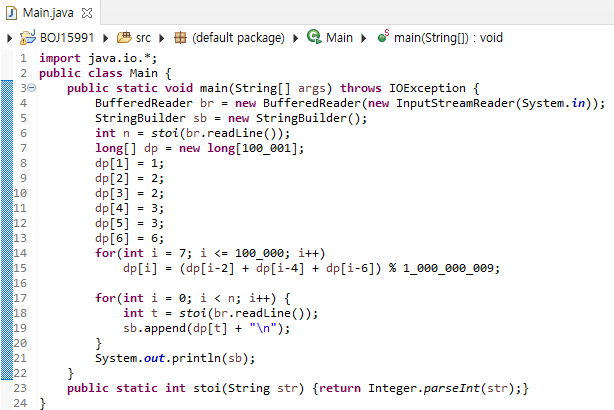
코드
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = stoi(br.readLine());
long[] dp = new long[100_001];
dp[1] = 1;
dp[2] = 2;
dp[3] = 2;
dp[4] = 3;
dp[5] = 3;
dp[6] = 6;
for(int i = 7; i <= 100_000; i++)
dp[i] = (dp[i-2] + dp[i-4] + dp[i-6]) % 1_000_000_009;
for(int i = 0; i < n; i++) {
int t = stoi(br.readLine());
sb.append(dp[t] + "\n");
}
System.out.println(sb);
}
public static int stoi(String str) {return Integer.parseInt(str);}
}
더 많은 정답 코드
블로그를 쓰기 이전에 풀어본 문제들이 많다. 해설강의는 없지만, 백준 문제의 풀이 코드가 필요한 경우 이곳을 클릭하여 소스코드를 참조해보도록 하자. 단, 코드만 복사-붙여넣기 하는것은 본인에게 결코 도움이 되지 않는다. 반드시 먼저 생각해보고, 막히는 경우에 참고하고 왜 이렇게 코드가 작성됐는지를 다시 한 번 생각해보는 습관을 들이자.
