[알고리즘] 백준 2138 전구와 스위치 Java

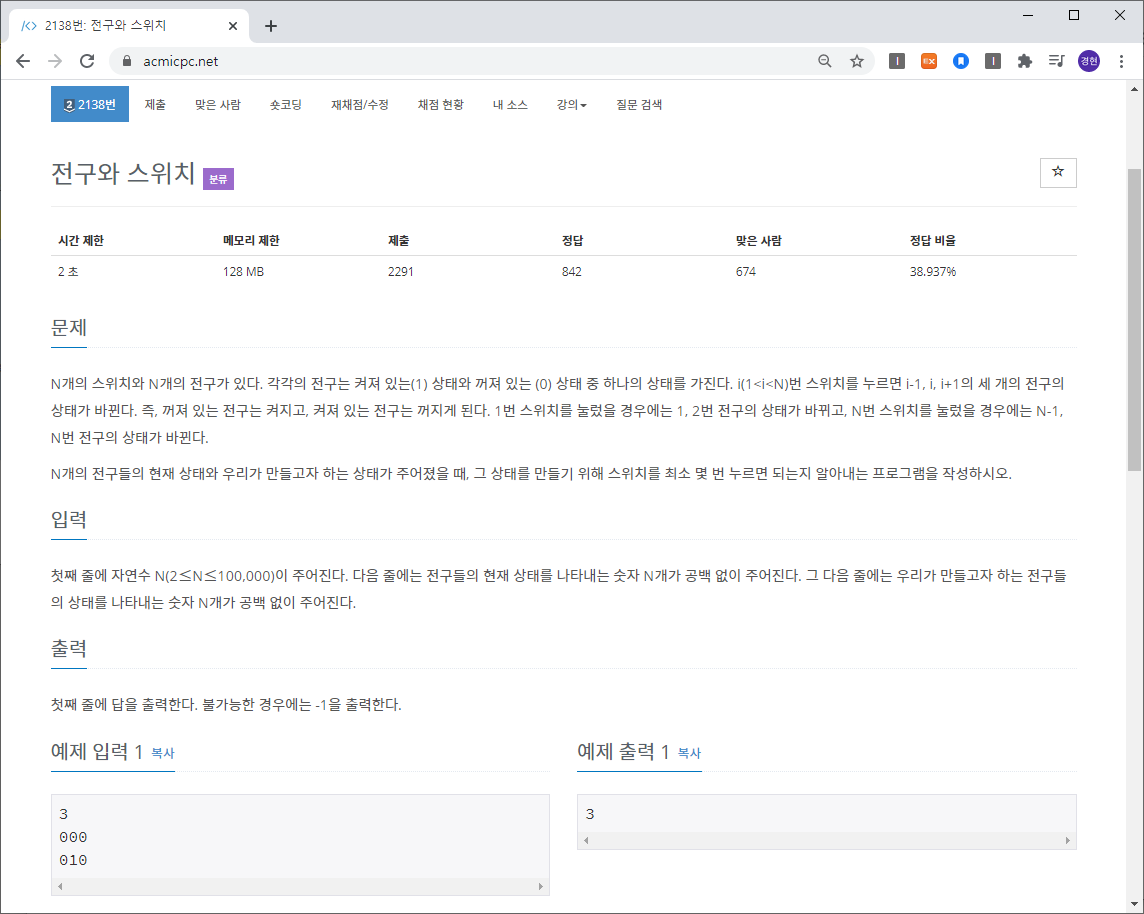
문제 정보

플랫폼 : 백준
분류 : 그리디 알고리즘
난이도 : 실버2
링크 : https://www.acmicpc.net/problem/2138

풀이

본인은 그리디 알고리즘과 DP에 약하다... 풀이를 쓰려면 내가 먼저 이해해야 하기 때문에, 문제를 먼저 풀어봤다.
3번의 실패 끝내 정답을 맞혔다. 알고보니 별거 아닌걸로 틀렸지만.. 항상 별거 아닌걸로 틀리는게 문제다! ㅠ

문제의 풀이과정은 다음과 같다.
1. 첫 번째 전구를 키는 경우와, 키지 않는 경우로 나눈다.
2. 2번째 전구 ~ n번째 전구까지 반복하면서, i-1번째 인덱스의 현재값 != i-1번째 인덱스의 기댓값이면 스위치를 켠다.
3. 1번의 두 가지 경우 모두 불가능하면 -1을 출력하고, 아니라면 두개중 최솟값을 출력한다.

예시이다. Input 데이터는

7
0010100
0111010

이다.
2번째 전구(idx: 1)를 보자.
킨 경우의 i-1 (idx: 0)와 기댓값이 다르다.
안킨 경우의 i-1 (idx: 0)와 기댓값이 같다.
3번째 전구(idx: 2)를 보자.
킨 경우의 i-1 (idx: 1)와 기댓값이 다르다.
안킨 경우의 i-1 (idx: 1)와 기댓값이 다르다.

4번째 전구(idx: 3)를 보자.
킨 경우의 i-1 (idx: 2)와 기댓값이 같다.
안킨 경우의 i-1 (idx: 2)와 기댓값이 다르다.
5번째 전구(idx: 4)를 보자.
킨 경우의 i-1 (idx: 3)와 기댓값이 같다.
안킨 경우의 i-1 (idx: 3)와 기댓값이 다르다.
6번째 전구(idx: 5)를 보자.
킨 경우의 i-1 (idx: 4)와 기댓값이 다르다.
안킨 경우의 i-1 (idx: 4)와 기댓값이 다르다.
마지막 전구(idx: 6)를 보자.
킨 경우의 i-1 (idx: 5)와 기댓값이 같다.
안킨 경우의 i-1 (idx: 5)와 기댓값이 다르다.모든 작업이 완료됐다. 이제 n번째 전구 (idx: 6)을 비교해보자. 킨 경우는 기댓값과 다르므로 정답이 아니다. 키지 않은 경우는 기댓값과 같으므로, 정답은 5이다.
일반화시켜 코드로 작성해보자.
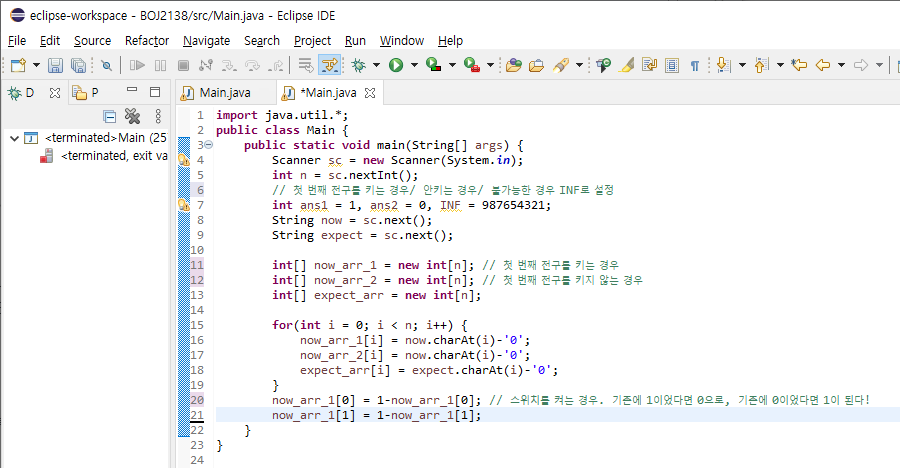입력을 받자. 입력 예시를 보면, 각 전구의 상태가 띄어쓰기로 구분되는 것이 아니라 붙어있다. 따라서 입력을 String으로 받고, 한 글자씩 떼서 배열에 넣어준다.
그리고, 첫 번째 전구를 키는 경우 (now_arr_1), 키지 않는 경우(now_arr_2)로 나눠서 선언해준다. ans1 = 1인 이유는 첫 번째 전구를 이미 켰기 때문이다.
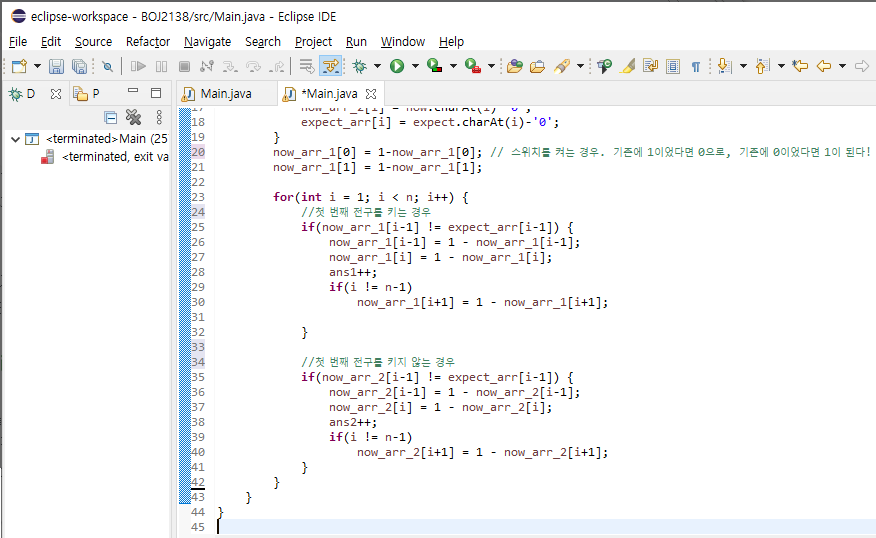이후에, i = 2번째 전구 ~ n번째 전구까지 i-1 번째 전구가 기댓값과 다르면 스위치를 눌러주는 작업을 구현해주자.
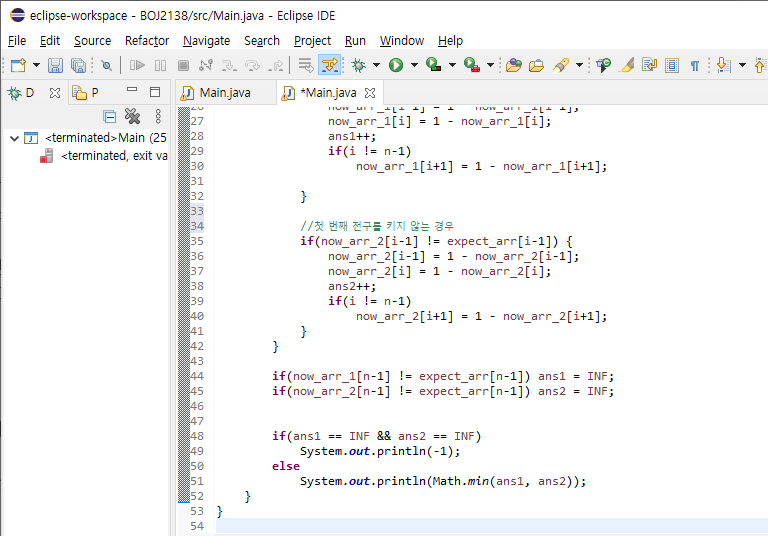마지막으로, n번째 전구가 기댓값과 다르면 INF로 설정해준다. ans1과 ans2가 모두 INF이면 첫 번째 전구의 스위치 여부에 관계 없이 불가능한 경우이다. 그 이외에는 두개중 최솟값을 출력해주자.

코드

import java.util.*;
public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int ans1 = 1, ans2 = 0, INF = 987654321;
		String now = sc.next();
		String expect = sc.next();
		
		int[] now_arr_1 = new int[n];
		int[] now_arr_2 = new int[n];
		int[] expect_arr = new int[n];
		
		for(int i = 0; i < n; i++) {
			now_arr_1[i] = now.charAt(i)-'0';
			now_arr_2[i] = now.charAt(i)-'0';
			expect_arr[i] = expect.charAt(i)-'0';
		}
		now_arr_1[0] = 1-now_arr_1[0];
		now_arr_1[1] = 1-now_arr_1[1];
				
		for(int i = 1; i < n; i++) {
			if(now_arr_1[i-1] != expect_arr[i-1]) {
				now_arr_1[i-1] = 1 - now_arr_1[i-1];
				now_arr_1[i] = 1 - now_arr_1[i];
				ans1++;
				if(i != n-1)
					now_arr_1[i+1] = 1 - now_arr_1[i+1];						
				
			}
			if(now_arr_2[i-1] != expect_arr[i-1]) {
				now_arr_2[i-1] = 1 - now_arr_2[i-1];
				now_arr_2[i] = 1 - now_arr_2[i];
				ans2++;
				if(i != n-1)
					now_arr_2[i+1] = 1 - now_arr_2[i+1];		
			}
		}

		if(now_arr_1[n-1] != expect_arr[n-1]) ans1 = INF;
		if(now_arr_2[n-1] != expect_arr[n-1]) ans2 = INF;
		
		
		if(ans1 == INF && ans2 == INF)
			System.out.println(-1);
		else
			System.out.println(Math.min(ans1, ans2));
	}
}

더 많은 정답 코드

블로그를 쓰기 이전에 풀어본 문제들이 많다. 해설강의는 없지만, 백준 문제의 풀이 코드가 필요한 경우 이곳을 클릭하여 소스코드를 참조해보도록 하자. 단, 코드만 복사-붙여넣기 하는것은 본인에게 결코 도움이 되지 않는다. 반드시 먼저 생각해보고, 막히는 경우에 참고하고 왜 이렇게 코드가 작성됐는지를 다시 한 번 생각해보는 습관을 들이자.