[알고스팟] 게임판 덮기

게임판 덮기

풀이

완전탐색 문제이다.
문제는 추상화, 정규화 능력을 필요로 한다.
시행을 하는 방법을 본인이 일정하게 정해야 한다.
블록을 어떻게 어디서부터 놓아야 할지를 정해야 한다.

다행인 것은 블록의 구분이 없다는 것이다.
즉 블록이 채워진 모양만 같으면
어디에 어떤 블록을 놓을지는 중요하지 않다.
따라서 우리는 순서를 강제할 수 있다.
일관적인 풀이를 위해서이다.

순서는 일반적으로 왼쪽 위에서부터 시작한다.
추가적으로 내가 신경 써야 하는 부분을 좁힐 수록 오류가 생길 위험이 적다.
(컴퓨터는 실수나 거짓말을 하지 않는다.)
그래서 나는 칸 하나만 신경 쓰기로 한다.

칸 하나에서 놓을 수 있는 블록의 모양은 네 가지이다.

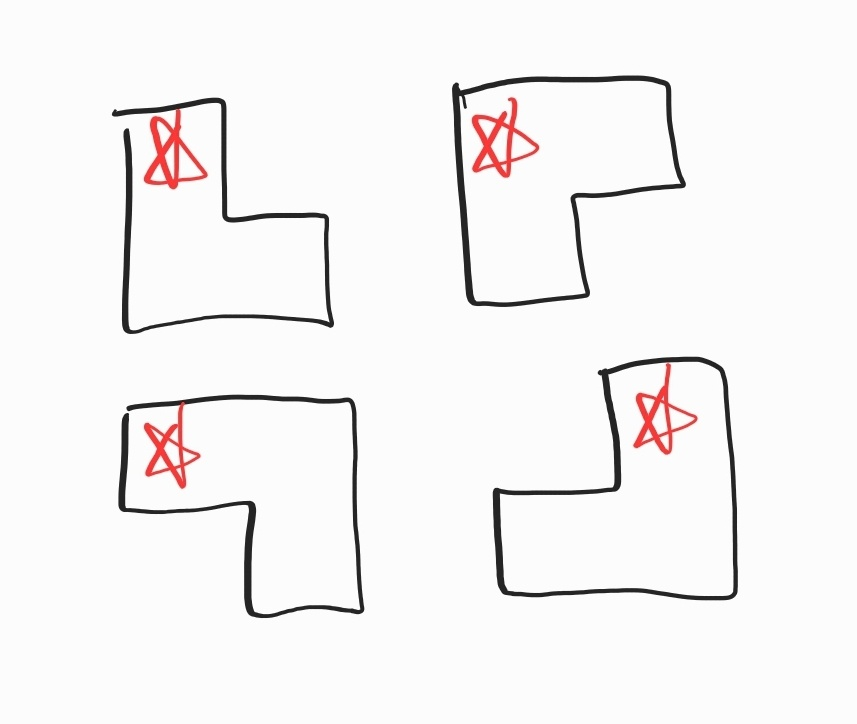
이렇게 네 가지로 줄어든 이유는 내가 왼쪽 위에서부터 블록을 하나씩만 보고 있기 때문이다.

내가 보고 있는 블록을 포함하되,
그 블록의 왼쪽과 위쪽은 포함해선 안 된다. 왜냐하면 그곳은 이미 본 곳이기 때문이다.
따라서 나는 왼쪽 위부터 훑으며 위의 네 가지 블록을 놓을 수 있는지 여부를 고려해주기만 하면 된다.

최단 거리 문제가 아니라 경우의 수를 세는, 어차피 모두 다 가봐야 하는 문제이므로 dfs를 이용한다.
dfs를 이용하면 변수를 복사할 필요가 없다는 장점이 있다.

코드를 보자.

코드

import sys


scan = sys.stdin.readline
blocks = [[(1, 0), (1, 1)], [(1, 0), (1, -1)], [(0, 1), (1, 1)], [(0, 1), (1, 0)]]


def solution():
    T = int(scan())

    for t in range(T):
        tc()


def tc():
    def is_valid(i, j):
        return 0 <= i < H and 0 <= j < W

    def fill(to_fill, what):
        for y, x in to_fill:
            board[y][x] = what

    def dfs(i, j, white_left):
        while True:
            if j >= W:
                i += 1
                j = 0
                if i >= H:
                    if white_left == 0:
                        return 1
                    else:
                        return 0
                    
            if board[i][j] == '.':
                break
            j += 1

        cnt = 0
        for to_fill in blocks:
            to_fill = [(y, x) for y, x in [(i + dy, j + dx) for dy, dx in to_fill + [(0, 0)] ] if is_valid(y, x) and board[y][x] == '.']
            if len(to_fill) == 3:
                fill(to_fill, '#')
                cnt += dfs(i, j + 1, white_left - len(to_fill))
                fill(to_fill, '.')

        return cnt

    H, W = map(int, scan().split())
    board = [list(scan().strip()) for _ in range(H)]
    white = sum([sum([board[y][x] == '.' for x in range(W)]) for y in range(H)])

    if white % 3 == 0:
        answer = dfs(0, 0, white)
    else:
        answer = 0

    sys.stdout.write("%d\n" % answer)


solution()

dfs(i, j, white_left) 함수는 white_left만큼의 흰색 칸이 남았을 때
(i, j) 부터 시작해서 블록을 채울 수 있는 경우의 수를 반환한다.

함수가 호출되면 (i, j)에서 가장 가까운 흰색 칸을 찾는다.
j를 증가시키다가, j가 W를 넘어가게 되면 j를 0으로 하고 i를 1 증가시킨다.
이는 밑으로 한 칸 내려가서 다시 왼쪽부터 보는 것을 뜻한다.
i가 H와 같다는 것은 게임판을 다 보았다는 뜻이다.
다 보았을 때 만약 흰색 칸이 남아있지 않다면
이는 흰색 칸을 모두 채우는 데 성공했다는 뜻이다.
따라서 1을 반환한다.
이 값은 이 함수가 재귀호출된 함수에서 사용될 것이다.

이후에는 현 위치에서 블록들을 점검하면서 재귀호출을 한다.
dfs의 장점인 복사를 안 해도 되는 점을 이용한다.
재귀호출 이전에 블록을 표시해주고 호출 이후에 표시했던 것을 다시 복구하면 된다.

마지막에 결과값을 호출해주면 된다.

시간복잡도

완전탐색은 보통 $O(N^m)$의 시간복잡도를 가진다.
$N$은 선택의 가지수, $m$은 선택해야 하는 수이다.
여기서 $N=4, \ m=16$이다. ($m$ = 흰색 칸 수 // 3이며, 흰색 칸 수는 3으로 나누어 떨어져야 한다)
$4^{16}$은 아주 큰 수라서 불가능할 것 같지만
현실적으로는 이것보다 아주 작다.
왜냐하면 블록을 쌓으면서 밑이나 오른쪽을 방해하기 때문이다.
그래서 이 문제를 완전탐색으로 풀 수 있다.