[알고스팟] 폴리오미노

풀이

다른 dp들이 많이 그렇듯
n=1인 사각형에 하나씩 추가해가면서
경우의 수를 더해가는 문제라고 생각을 했다.
일단 같은 폴리오미노 (회전하여 같아지는) 에 대한 정의도 없고 그래서
이 방법은 통하지 않는 거 같다.
어디다 붙일지에 대한 방법도 매번 달라져서 더 복잡해진다.

책을 보면 위에서부터 한줄 한줄 세어 간다.
가로로는 단조일 필요는 없으니까
각 줄이 세로로 붙어있으면 된다.
나는 남은 사각형의 개수와 현재 줄에 세로로 쌓으려는 사각형의 개수만 알면 된다.

동적 계획법에서 가장 중요한...
이전의 과정을 보지 않는 것이다.

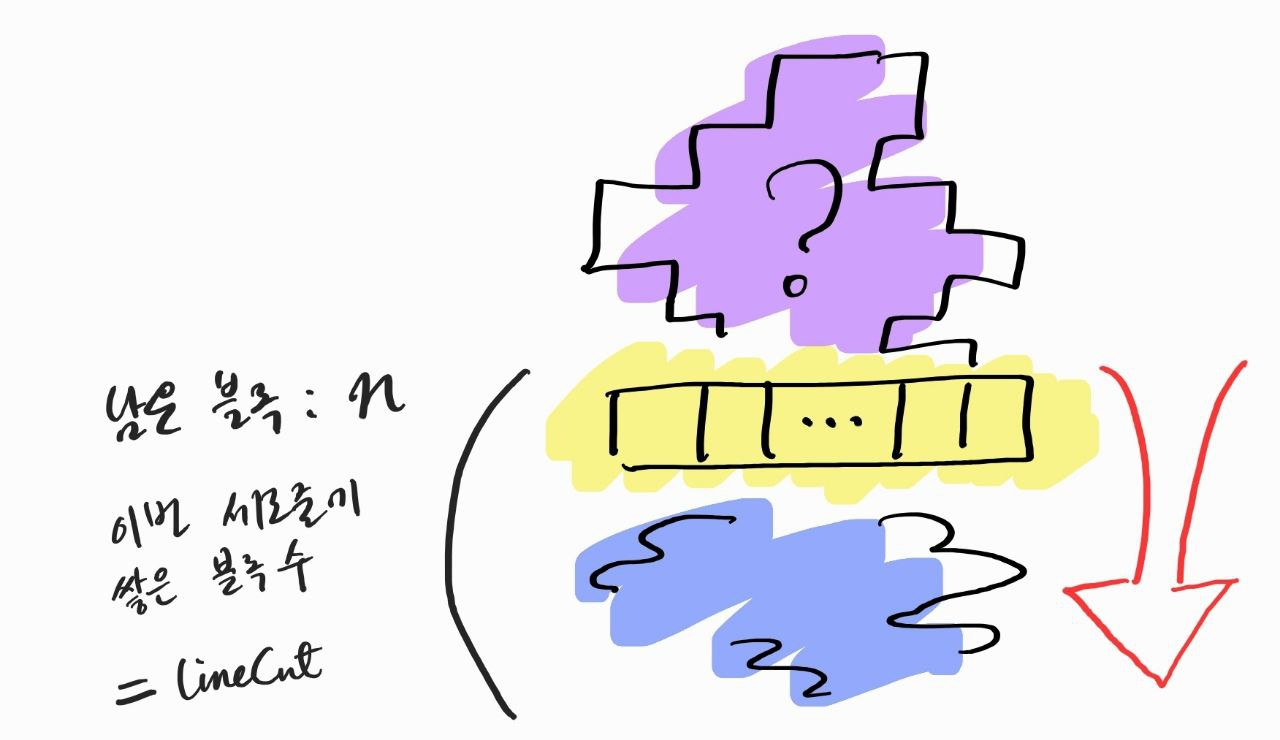
위 그림에서 보라색 부분(과거)은 중요치 않다.
내가 알고 싶은 것은 노란색과
바로 다음 파란색이다.
정확히는 노란색에서 파란색으로 어떻게 나아갈지다.

현재 남은 블록을 n, 이번 세로줄에 쌓은 블록 수를 lineCnt 라고 한다.

그렇다면 다음 세로줄을 어떻게 쌓을지를 알아보아야 한다.

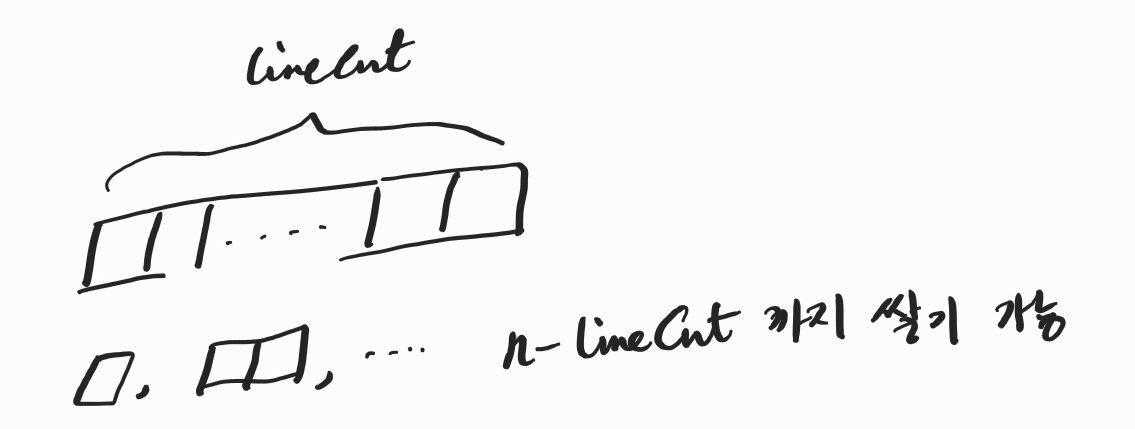
내가 이번 세로줄에 lineCnt만큼 쌓는다면
총 블록은 n - lineCnt만큼 남았을 것이다.
즉 다음 줄에는 1개부터 n - lineCnt개까지 쌓을 수 있다.

이제 경우의 수를 구해보자.

경우의 수는 계속 곱해나가야 한다.
왜? 이것은 따지고 보면 순열이기 때문이다.
그렇다면 이번 세로줄과 다음 세로줄 사이엔 어떤 관계가 있을까?

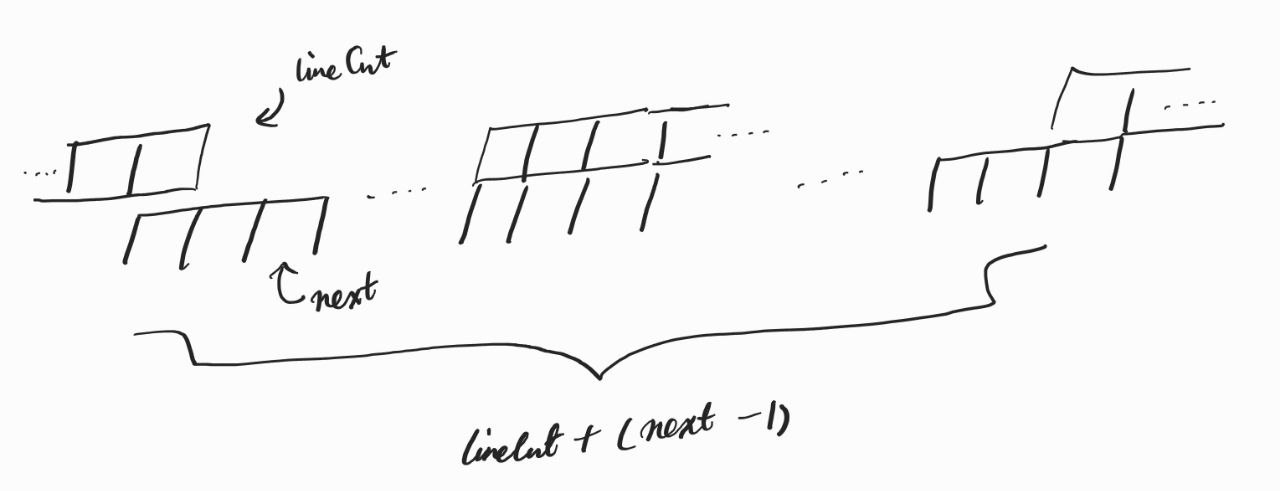
이번 세로줄에 쌓을 블록 수를 lineCnt, 다음 세로줄에 쌓을 블록 수를 next라고 했을 때
둘의 관계는 위의 그림과 같이 정리된다.

다음 세로줄의 왼쪽 끝 블록에
위 세로줄을 오른쪽 끝부터 왼쪽 끝까지 차차 맞춘다고 하자.
그러면 당연히 lineCnt만큼 갔을 것이다.
그러나 여기서 오른쪽으로 next - 1만큼 더 갈 수 있다.
그래서 위에 lineCnt, 밑에 next 개가 있다고 할 때
발생할 수 있는 경우의 수는 lineCnt + next - 1이다.

결과적으로, 경우의 수는
next를 1부터 n - lineCnt까지 늘려가며
(lineCnt + next - 1) * next의 경우의 수를 다 더하는 것과 같다.

코드

#include <cstdio>
#include <cstring>

#define MAX 100
#define DIV 10000000

void tc();

int main() {
    int C;
    scanf(" %d\n", &C);
    for (int i = 0; i < C; i++) {
        tc();
    }
    return 0;
}

int dp[MAX + 1][MAX + 1];

int poly(int n, int lineCnt) {
    if (n - lineCnt == 0) return (dp[n][lineCnt] = 1);
    int &ret = dp[n][lineCnt];
    if (ret == -1) {
        ret = 0;
        for (int nextCnt = 1; nextCnt <= n - lineCnt; ++nextCnt) {
            int cases = lineCnt == 0 ? 1 : lineCnt + nextCnt - 1;
            cases = (cases * poly(n - lineCnt, nextCnt)) % DIV;
            ret = (ret + cases) % DIV;
        }
    }
    return ret;
}

void tc() {
    int n;
    scanf(" %d", &n);
    memset(dp, -1, sizeof(dp));
    printf("%d\n", poly(n, 0));
}