회귀 분석

회귀 분석

상관 분석을 통해 인과 관계는 알 수 없다.
이를 알아보는 것이 회귀 분석이다.

회귀 분석은 관찰된 연속형 변수들에 대해 변수들 사이의 모형을 구한 뒤 적합도를 측정해 내는 분석 방법이다.

회귀 분석은 두 변수의 관계를 설명하고 예측할 수 있다.

$y = ax + b$라고 했을 때 $x$는 독립, $y$는 종속변수이다.
여기서 기울기인 $a$와 절편인 $b$를 알아내는 것이 목표이다.

단순 선형 회귀분석

독립변수가 하나일 때이다.

아버지와 아들의 키의 관계를 산점도로 나타내었다. 여기서 선형 회귀분석을 한다고 치자. 선형 회귀분석을 하려면 관계를 어떤 함수로 표현해야 하는데, 함수는 하나의 $x$값은 하나의 $y$ 값을 가진다. 하지만 그래프는 그렇지 않다. 그래서 이 산점도를 그나마 잘 표현하는 직선 하나를 그어야 한다. 이렇게 되면 오차가 존재한다. 그 선을 지나가지 않는 점들이 모두 오차이다.

오차를 수치로 나타내는 식은 여러 가지가 있다. 이른바 최소 제곱법은 오차의 제곱의 합을 구하는 방식이다. 실제 결과를 $y_i$, 예측값을 $\hat y_i$라고 했을 때 최소 제곱법으로 구한 오차는 다음 식으로 구할 수 있다.

기울기

$x_i$에 매핑되는 $y_i$의 추정치 $\hat y_i = \hat \alpha - \hat \beta x_i$이다. 이때 절편인 $\hat \alpha$와 기울기인 $\hat \beta$의 식은 다음과 같다.

(기울기는 피어슨 상관계수랑 식이 비슷하다. y쪽의 분산으로 안 나눠주면 된다.)

단순 선형 회귀분석을 하기 위해서는

1. $\bar x$와 $\bar y$를 구한다. (좌표에서 모든 x, y값을 각각 더해서 n으로 나누면 된다.)
2. 기울기 $\hat \beta$을 구한다. 기울기는 상관계수이다. 공분산을 x의 표준편차로 나눈다.
3. 절편 $\hat \alpha$을 구한다.

가설

$H_0$(귀무 가설): X변수들은 Y변수들과 선형 관계가 없음
$H_1$(대립 가설): X변수들은 Y변수들과 선형 관계가 있음

F검정을 통해 기울기가 존재하는지 검정(통계적 유의성)하고 $H_0$의 참 거짓을 가린다.

만약 관계가 있다고 밝혀진다면, $H_0$이 거짓이라면 T검정을 통해 각 변수의 영향력을 확인할 수 있다.

단순 선형 회귀에서 F분포 = T분포이다.

선형회귀의 가정

선형성

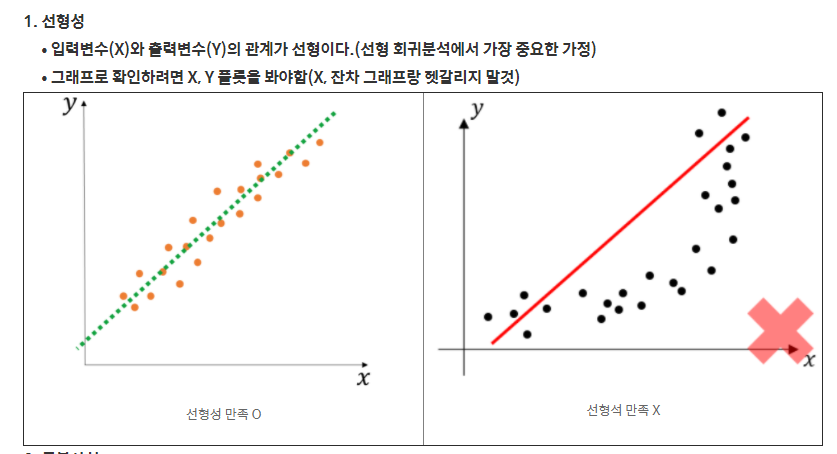
종속변수 Y는 독립변수 X에 대해 선형적인 관계를 갖는다.
만족하지 않는다면 데이터를 변환하거나, 독립 변수에 지수승을 붙인다.

정규성

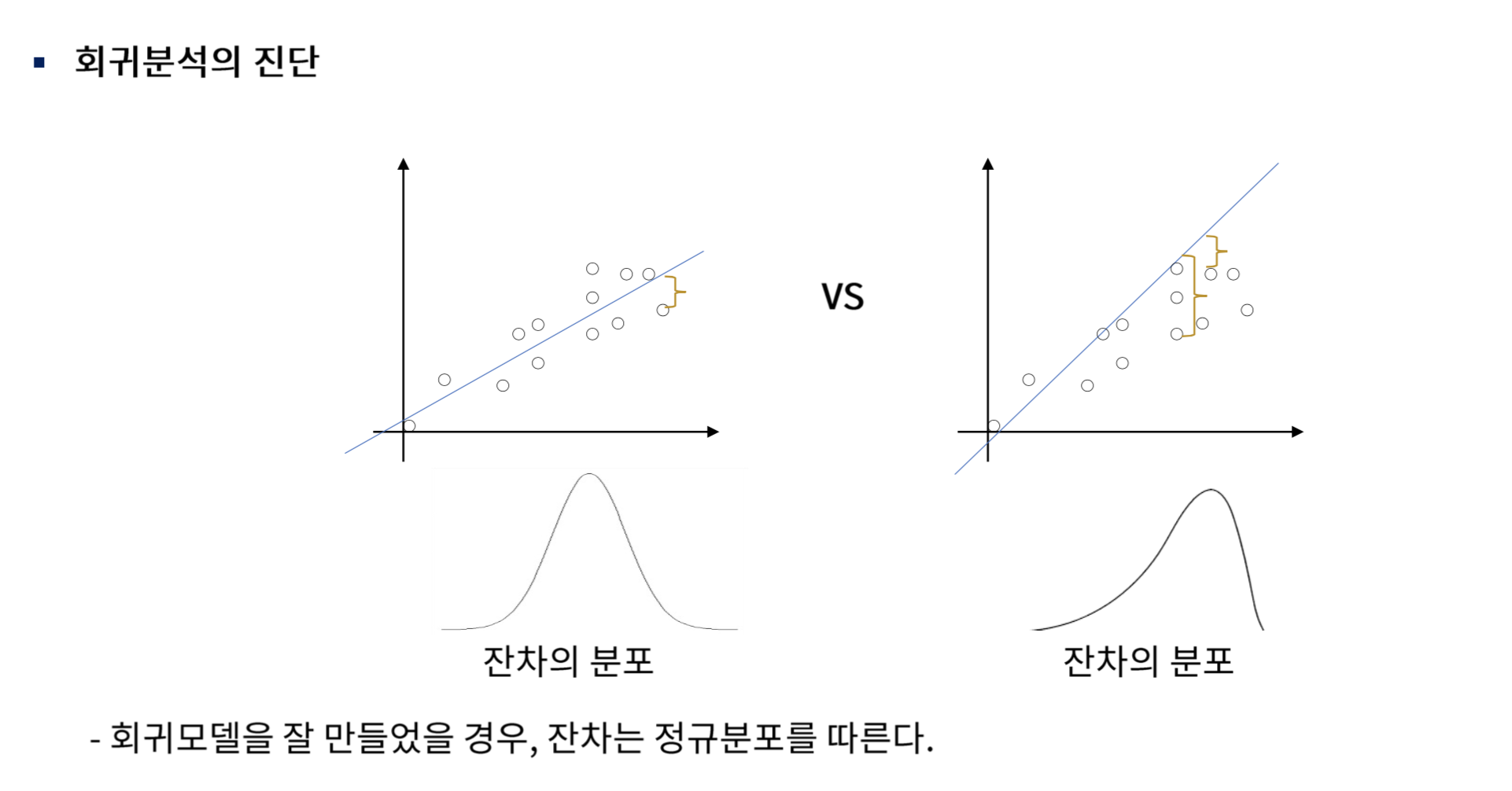
오차는 모두 평균이 0이고 분산이 $\sigma^2$인 정규분포다.
이게 성립을 해야만 F검정으로 가설 검정을 할 수 있다.
산점도, 히스토그램, Q-Q plot을 통해 정규성을 검토할 수 있다.

결과를 또 다른 함수(logit, inverse, log 등)에 넣어서 데이터를 변환하는 방식으로 해결할 수 있다.

등분산성

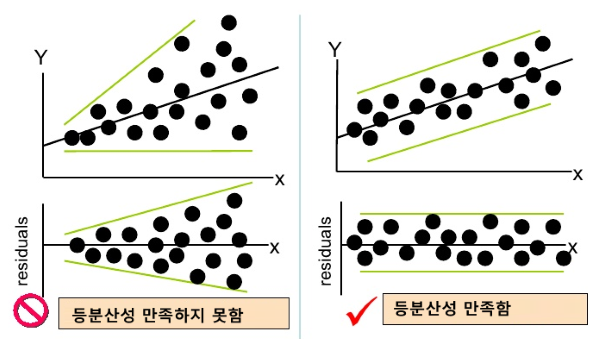
오차항의 확률분포의 분산은 모든 X에 대해 일정한 상수이다.
이게 성립하지 않으면 F, T검정을 사용할 수 없다.

독립성

(이렇게 오차가 쏠려있으면 안 된다.)

오차는 random variable (경향성이 없음)로서 독립적이며 동일하게 분포하는 확률 분포이다.
이게 성립 안 하면 회귀식이 틀렸거나 중요한 설명 변수가 누락됐다는 뜻이다.

혹은 다중공선성이 있을 수도 있다. 예를 들어 어떤 두 변수가 독립이 아니라 서로 연관이 되어 있다는 뜻이다. $x_1 = 2x_2$ 같은 관계를 가질 수 있다. 이는 제거를 해야 하는데 성능이 좋으면 안 해도 된다.

Durbin-Watson 통계량으로 확인할 수 있다.

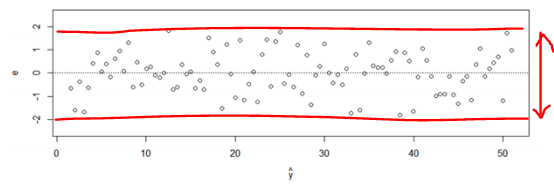
위 네 개 가정이 성립해서 잘 맞는 회귀 분석의 잔차들은 아래와 같은 그래프를 그린다.

선형회귀 시 이슈

outliers

잔차(오차)가 다른 대부분의 것보다 큰 경우

해결법
제거하거나 데이터를 변환한다.
Robust regression
Quantile regression

다중공선성

독립변수 간에 강한 상관관계가 있는 경우
상관 분석이나 Variance Inflation Factor로 확인한다.

해결법
Feature Engineering
Regularization (Ridge, LASSO, ElasticNet)

Ridge는 가중치 조절, LASSO는 그런 변수를 삭제, ElasticNet은 둘 다 사용한다.

선형회귀모델 평가

$R^2$, 결정계수

변수간 영향을 주는 정도 또는 인과관계의 정도를 정량화 해서 나타낸 수치이다.
추정한 선형의 모형이 주어진 자료에 대해 얼마나 적합한가를 나타낸다.

이상치

이상치는 독립변수, 종속변수에서 나올 수 있다.

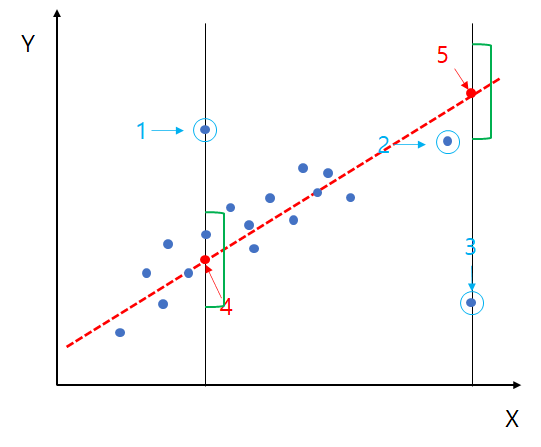
영향점: 모든 데이터와 이상치 제거한 데이터의 회귀 분석 결과가 클 때, 이상치는 영향점이 된다.