다음은 < Deep Learning with Pytorch Step by Step > by Daniel Voigt Godoy 를 참고하여 번역한 내용입니다. 주관적인 해석이 섞여있습니다.

autograd

pytorch의 Automatic differentiation(Gradient) package이다. 이 친구가 하는일은, neural net이 backpropagate할 때 필요한 gradient 계산들 (partial derivatives, chain rule .etc)을 대신 해준다.

autograd 패키지 안의 attribute를 찬찬히 살펴보자

.backward()

그래서, 어떻게 pytorch가 모든 gradient를 계산할 수 있는가 하면, 그것들은 .backward() 메소드 덕분이다. Require_grad=True로 설정된 모든 텐서들에 대해 gradient를 계산한다.

backpropagation에서 gradient를 계산하는 첫 starting point가 되는 값이 loss 값임을 알고 있을 것이다. 그리고 우리는 이 loss값을 모든 가중치들(parameters; weight and bias)에 대해서(with respect to) 미분을 계산하게 된다.

그렇므로, 이 .backward() 메소드는 gradient 계산이 시작되는 지점인 loss 변수에 적용해주어야 한다. 이렇게: loss.backward()

간단한 Neural Net을 만들어보면,

##simple NN##

#step 1: forward pass
y_hat = b + w * x_train

#step 2: loss 값 계산 (loss function: MSE)
error = y_train - y_hat
loss = (error**2).mean()

#step 3: b와 w에 대한 gradient 계산
b_grad = -2 * error.mean()
w_grad = -2 * (x_train * error).mean()
#이렇게 계산할 수도 있지만, 아까 배웠던 backward()를 써보면
loss.backward()

그렇다면 이 loss.backward()가 컨트롤하는 변수는 어떤 것이 있을까?
일단, b,w에 대해 requires_grad = True로 설정했기 때문에 이 backward() 메소드가 이 두 가중치에 대해서 예의주시하고 있을 것이다! (b,w는 gradient가 require하다고 했으니까, 얘들은 신경써준다는 말이다.)
그리고, 이 b,w로 우리가 무엇을 계산했었는지 떠올려보자. 그렇다. 이 모델의 목표인 y_hat이다. b,w를 통해 y_hat을 만들기 때문에, backward() 메소드가 b,w를 예의주시하는 것은 곧, y_hat을 예의주시하게 됨을 의미한다. 그 다음에, 이 y_hat은 어떤 것을 만들어 내는지 생각해보자. 바로, error값이다 (error = y_train -y_hat). 그러므로, backward() 메소드는 error까지 관심범위에 넣게 된다.

이해를 쉽게 하기 위해, ''예의 주시'', ''관심 범위''로 표현했는데, 이러한 추상적인 단어들은 pytorch의 Dynamic Computational Graph의 개념을 비유해서 설명한 것이다.
backward() 메소드는 gradient를 구하려고 하는 변수들 (requires_grad = True로 인자를 전달한 변수들)에 대해 DCG에 차곡 차곡 neural net의 계산 흐름을 쌓게 된다.

'그' chain rule과 같은 개념이라고 생각하면 된다. forward pass에서, (b, w) -> y_hat -> error의 흐름으로 갔으니, chain rule에 따르면, loss.backward()를 call했을 때, loss -> error -> y_hat -> b,w 의 graph가 만들어지는 것을 상상할 수 있을 것이다.

여기서, x_train, y_train은 DCG에 포함 되지 않는다는 것을 명심하자. 우리는 requires_grad=False로 설정한다.

.grad

위에서 .backward()를 통해 gradient를 계산한다는 것은 알았다. 이때, 계산한 gradient의 실제값 또한 확인할 수 있다.

b.grad, w.grad

여기서 강조할 것은, gradient들은 축적된다는 것이다.

축적이라고?

만약, 우리가 앞선 simple NN 코드를 한번 더 실행하게 되면 (총 두번 실행시키면) 어떤 일이 벌어질까?

#첫 번째 실행
tensor([-3.3881],tensor([-1.9439])
#두 번쨰 실행
tensor([-6.7762],tensor([-3.8878])

gradient 값이 정확하게 두 배가 된 것을 알 수 있다!! 이를 통해 유추할 수 있는 것은, 우리가 gradient를 어떤 container에 저장할 때, 실행 될 때마다 그 container 의 길이가 필요한 만큼 늘어나는 게 아니라, 원래 있던 변수의 자리에 맞는 원소에 += 연산이 된다는 것이다. 말이 조금 횡설 수설하는 것 같지만, 쉽게 말해 그냥, NN 모델이 실행될 때마다 원래 값에 새로운 값이 계속 더해진다는 것이다. 그리고 이게 바로 축적 (accumulate)이 의미하는 바이다.

그런데, 조금 더 생각해보면 이게 문제가 된다는 것을 알 수 있다. 우리는 현재의 loss값에 해당하는 gradient를 사용해서 parameter들을 업데이트해야되는데, gradient들이 이렇게 계속 축적되어버리면 안될 것이다. 그렇다면, 왜 pytorch는 gradient를 축적하는 것을 default로 구현해놓은 것일까?

여기서부터는 나도 이해를 잘 못했지만, circumvent harware limitation 이 있을 때 유용하기 때문이라고 한다.
엄청나게 커다란 모델을 돌릴때, mini-batch안에 필요한 데이터 포인트의 수가 너무너무 커서 우리가 가진 하드웨어 자원을 초과할 수 있다. 좋은 그래픽 카드를 살 돈이 없다면 어떻게 해야할까? Mini-batch임에도 우리의 컴퓨터에게는 너무 커다란 뭉탱이니까, 이를 sub-mini-batch로 다시 쪼개는 것이다. 이 sub-mini-batch를 계산해서, 축적한다면, full mini-batch의 gradient를 계산할 수 있게 되는 것이다. 그래서 축적이 필요한 것이다! 돈 없는 나같은 사람들에게는 참 마음 따뜻한 배려인 것이다.

zero_

앞서 말했듯, autograd에서 gradient가 축적 되기 때문에, gradient를 통해 가중치들을 업데이트할 때마다, 다음으로 넘어가기 전에 이 zero_() 메소드를 통해 gradient를 0로 만들어 줘야한다. 이렇게: b.grad.zero_()

여기서 잠깐, 메소드 이름 뒤에 _가 들어가는 것은 이유는 무엇일까?

pytorch에서, 메소드이름 뒤에 _가 들어가는 아이들은 in_place의 의미를 가지고 있다. pandas를 아는 사람들이라면 이해가 쉬울 것이다. 어떤 메소드를 적용한 결과값으로 곧바로 해당 변수를 바꾼다는 소리다. 예를 들어, 파이썬의 list.sort()를 하면 원래의 list의 값이 변하는 것과 같은 말이다.

Updating Parameters

numpy의 가중치 업데이트 코드는 충분치 않은 점이 있다. 기존의 numpy 방식대로 하면 다음과 같다.

## Use Numpy's code
#Initialize b, w randomly
torch.manual_seed(12357)
b = torch.rand(1, requires_grad = true, dtype = torch.float)
w = torch.rand(1, requires_grad = true, dtype = torch.float)

n_epochs = 1000
for epoch in range(n_epochs):
  y_hat = b + w * x_train # feed forward pass: compute prediction with given parameters; w,b
  error = y_hat-y_train 
  loss = (error ** 2).mean() #compute loss
  
  #call backward method -> compute gradients of loss w.r.t b and w
  loss.backward() 
  #update parameters
  b = b - lr * b.grad
  w = w - lr * w.grad 
  
  b.grad.zero_()
  w.grad.zero_()

이렇게 돌려보면, 다음과 같은 에러메세지가 출력된다.
>> AttributeError: 'NoneType' object has no attribute 'zero_'

에러를 살펴보면, 우리가 넘겨준 값이 None이 되어서 zero라는 attribute가 없다고 한다. `b.grad.zero 에서 zero_라는 attribute가 없다고 했으니, b.grad`가 None이 되었다는 것이다. #update paramerters 부분을 보면, b에 새로운 값을 assign해주었기 때문에, b값이 바뀌었기 때문에, 기존에 가지고 있던 grad attribute또한 없어진 것이다(우리는 새로 업데이트 된 b에 대해서 gradient를 구하지 않았다. 아직!)
정리해서 말하면, 가중치 업데이트를 진행하는 과정에서 gradient를 잃기 때문에 grad attribute는 None값이 되어 에러가 발생하는 것이다.

이번에는 조금 코드를 바꿔서 새로 돌려보자.

## Use in-place python assignment
b -= lr * b.grad
w -= lr * w.grad

b.grad.zero_()
w.grad.zero_()

>> RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.
또 에러가 발생했다! 원인은 바로 pytorch가 gradient를 계산하는 tensor나 그와 관련된 모든 파이썬 operation으로 부터 DCG(Dynamic Computational Graph)를 만들기 때문이다. 이에 대한 설명은 DCG 부분에서 더 첨언하도록 한다.

.no_grad()

불행히도, 지금까지 했던 두 방법 모두 가중치 업데이트를 실패했다. 이제 pytoch autograd의 no_grad()를 시도해볼 차례이다. No_grad()는 쉽게 말해, "다 비키고 신경꺼봐" 이다. 이 메소드는 pytorch의 DCG(Dynamic Computational Graph)에 영향을 주지 않고 regular python operation를 tensor에서 작동하게 한다. 또한, context manager로서의 역할도 한다고 한다. 모델이 validation 하는 동안 gradient를 계산하지 않도록 하는 효과가 있다(-> 나중에 또 나올 것이다)

tensor([1.0235], device='cuda:0', requires_grad=True)
  tensor([1.9690], device='cuda:0', requires_grad=True)

# Use pytorch no_grad()
with torch.no_grad():
  b -= lr * b.grad
  w -= lr * w.grad
 

b.grad.zero_()
w.grad.zero_()

>> tensor([1.0235], requires_grad=True)
>> tensor([1.9690], requires_grad=True)

결과가 잘 나온다!

Dynamic Computation Graph

"No gradient, No graph"

PyTorchViz 패키지를 사용하면 DCG를 쉽게 시각화할 수 있다. 이를 통해 앞에서 본 simple NN코드를 시각화 해보면, 다음과 같다.

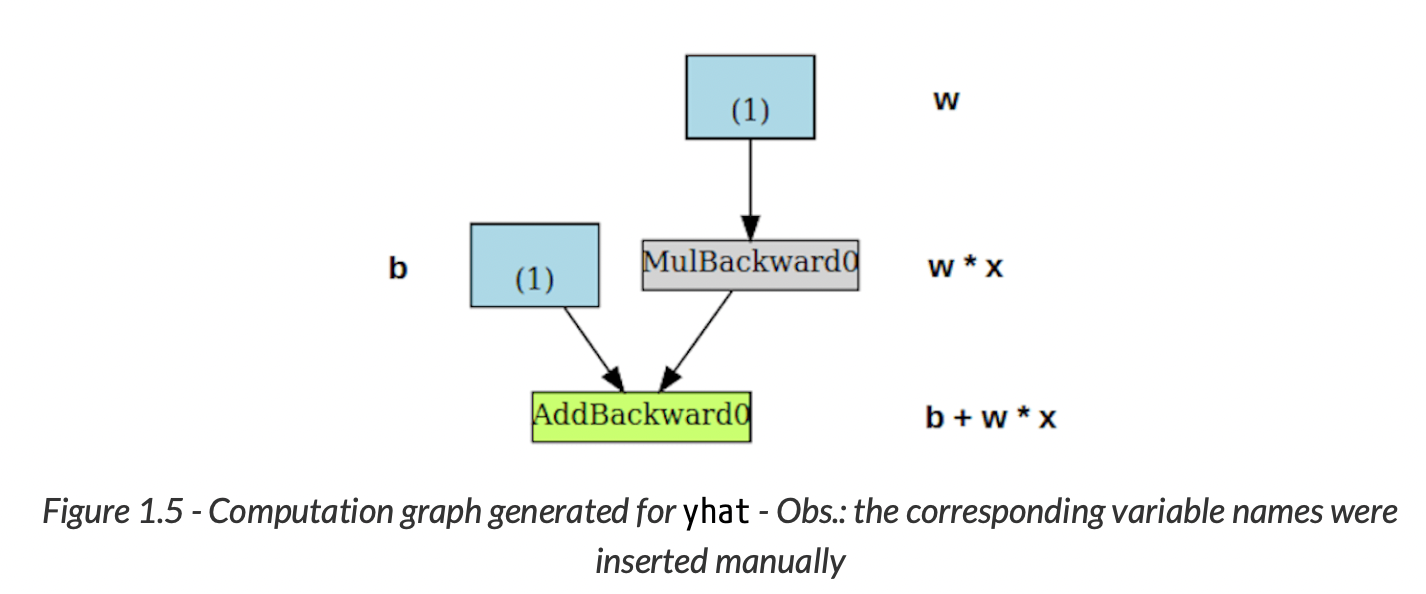
파란색 박스 (1) : 가중치로 쓰는 텐서들 <- 우리가 pytorch에게 gradient 계산해달라고 하는 바로 그 아이들

회색 박스(MulBackward0) : gradient를 계산하는 텐서, 혹은 그와 관련있는 텐서들을 포함하는 python operation

연두색 박스(AddBackward0) : 회색박스와 같지만, gradient 계산의 시작점이 다르다. Backward() 메소드를 loss 객체에서 call한 것을 떠올려보면, bottom-up 방식으로 계산되는 것을 알 수 있다.

초록색 박스를 자세히 보면, 두개의 화살표가 가르키고 있다. 두개의 변수 b와 w*x가 더해져서 이 초록색 박스의 operation이 되기 때문. 그리고 이 파란색 박스는 가중치 w로 부터 시작되었다.

회색 박스를 보면, multiplication 연산을 수행하고 있는 것을 알 수 있다(w*x). 그러나 오로지 하나의 화살표만 이 회색 박스를 가르키고 있다. 그리고 이 회색박스 또한 가중치 w로 부터 시작되었다.

---

딥러닝 관련해서 많은 책을 사고, 또 읽어봤지만 이 책 진짜 좋다. 파이토치 관련해서는 국내에 좋은 책을 찾아볼 수 없었는데, 내용이 많은 것을 제외하면 이해도 잘되고 자세하다! 찾아도 잘 안나왓던 가려운 부분을 눈높이에 맞게 잘 긁긁해준다!