부동 소수점 방식
컴퓨터에서 실수를 근삿값으로 표현할 때 사용합니다.
부동 소수점은 영어로 floating point로 둥둥떠다니는 소수점입니다.
- Floating Point Standard는 IEEE Std 754-1985에 정의되어 있다.
https://en.wikipedia.org/wiki/IEEE_754
부동 소수점 방식은 실수를 가수 부분과 지수 부분으로 나누어 표현하는 것을 말합니다.
이때 가수 부분은 유효 숫자를 나타내고 지수 부분은 소수점의 위치를 나타냅니다.
부동 소수점 방식은 고정 소수점 방식보다 넓은 범위의 수를 나타낼 수 있어서 과학 또는 수학 계산을 할 때 많이 이용됩니다.
하지만 근삿값으로 표현된다는 점과 고정 소수점 방식보다 연산 속도가 느리다는 점 때문에 부동 소수점 방식을 위한 별도의 연산 장치를 두는 경우가 많습니다.
부동소수점 또는 떠돌이 소수점 방식은 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수와 소수점의 위치를 풀이하는 지수로 나누어 표현한다
출처 : 위키백과
| 상대적 비교 | 부동 소수점 방식 | 고정 소수점 방식 |
|---|---|---|
| 연산 속도 | 느림 | 빠름 |
| 범위의 수 | 넓음 | 좁음 |
| 주 이용 | 과학, 수학 계산 | 보편적 |
| 표현값 | 근삿값 | 고정값 |
바이어스 표현법
8bit 바이어스 표현법으로 바꾸려면
127((2^8)-1)을 더해라 (127 = 0111 1111)
127(0111 1111)은 바이어스 표현법의 상수값
ex) 127(임의의 정수) + 바이어스 상수값 = 바이어스 표현법
0111 1111 + 0111 1111 = 1111 1110 바이어스 표현법
float 부동 소수점에서
지수부 = 바이어스 표현법
ex) -0.4 -> 32bit 부동 소수점으로 바꾸면.
먼저, 소수점을 2진수로 바꾸기 위해서는 2를 곱해서 나오는 1의 자리를 계산한다.
0.4*2 = 0.8 (1의 자리 0)
0.8*2 = 1.6 (1의 자리 1)
0.6*2 = 1.2
0.2*2 = 0.4
0.4*2 = 0.8
0.8*2 = 1.6
0.6*2 = 1.2
0.2*2 = 0.4
0.4*2 = 0.8
.
.
.
0110 0110 0110 ...
0.4 = 0.01100110... (2)
0.4 = 1.10011 * 2^-2
2^-2
-2 = 0000 0010
1111 1101
1111 1110
1111 1110 + 0111 1111 = 1111 1101따라서, 1 1111 1101 100 1100 1100 1100 1100 1100 이 된다.
byte / bit
1 byte = 8 bit
4 byte = 32 bit
int = 4 byte
char = 1 byte
float = 4 byte
정수 표현
출처 : https://www3.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html
Unsigned Integers
부호 없는 정수는 0과 양의 정수를 나타낼 수 있지만 음의 정수는 나타낼 수 없습니다. 부호 없는 정수의 값은 "기본 이진 패턴의 크기"로 해석됩니다.
| n | Minimum | Maximum |
|---|---|---|
| 8 | 0 | (2^8)-1 (=255) |
| 16 | 0 | (2^16)-1 (=65,535) |
| 32 | 0 | (2^32)-1 (=4,294,967,295) (9+ digits) |
| 64 | 0 | (2^64)-1 (=18,446,744,073,709,551,615) (19+ digits) |
Signed Integers
부호 있는 정수는 0, 양의 정수 및 음의 정수를 나타낼 수 있습니다. 부호 있는 정수에 대해 세 가지 표현 체계를 사용할 수 있습니다.
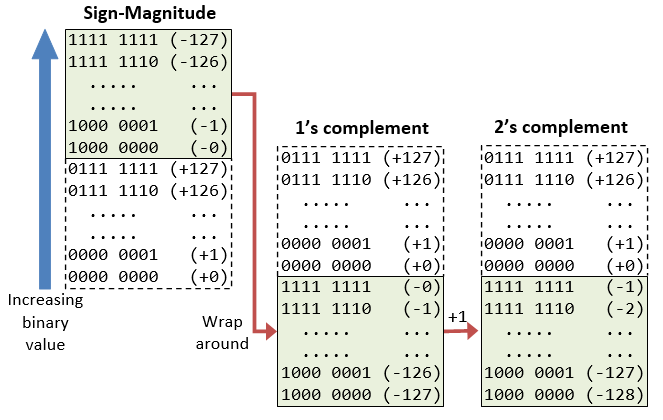
- Sign-Magnitude representation
- 1's Complement representation
- 2's Complement representation
위의 세 가지 방식 모두에서 최상위 비트(msb)를 부호 비트라고 합니다. 부호 비트는 정수의 부호를 나타내는 데 사용됩니다. 양의 정수는 0이고 음의 정수는 1입니다. 그러나 정수의 크기는 다른 체계에서 다르게 해석됩니다.
- n-bit Sign Integers in Sign-Magnitude Representation
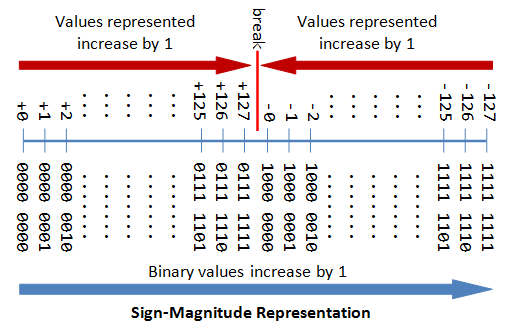
- n-bit Sign Integers in 1's Complement Representation
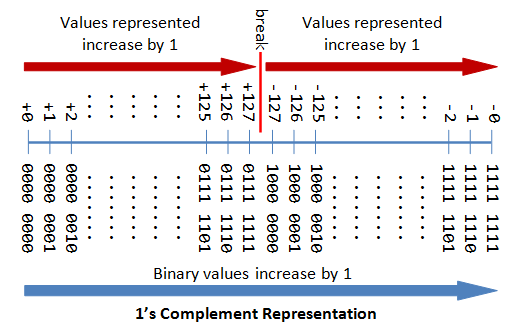
n-bit Sign Integers in 2's Complement Representation
| 정수 | 8bit |
|---|---|
| 127 | 0111 1111 |
| ... | ... |
| 3 | 0000 0011 |
| 2 | 0000 0010 |
| 1 | 0000 0001 |
| 0 | 0000 0000 |
| -1 | 1111 1111 |
| -2 | 1111 1110 |
| -3 | 1111 1101 |
| ... | ... |
| -127 | 1000 0001 |
| -128 | 1000 0000 |
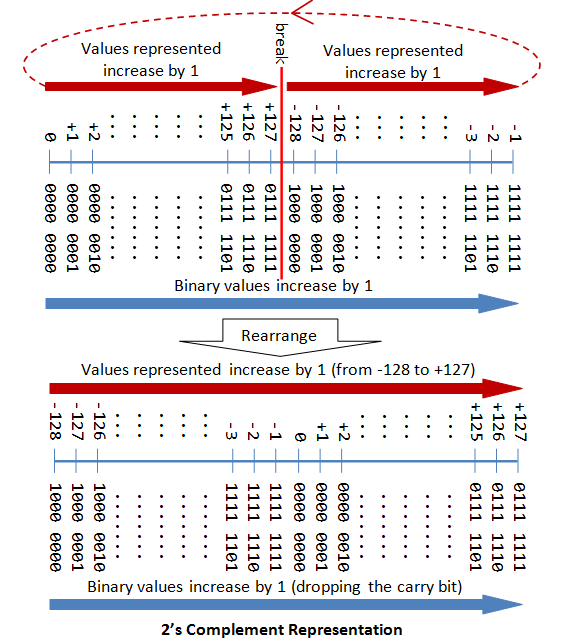
컴퓨터는 부호 있는 정수에 대해 2의 보수 표현을 사용합니다.
n비트 2의 보수 부호 있는 정수 범위
| n | minimum | maximum |
|---|---|---|
| 8 | -(2^7) | (=-128) |
| 16 | -(2^15) | (=-32,768) |
| 32 | -(2^31) | (=-2,147,483,648) |
| 64 | -(2^63) | (=-9,223,372,036,854,775,808) |
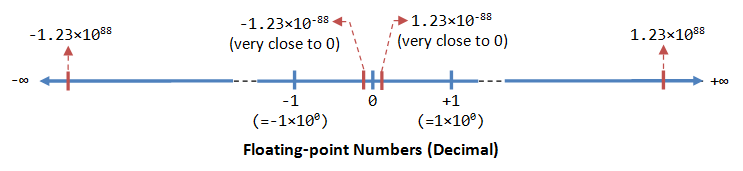
Floating-Point Number Representation
부동 소수점 수(또는 실수)는 매우 큰 값(1.23×10^88) 또는 매우 작은(1.23×10^-88) 값을 나타낼 수 있습니다.
또한 다음과 같이 매우 큰 음수(-1.23×10^88)와 매우 작은 음수(-1.23×10^88) 및 0을 나타낼 수 있습니다.
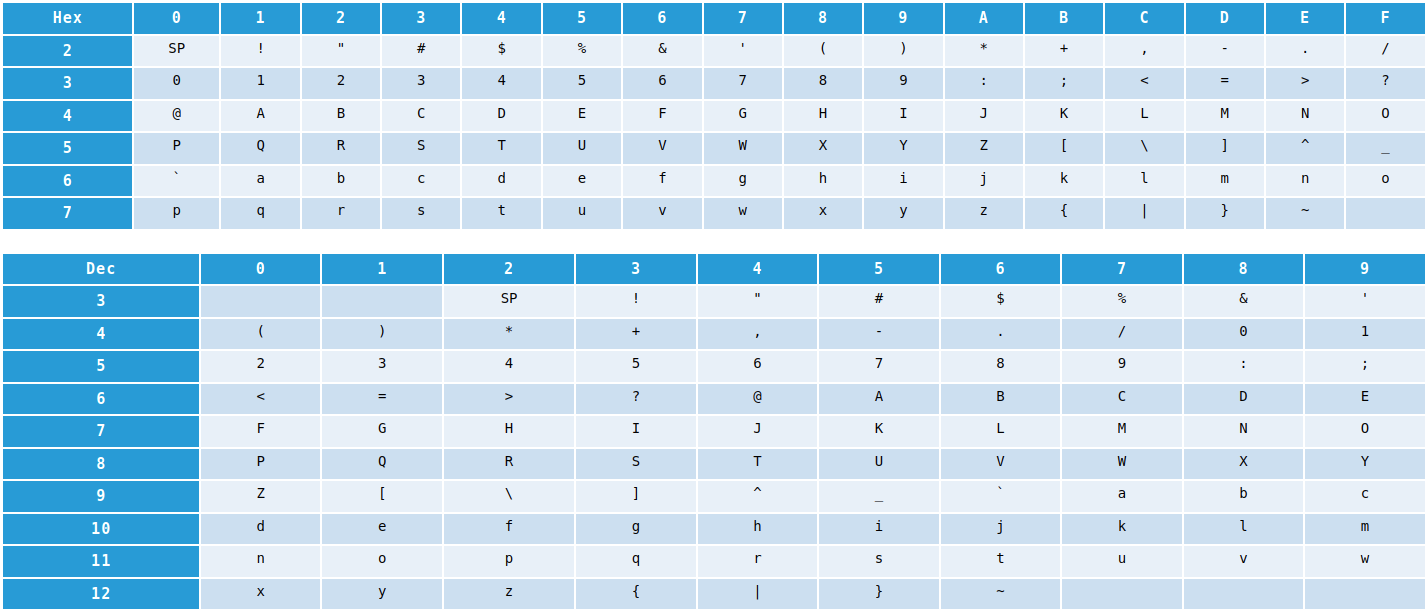
7-bit ASCII Code
(aka US-ASCII, ISO/IEC 646, ITU-T T.50)
ASCII(American Standard Code for Information Interchange)는 초기 문자 코딩 체계 중 하나입니다.
ASCII는 원래 7비트 코드입니다.
8비트 컴퓨터 메모리 구성을 더 잘 활용하기 위해 8비트로 확장되었습니다. (8비트는 원래 초기 컴퓨터에서 패리티 검사에 사용되었습니다.)
코드 번호 32D(20H) ~ 126D(7EH)는 다음과 같이 표 형식(16진수 및 10진수로 정렬)으로 인쇄 가능한(표시 가능한) 문자입니다.