[Ocaml] 고차함수

❓ 고차함수란

• 다른 함수를 인자로 받거나 리턴하는 함수
• 높은 추상화 ( abstraction ) 수준에서 프로그램을 작성하게 함.
• 간결하고 재활용 가능한 코드를 작성하는데 있어서 필수

❓ 추상화 ( abstraction )

▶ 복잡한 개념에 이름을 붙여서 속 내용을 모른 채 사용할 수 있도록 함.

ex) 2³ + 3³ + 4³ 을 계산하는 프로그램

• 단순하게 2x2x2 + 3x3x3 + 4x4x4 계산하도록 작성 가능
• 추상화시켜 계산하도록 작성하는 것이 복잡해질수록 더 좋음.

  let cube n = n x n x n
  in cube 2 + cube 3 + cube 4

▶ 모든 프로그래밍 언어는 추상화 도구로 변수와 함수를 제공

• 변수 : 반복적으로 사용하는 값에 붙인 이름
• (일차) 함수 : 반복적으로 사용하는 연산에 붙인 이름

▶ 고차함수 : 반복되는 프로그래밍 패턴에 붙인 이름

---

- List 예제

• List.map

1. int_all : 리스트의 모든 원소를 1씩 증가하는 함수

   

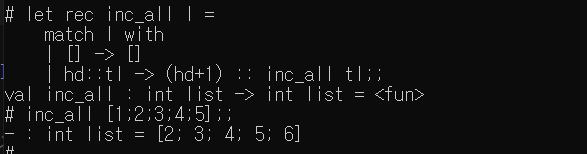
   • int_all : int list -> int list = < fun >

2. square_all : 리스트의 모든 원소를 제곱하는 함수

   

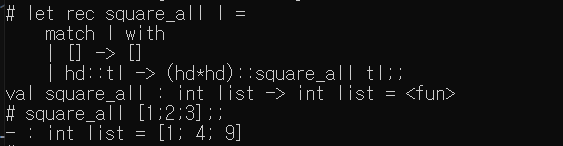
   • square_all : int list -> int list = < fun >

3. cube_all : 리스트의 모든 원소를 세제곱하는 함수

   

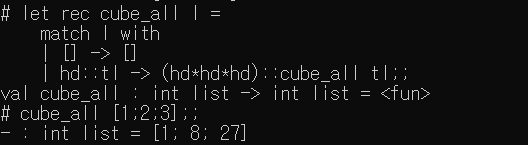
   • cube_all : int list -> int list = < fun >

• List.filter

1. even : 리스트의 모든 원소를 짝수인지 확인하는 함수

   

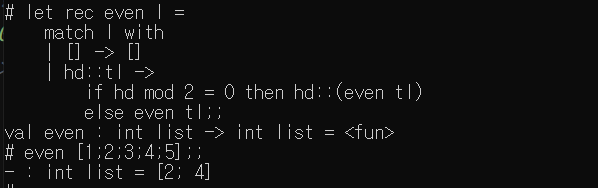
   • even : int list -> int list = < fun >

2. greater_than_five : 5보다 큰 원소만 출력

   

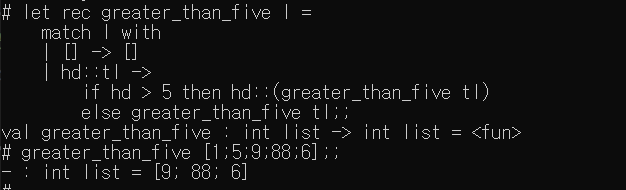
   • greater_than_five : int list -> int list = < fun >

• List.fold_right

1. sum : 리스트의 모든 원소를 합산한 값 출력

   

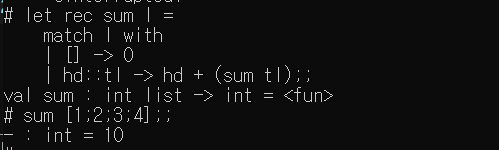
   • sum : int list -> int = < fun >

2. prod : 리스트의 모든 원소를 곱한 값 출력

   

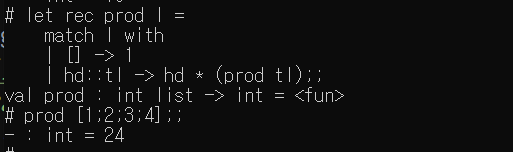
   • prod : int list -> int = < fun >

3. 1번과 2번을 하나의 고차함수로 나타냄

   1. fold_right : 직관적임.
      

      • fold_right : ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b = < fun >

   2. fold_left : tail-recursion 이므로 효율적임.
      

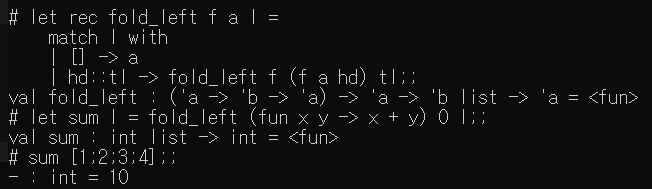
      • fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a = < fun >

• ❗ fold_right 와 fold_left의 차이점

  • 순서

    • fold_right는 리스트를 오른쪽에서 왼쪽으로

      fold_right f [ x; y; z ] init = f x ( f y ( f z init ) )

    • fold_left는 리스트를 왼쪽에서 오른쪽으로

      fold_left f init [ x; y; z ] f ( f ( f init x ) y ) z

  ▶ 결합법칙이 성립하지 않는 f에 대해서 결과가 다를 수 있음.
  ( ex : 10 - 3 != 3 - 10 )
  이와같은 상황에서는 fold_left 로 만들면 됨.

  • 타입
    • fold_right : ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b = < fun >
    • fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a = < fun >

  • fold_left 는 끝재귀호출 ( tail-recursion )

  ---

  ❗ fold_right 와 fold_left 의 차이점 비교 ( sub 연산 )
  ( 초깃값은 0이고, 10, 5, 2, 1 을 빼는 연산 )

  • fold_right 일 때 ( 결과 : 6 )
    ▶ 10 - ( 5 - ( 2 - ( 1 - 0 ) ) ) 의 순서로 연산

  • fold_left 일 때 ( 결과 : -18 )
    ▶ ( ( ( 0 - 10 ) - 5 ) - 2 ) - 1 의 순서로 연산

---

❗ roop 에 대응되는 개념이 fold 임.