[프로그래머스] 유한소수 판별하기

📚 문제 설명

소수점 아래 숫자가 계속되지 않고 유한개인 소수를 유한소수라고 합니다. 분수를 소수로 고칠 때 유한소수로 나타낼 수 있는 분수인지 판별하려고 합니다. 유한소수가 되기 위한 분수의 조건은 다음과 같습니다.

기약분수로 나타내었을 때, 분모의 소인수가 2와 5만 존재해야 합니다.

두 정수 a와 b가 매개변수로 주어질 때, a/b가 유한소수이면 1을, 무한소수라면 2를 return하도록 solution 함수를 완성해주세요.

🔎 제한사항

• a, b는 정수
• 0 < a ≤ 1,000
• 0 < b ≤ 1,000

🔎 입출력 예

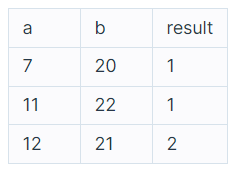
💻 코드

class Solution {
    public int solution(int a, int b) {

        int B = b / GCD(a,b);
        while (B != 1) {
            if (B % 2 == 0){
                B = B / 2;
            } else if (B % 5 == 0) {
                B = B / 5;
            } else {
                return 2;
            }
        }
        return 1;
    }
    
    // 유클리드 호제법! 두 수의 최대 공약수 구하기
    private int GCD(int a, int b) {
        if (b == 0) {
            return a;
        } else {
            return GCD(b, a % b);
        }
    }
}

📖 Solution

먼저 기약분수로 만들기 위해서는 두 수의 최대 공약수를 구해야한다.

최대 공약수를 구하기 위해서는 유클리드 호제법을 사용하면 된다!

유클리드 호제법

임의의 두 자연수 a, b가 주어졌을때, a를 b로 나눈 나머지를 n 이라고 하면 (a%b = n)
n이 0일때, b는 최대 공약수(GCD)다.

만약 n이 0이 아니라면, a에 b값을 다시 넣고 n를 b에 대입 한 후 다시 위 부터 반복하면 된다.

💡 재귀 함수를 이용한 유클리드 호제법

int GCD(int a, int b) {
    if (b == 0) {
        return a;
    } else {
        return GCD(b, a % b);
    }
}

💡 반복문을 이용한 유클리드 호제법

int GCD(int a, int b)
{
    int c;
    
    while(b) {
        c = a % b;
        a = b;
        b = c;
    }
    return a;
}