📚 문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한사항
- n은 2이상 1000000이하의 자연수입니다.
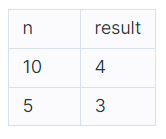
🔎 입출력 예
📖 Solution
🤔 처음으로 푼 방법 : 이중 for 문
가장 기본적인 이중for문을 사용해서 풀었다. 2부터 n까지 수를 다시 2부터 자기자신으로 나눠서 자기 자신으로만 나눠지면 소수라고 판단해 소수의 개수를 구하였다. 하지만 굉장히 효율적이지 못했고 결국 테스트 10 11 12 통과 못했다...
😮 두번째로 푼 방법 : 제곱근

프로그래머스 질문목록에 올려주신 글을 참고해서 2번째 방법으로 풀었다.
어떤 자연수 n이 있을 때, √n 보다 작은 모든 소수들로 나누어 떨어지지 않으면 n은 소수입니다.
먼저 101이 소수인지 아닌지 판별하기 위해서 우리는 √101을 구하면 10.xxx이 됩니다. 10보다 작은 소수는 일단 2, 3, 5, 7이 있습니다. 그런데 딱 봐도 이 4개의 소수로만 101이 나누어 떨어지지 않습니다. 그러므로 101소수입니다. 위의 방식을 이용하면 25개의 소수를 모두 이용해야 하지만 지금은 4개만 이용해도 쉽게 계산이 됩니다.
💻 수정 코드
import java.math.*;
class Solution {
public int solution(int n) {
int answer = 0;
boolean flag = true;
for(int i=2; i<=n; i++) {
for(int j=2; j<=Math.sqrt(i); j++) {
if(i%j==0) {
flag = false;
break;
}
}
if(flag==true) answer++;
flag = true;
}
return answer;
}
}코드를 보면 Math.sqrt()를 이용하여 제곱근 까지만 나눠보며 소수를 찾는것을 볼 수 있다. 하지만 효율성이 많이 떨어졌다..... 그래서 더 좋은 방법이 있을까 찾아보다가 마지막 방법을 찾을 수 있었다!
🧐 최종 방법 : 에라토스테네의 체 ⭐
수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.

🔎 알고리즘
-
2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
-
2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
-
자기 자신을 제외한 2의 배수를 모두 지운다.
-
남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
-
자기 자신을 제외한 3의 배수를 모두 지운다.
-
남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
-
자기 자신을 제외한 5의 배수를 모두 지운다.
-
남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
-
자기 자신을 제외한 7의 배수를 모두 지운다.
-
위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)
그림의 경우, 11^2 > 120이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.
💻 최종 코드
import java.math.*;
class Solution {
public int solution(int n) {
int answer = 0;
boolean[] number = new boolean[n+1];
// 소수가 아니면 true
for(int i=2; i <= Math.sqrt(n); i++) {
if(number[i] != true) {
for(int j=i*2; j<= n; j+=i) {
number[j] = true;
}
}
}
for(int i=2; i<=n; i++) {
if(number[i] == false) answer++;
}
return answer;
}
}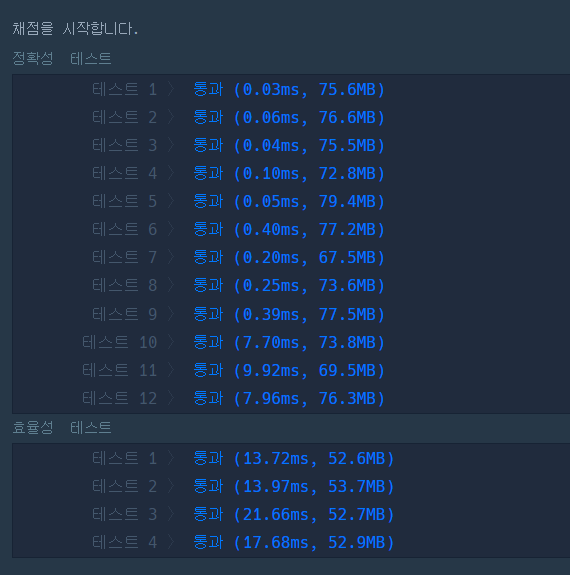
효율성이 전 방법보다 높아진걸 볼 수 있다! 🙌🏻

