다음 논문에 대한 포스팅입니다.
Szubert, Marcin, and Wojciech Jaśkowski. "Temporal difference learning of n-tuple networks for the game 2048." 2014 IEEE Conference on Computational Intelligence and Games. IEEE, 2014.

Introduction

2048 게임은 Gabriele Cirulli가 제작한 유명한 비디오 게임으로, 한 때 인터넷과 모바일에서 선풍적인 인기를 휩쓴 게임이다.

2048은 아래 그림과 같은 4x4 게임판에서 상하좌우 네 방향으로 타일을 슬라이드할 수 있으며, 같은 숫자의 타일을 합쳐 높은 숫자의 타일을 만들어내는 것을 목표로 한다.

2048은 easy-to-learn, hard-to-master의 속성을 가진 대표적인 게임으로, 인공지능 기술의 적용에 적합하다고 볼 수 있다.

2048의 기존 solver들은 트리 서치 기반이거나 휴리스틱으로, 본 논문에서는 Q-Learning, TD-state, 그리고 TD-afterstate라는 이름의 세 가지 학습 방법과 n-tuple network를 이용한 가치 함수 근사 방법을 통해 2048의 인공지능 solver를 고안했다.

Fig.1 예시

Game 2048

앞서 설명과 같이 2048은 Single-player, non-deterministic, perfect information video game이라고 한다. 4x4 보드의 각 타일은 빈 타일(empty tile) 혹은 v-tile로 구성될 수 있는데, 여기서 v는 2의 거듭제곱으로 $2^1\sim2^{17}$에 해당한다.

게임 시작 시 두 개의 빈 타일이 아닌 무작위 타일과 함께 시작한다.

무작위 타일은, 2-타일 혹은 4-타일이며, 빈 타일이 있던 위치 중 아무 곳에서나 무작위로 생성된다. (Fig.1-(a) 참조)

이후 상,하,좌,우 네 방향으로 타일들을 슬라이딩하여 같은 종류의 두 타일을 합쳐 새로운 (더 큰 숫자의) 타일을 만들 수 있다. (Fig.1-(b)~(d) 참조)

게임의 목표는 최대한 오래 게임을 지속시키면서 높은 점수를 얻는 것이다. 이와는 별개로 2048-타일을 만들어냈다면 그 게임은 이긴 것으로 간주한다.

Methods

A. Markov Decision Process

마르코프 의사결정 과정, 즉 MDP는 상태 S, 행동 A, 보상 R, 상태전이확률 P로 구성된 control 과정을 의미한다. 에이전트가 특정 상태에서 행동을 취했을 때 P의 확률로 다음 상태로 넘어가며, 이와 해당 다음 상태의 보상을 얻게 되는 프로세스이다.

본 환경에서 에이전트의 목적은 의사 결정(행동 선택)의 기준이 되는 정책 $\pi:S\rightarrow A$를 학습하는 것이다. 또 한가지 짚고 넘어가야 할 점은, 2048은 non-deterministic 환경으로, 이는 특정 행동을 취했을 때 무작위 타일이 생성되기 때문이다.

B. Temporal Difference Learning

TD는 매 time-step마다 value function을 업데이트하는 데 강점이 있는 강화학습의 큰 줄기 중 하나이다. 혹시 TD에 대해 잘 모르는 분은 검색을 통해 자세히 알아보고 오시기를 바람.

일반적인 TD(0)의 update rule은 다음과 같다.

$V(s)$란 상태 $s$에서의 상태 가치(state value), 장기적 보상(long-term reward) 혹은 효용성(utility)에 해당하는데, 행동에 따른 즉각적 보상 $r$과 대비된다.

위 수식에서 error에 해당하는 $\delta:=r+V(s'')-V(s)$를 TD error라고 부르며, 현재까지 계산된 $V(s)$와 현재 행동을 취해 얻어진 다음 상태 가치 $V(s'')$ 사이의 차이에 해당한다.

$\alpha\in[0,1]$는 학습률이다.

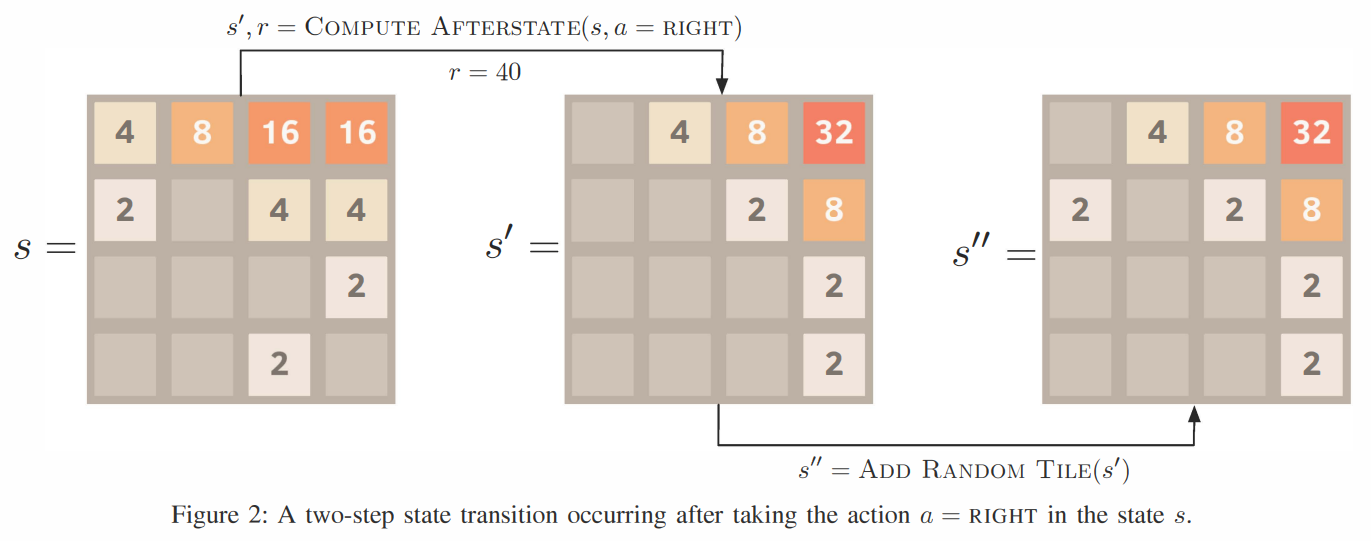
여기서 왜 $s'$가 아닌 $s''$로 표기되었는지 의아해할 수 있는데, 본 논문에서는 2048 게임의 특성을 고려하여 상태 전이 단계를 두 단계로 세분화했다. (Fig.2 참조)
1. 초기상태($s$)에서 타일 이동 후 상태 ($s'$,논문에서는 Afterstate라고 정의함)
2. Afterstate($s'$)에서 랜덤 타일이 추가된 다음 상태($s''$)

C. Learning Game-Playing Policies

먼저 전체적인 게임플레이 및 학습 과정을 살펴보자.

PlayGame
누적 보상 score와 초기상태 s를 초기화하고, Terminal state에 도달할 때 까지 iteration을 반복한다.
Evaluate 함수를 호출하여 특정 상태-행동 pair에 대한 가치 함수를 계산한 뒤 가장 높은 가치 함수를 갖는 행동 a를 선택, MakeMove함수를 호출해 다음 상태로 전이한다.
만약 학습과정이라면 LearnEvaluation 함수를 통해 학습을 진행한다.

이 때 가장 중요한 Evaluate 함수를 본 논문에서는 Introduction에서 언급했듯이 세 가지 방법으로 구현하고 있다.

1) Evaluating actions (Q-Learning)

action value function $Q(s,a)$를 이용한다. 이 방법에서 에이전트의 policy는 다음과 같다.

본 논문에서는 상태-행동 pair에 대한 $Q(s,a)$ 대신, 네 가지 행동(상/하/좌/우) 각각을 선택했을 때에 대한 $V_a(s)$를 정의해 사용한다.

Fig. 4 The action evaluation function and Q-Learning

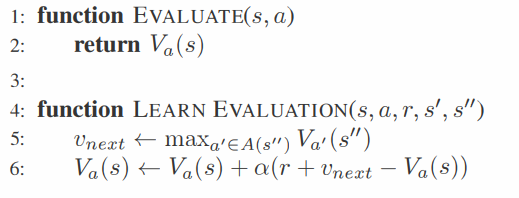
2) Evaluating states (TD-State)

상태 가치 계산을 위해서는 환경에 대한 정보, 즉 보상 R과 상태전이확률 P에 대해 알고 있어야 한다. 먼저 policy는 다음과 같다.

state evaluation function과 update rule은 다음과 같다.

Fig. 5 The state evaluation function and TD(0)

행동가치의 계산에 비해 상태가치 계산을 위해서는 가능한 모든 다음 상태에 대해 고려해야 한다. 2048의 경우 한번의 행동 이후 15 $\times$ 2 = 30가지의 서로 다른 상태로 전이할 수 있는데, 이는 afterstate에 최대 15개의 빈 타일이 만들어질 수 있고, 이 빈 타일에 두개의 서로 다른 랜덤 타일이 생성되기 때문이다.

따라서 1)의 경우보다 계산이 느리고 많은 메모리 용량을 차지한다는 단점이 있다.

3) Evaluating afterstates (TD-Afterstate)

한 행동에 의해 만들어지는 afterstate는 deterministic하게 하나만 존재하므로, TD-State보다 훨씬 빠르다. 이 경우 에이전트의 policy는 다음과 같다.

$T(s,a)$는 상태 $s$에서 행동 $a$를 취했을 때 이어지는 afterstate $s'$로의 mapping이다.

학습 과정을 살펴보면, 특정 상태에서 어떤 행동을 했을 때 계산되는 afterstate value값을 최대로 하는 행동 a_next를 선택하여 취한다. 그렇게 전이되어 나오는 afterstate s'_next와 r_next를 이용해 afterstate value V(s')를 업데이트하는 방식이다.

D. N-tuple Network Evaluation Function

작은 상태 공간의 경우, look-up table과 같은 형태로 모든 V값을 저장하고 바로 참조하여 사용할 수 있다. 그러나 2048의 경우 $(4\times4)^{18}\approx4.7\times10^{21}$개의 가능한 상태가 존재한다. (빈타일~$2^{17}$-타일, 보드 크기 4x4)

따라서 모든 상태에 대한 개별적인 V값을 저장해두는 것은 불가능하고, V값을 근사하기 위한 파라미터화된 함수 (신경망)이 필요한데, 그것이 바로 n-tuple network이다. n-tuple network는 이미 Othello, Connect 4와 같은 게임에서 좋은 성적을 거둔 바가 있다.

n-tuple network는 $m$개의 $n_i$-tuple들로 이루어져 있다. 여기서 n는 튜플의 크기가 되겠다. $i=1...m$에 대해 i번째 n-tuple은 look-up table $LUT_i$와 보드 위의 위치에 해당하는 $(loc_{ij})_{j=1...n_i}$로 구성된다. LUT는 각각의 보드 패턴 sequence 에 대한 가중치(weight) 파라미터를 저장하고 있다.

n-tuple network를 함수 $f$에 대한 수식으로 다음 그림과 같이 나타낼 수 있다.

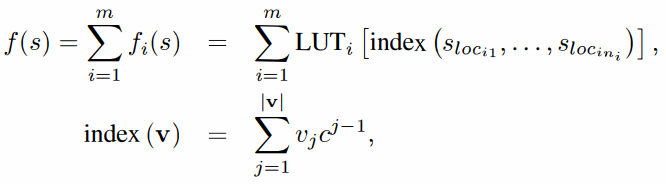
이 때 $s_{loc_{ij}}$는 보드 위의 한 위치인 $loc_{ij}$에서의 값(타일의 값)을 의미하는데, 타일 값은 빈 타일은 0, 값이 있는 $v$-타일은 $log_2v$로 나타낸다. (e.g. 128-타일은 7로 인코딩됨)

$\textbf v$는 타일 값들을 담고 있는 벡터로, 각각의 원소 $v_j$는 $0\le v_j<c \;(j=1...|\textbf v|)$인데, $c$는 가능한 타일값들의 개수를 나타낸다.
2048게임에서는 최대 $2^17$-타일이 가능하므로 c는 18에 해당하나, 본 논문에서는 weight 개수를 제한하기 위하여 c=15로 설정했다.

다음 그림과 함께 예시를 들어보겠다.

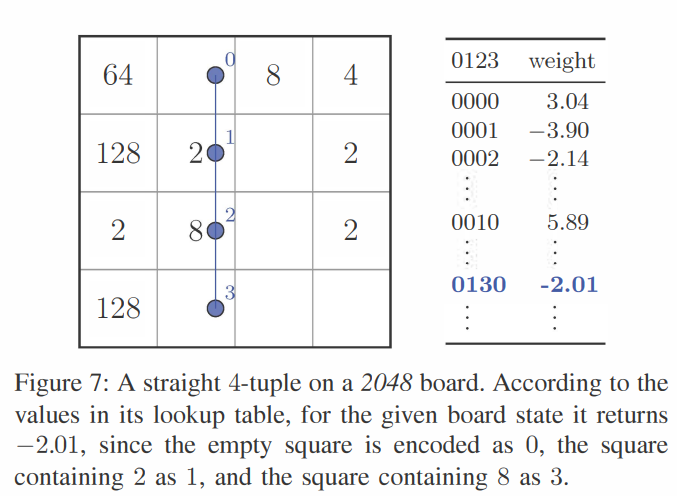
위 그림과 같은 보드 상황에서, 4-튜플의 weight값은 (단, m=1일 때)

의 과정으로 weight를 참조한다.

Comparison of the Learning Methods

Q-Learning, TD-State, TD-Afterstate 세 가지 방법 간의 성능 비교 실험

A. Experimental Setup

1) N-tuple network architecture
n-tuple network의 디자인에 있어서 고려해야 할 중요한 사항 중 하나는 게임 보드 위에서의 개별 n-tuple들의 위치라고 한다. 반드시 그래야 하는 것은 공간적인 특성을 반영하기 위해 연속적인 위치에 튜플을 올려놓는 것이 좋다고 한다.

2048에서는 한 개의 n-tuple은 $15^n$개의 weights를 지닌다. (c=15이기 때문에) 따라서 본 실험에서는 그나마 manageable한 숫자로서 n=4를 선택했다. 4개의 수평 튜플, 4개의 수직 튜플, 9개의 사각형모양 튜플로 총합 17개의 4-튜플로 network를 구성했다. (Fig. 8 참조) 따라서 weight의 수는 $17\times15^4=860,625$개이다.

2) Learning algorithms

1. Q-Learning : 상,하,좌,우 네 가지 행동에 대한 개별적인 n-tuple network를 사용해 value function($V_{up},V_{down},V_{left},V_{right})$을 근사한다. update rule은 물론 Fig.4의 Q-learning 방법을 따른다.
2. TD-State : 한 행동으로부터 만들어질 수 있는 모든 경우의 상태에 대해 V를 계산한다. 상태전이확률과 reward function에 대한 사전 정보를 필요로한다. Fig.5의 TD(0) update를 따라 학습한다.
3. TD-Afterstate : 한 행동으로부터 만들어지는 deterministic한 afterstate value를 계산한다. 마찬가지로 Fig.6의 update rule에 따르며, afterstate 계산을 위한 게임 모델을 필요로 한다.

위 세 가지 방법 모두 어떤 행동이 이루어진 후에 학습이 진행되며, n-tuple network($f$)를 이용해 value function을 근사한다.

3) Performance measures

• Winning rate $\in [0,1]$ : 1000번의 게임 플레이 중 2048-타일을 만들어낸 횟수(비율)
• Total score : 1000번의 게임 플레이 중 얻어낸 총 점수의 평균
• Learning time : 에이전트 학습에 소요된 시간

B. Results

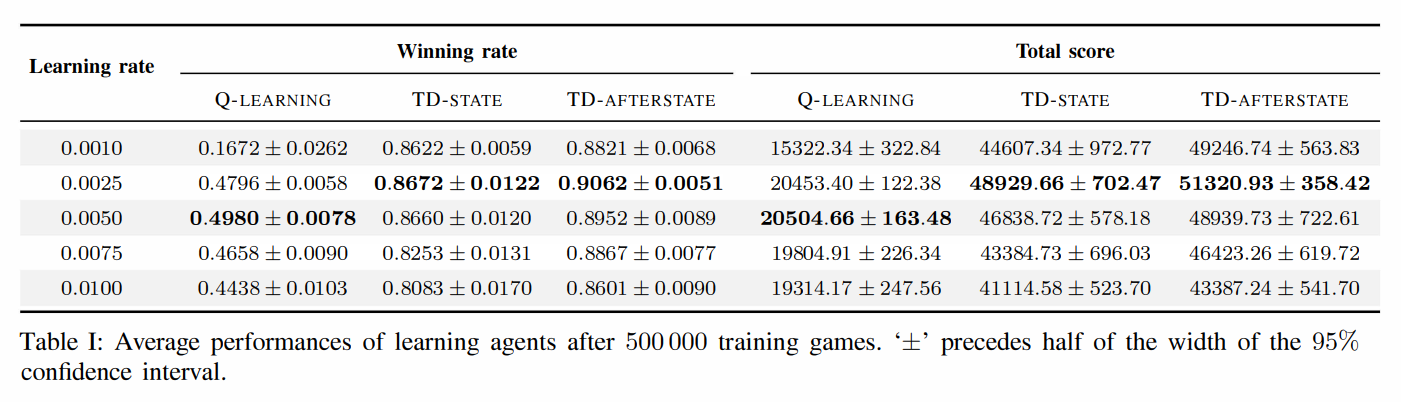
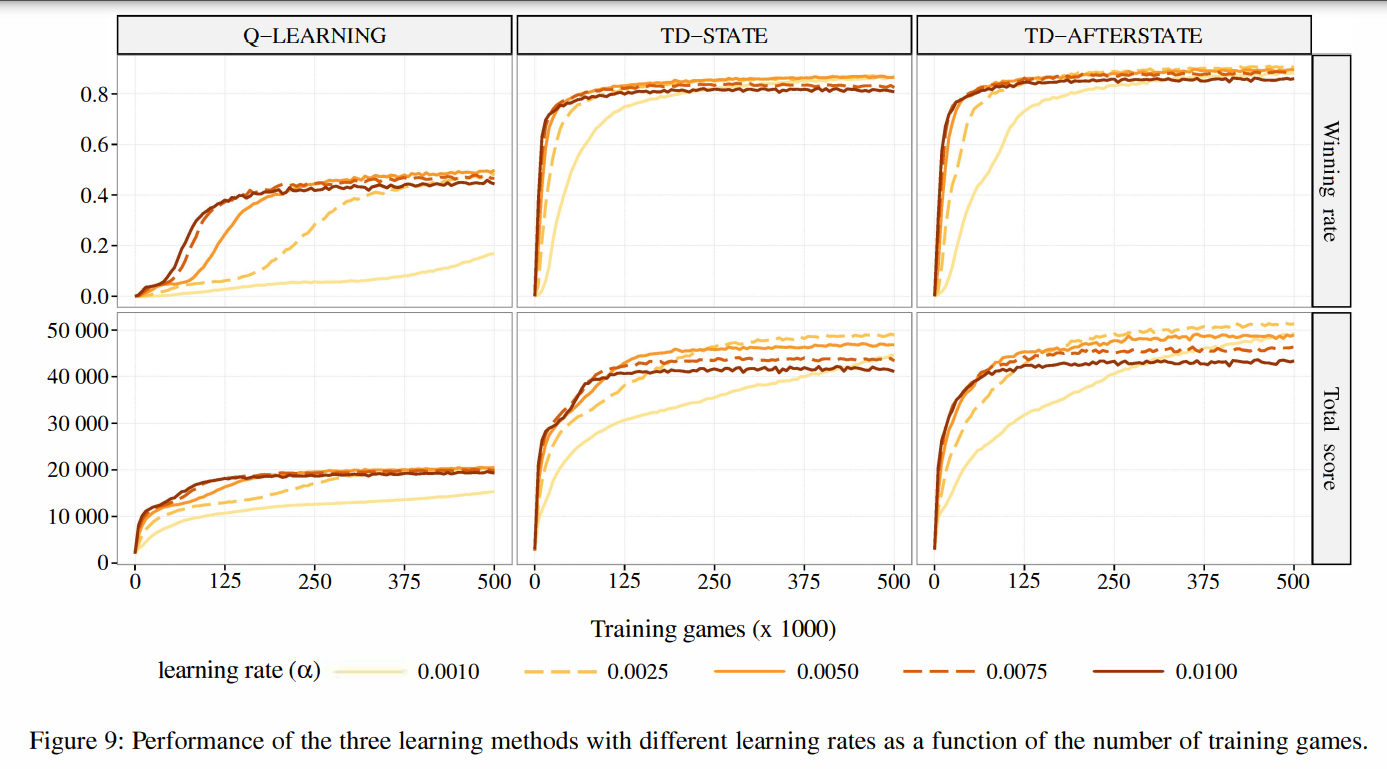
TD-State와 TD-Afterstate가 Q-Learning에 비해 훨씬 좋은 성적을 냈다. 둘 사이의 차이가 근소하긴 하지만, TD-Afterstate의 학습 속도가 현저히 빨랐다고 한다.

Improving the Winning Rate

간단하게만 소개하자면, computational resource를 좀더 늘리고 성능을 극대화한 실험이다.
이전 실험에서 가장 좋은 성적을 냈던 TD-Afterstate ($\alpha=0.025$)를 사용했고, 2개의 직선형 4-tuple, 2개의 직사각형 6-tuple을 사용하여 $2\times15^4+2\times15^6=22,882,500$개의 weights로 이전 실험에 비해 훨씬 많은 weight를 사용해 network를 구성했다.

또한 symmetric sampling 기법을 사용하여 게임 보드의 대칭성을 활용하여 성능을 높였다고 하는데, 보드의 rotation과 reflection을 통해 한 튜플당 8개의 값을 얻어낼 수 있다.
이게 무슨 말이냐면, 현재 보드에 회전, 반전 등의 Affine 변환을 가한 뒤 변환된 보드 위에 N Tuple Networks를 덧대어 Value값을 계산했다는 것이다. 더 적은 N Tuple들로 일종의 일반화 성능을 올리고자 하는 휴리스틱인 듯 하다.

실험 결과 winning rate 97.0%, total score 99,916 $\pm$ 1290를 기록했다고 한다.

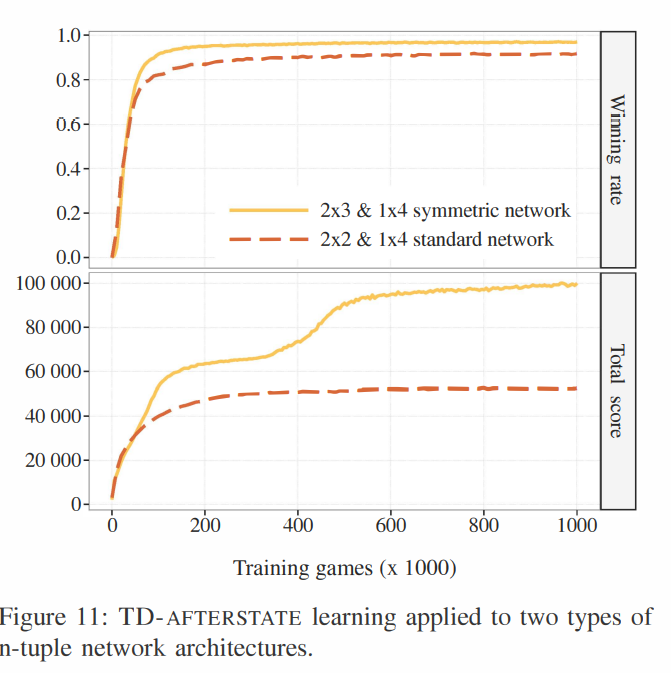
Fig. 11에는 본 실험의 학습 곡선이 나와 있는데, 약 350,000 games에서 total score가 정체되는 구간이 발생한다.
저자들의 설명에 의하면, 저 구간 전까지는 $2^{14}=16,384$-타일 미만의 타일만 만들어내다가, 저 구간부터 어찌어찌해서 16,384-타일 이상의 타일들을 생성하는 요령을 에이전트가 알아내어 평균 total score가 상승하게 된 것이라고 한다.

Discussion

A. Winning Rate vs. Total Score

따라서 Fig.11의 실험 결과를 살펴보면, winning rate는 거의 동일한 값을 유지하는데 total score만 높아지는 부분을 확인할 수 있다. 이는 에이전트가 winning rate, 즉 2048-타일의 생성이 아닌 최대한 높은 점수(total score)를 얻는 것을 목표로 학습을 진행했기 때문이라고 논문의 저자들은 보고 있다.

B. Comparison with Search-Based Agents

Introduction에서 언급했듯이, 2048의 기존 알고리즘들은 트리 서치 기반의 알고리즘이었다.

• 첫번째 방법은 Minimax game tree search + $\alpha-\beta$ pruning 방법으로, winning rate 89%로 본 연구에 비해 현저히 낮다.
• 두번째는 Minimax의 변종인 Expectimax (depth limit of 8 moves)로, winning rate 100%에 달하지만 이는 고작 100개의 게임에서 측정된 결과이므로 overestimated되었을 가능성이 높다. 속도를 비교하자면, C언어로 짜여진 효율적인 implementation에서도 평균 6.6 move/seconds의 실행 속도를 보여주는데, 이는 본 연구의 solver가 330,000moves/seconds를 보이는 것에 비하면 50,000배나 느린 속도라고 한다.

위 비교 결과는 학습기반 알고리즘과 탐색기반 알고리즘 간의 trade-off를 여실히 보여준다.
전자는 적은 computational power를 사용하지만 evaluation function을 저장하기 위한 많은 메모리를 필요로 하고, 후자는 적은 메모리를 사용하지만 연산량의 문제가 있다.

C. Lack of Exploration

마지막으로 본 논문의 저자들은 $\epsilon-greedy$와 같은 explicit한 exploration 방법을 채택하지 않았다는 점을 지적했는데, 이는 랜덤 타일이 생성되는 2048 게임 환경의 특성상 충분히 stochastic하고 diversified되었기 때문이라고 한다.