
Tree
- 비선형 자료 구조로 계층 모델이다.
- 그래프의 한 종류
- 사이클(Cycle)이 없는 하나의 연결 그래프
- DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프의 한 종류
- 노드가 N개인 트리는 항상 N-1개의 간선을 갖는다.
- 연결되지 않은 노드가 존재하지 않는다.
- 임의의 노드에서 다른 노드로 가는 경로(Path)는 유일하다.
Binary Tree
- 각 노드가 최대 2개의 자식을 갖는 트리
- 공 집합(empty)도 노드가 있는 것으로 간주한다.

그림을 보면 알 수 있듯 오른쪽 자식만 있어도 이진 트리이다.
Full Binary Tree
- 모든 노드가 0 혹은 2개의 자식 노드를 갖는 트리
또는 leaf 노드의 자식 노드가 0개인 트리


Complete Binary Tree
- 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 이진 트리
또는 마지막 level을 제외한 모든 level에서 노드들이 꽉 채워진 이진 트리

Perfect Binary Tree
- 모든 level에 모든 노드가 채워져 있는 트리 / 모든 leaf 노드의 level이 동일하다.
- 트리의 높이가 h일 경우, 노드의 개수는 N = 2^(h+1)-1
※ N = 2^(h+1)-1 공식 유도


Binary Search Tree (BST)
- 정렬된 이진 트리
- 이진 트리 + LinkedList의 장점을 결합
규칙
- 중복된 값을 허용 x
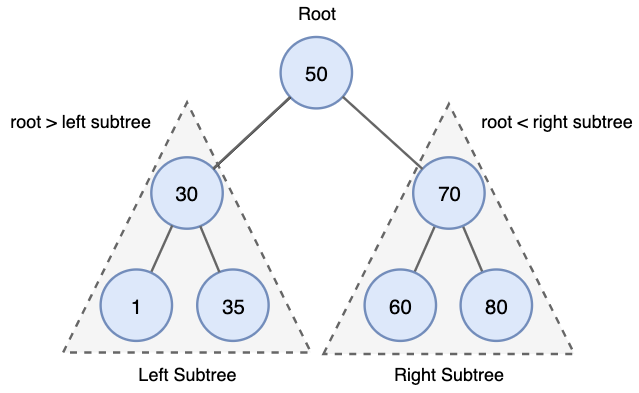
- 항상 부모의 값 > 왼쪽 자식 값
- 항상 부모의 값 < 오른쪽 자식 값
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
시간 복잡도
- 균형 상태의 경우: O(logN) / Skrewed Tree의 경우: O(n)
삽입
- 탐색을 실패한 위치가 바로 새로운 노드를 삽입하는 위치
탐색
- 찾으려는 원소값과 현재 노드의 값을 비교해 간다.
- 찾으려는 값 < 현재 노드 값: 왼쪽으로 이동
- 찾으려는 값 > 현재 노드 값: 우측으로 이동
삭제
- 세 가지 상황이 주어진다.
- 삭제하려는 노드의 자식 노드가 없는 경우
- 삭제하려는 노드의 자식이 한 개인 경우
- 삭제하려는 노드의 자식이 두 개인 경우
※ <이진 탐색트리> 탐색,삽입,삭제 알고리즘 및 시간 복잡도 분석
Red-Black Tree
- BST를 기반으로 하는 트리 자료 구조
- Search, Insert, Delete 에 O(logN)의 시간이 걸린다.
조건
- Root Property: 루트 노드의 색깔은
BLACK이다. - External Property: 모든 external 노드들은
BLACK이다. - Internal Property: 빨간 노드의 자식들은 모두
BLACK이다. - Depth Property: 모든 리프 노드에서 Black Depth는 같다.
- 리프 노드에서 루트 노드까지 가는 경로의
Black노드의 개수는 같다.
- 리프 노드에서 루트 노드까지 가는 경로의
삽입
- 삽입할 때, 삽입되는 노드의 색깔은
RED이다. - 삽입을 진행시, 3번 조건에 어긋난다. 이때,
RestructuringorRecoloring이 수행된다.

Restructuring
- 순서 결정 및 트리를 만드는 시간: O(1) + 현재 노드가 들어갈 위치를 찾는 시간: O(logN) = 총 시간 복잡도: O(logN)
Recoloring
- Propagation이 발생할 수 있다. (ex. 현재 노드의 색깔이
RED인데 그 부모 노드의 색깔도RED인 경우) - 양쪽 모두
BLACK이 1씩 증가하므로 4번 조건에 부합된다. - 현재 노드가 들어갈 위치를 찾는 시간: O(logN) + Root까지 Propagation: O(logN) = 총 시간 복잡도: O(logN)
최악의 경우 Restructuring, Recoloring 둘 다 O(logN)의 시간이 걸린다.
※ 과정은 알고리즘 ) Red-Black Tree 에서 확인 가능하다.
