백트래킹이란?
모든 경우의 수를 전부 고려하는 알고리즘 상태공간을 트리로 나타낼 수 있을 때 적합한 방식이다. 일종의 트리 탐색 알고리즘이다. 방식에 따라 DFS, BFS BFS가 있다.
다시 말해, DFS를 사용하여 경로를 탐색하되, 주어진 조건에 일치하지 않는 경우 다시 이전 단계로 돌아가 다른 경로로 탐색을 하는 것이다.
필자는 처음 백트래킹 정의를 보고 DFS를 통해 모든 경로를 탐색하는 것하고 무엇이 다른 지 알지 못하여, 이해하는데 시간이 오래 걸렸다.
이후 생각해보니, 모든 경로를 탐색하는 개념은 동일하지만, 백트래킹은 경로 탐색 중 조건에 부합하지 않거나 or 해가 아닌 경로일 경우 굳이 더 탐색하지 않고 이전 노드로 돌아와 다른 경로를 탐색하는 방식이였다.
즉, DFS를 통한 모든 경로 탐색에 조건을 추가했을 뿐이다.
예시
예를 들어, 다음과 같은 트리가 있다고 가정하자.
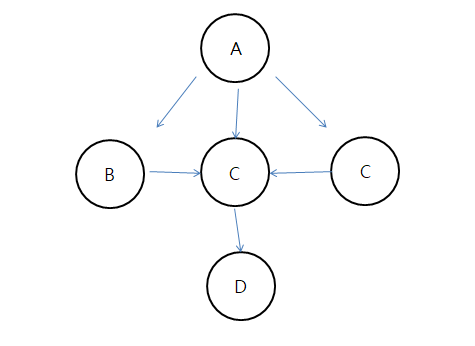
일반적인 DFS일 경우, A에서 출발한다고 가정하면, 생성되는 경로는 다음과 같다.
- ABCD
- ACD
- ACCD
하지만, 여기에 동일한 알파벳은 경로에 포함되지 않는다는 조건이 추가될 경우 생성되는 경로는 다음과 같다.
- ABCD
- ACD
- AC
백트래킹에서의 움직임을 살펴보면,
1. A -> C(오른쪽)
2. C(오른쪽)에서 C(가운데)로 이동할 수 없기 때문에 A로 돌아간다. (이 부분을 백트래킹이라고 말한다.)
3. A -> C -> D
즉, 백트래킹은 그저 조건에 부합하지 않을 때 다시 이전에 거쳐온 노드로 돌아가 다른 경로를 탐색하는 것이다. DFS하고 유사하기 때문에 겁낼 필요 없다.
백준 1987 : 알파벳
문제 링크 : https://www.acmicpc.net/problem/1987
세로 R칸, 가로 C칸으로 된 표 모양의 보드가 있다. 보드의 각 칸에는 대문자 알파벳이 하나씩 적혀 있고, 좌측 상단 칸 (1행 1열) 에는 말이 놓여 있다.
말은 상하좌우로 인접한 네 칸 중의 한 칸으로 이동할 수 있는데, 새로 이동한 칸에 적혀 있는 알파벳은 지금까지 지나온 모든 칸에 적혀 있는 알파벳과는 달라야 한다.
즉, 같은 알파벳이 적힌 칸을 두 번 지날 수 없다.
좌측 상단에서 시작해서, 말이 최대한 몇 칸을 지날 수 있는지를 구하는 프로그램을 작성하시오. 말이 지나는 칸은 좌측 상단의 칸도 포함된다.
초기 접근
- 스택을 이용한 DFS를 사용하자
- 현재 경로에 추가된 알파벳을 배열에 집어넣어 python의
in키워드를 통해 중복 여부를 검사하자 - 어느 노드에 방문할 때마다 인접한 노드들을 스택에 집어넣자. DFS는 이렇게 구현하는 것 아닌가?(DFS를 잘못 이해했었다.)
해결한 접근
위 접근들에서 문제가 되는 부분들은 무엇일까? 사실 전부 잘못된 접근이였다. 먼저, 스택을 이용하여 DFS를 구현하는 것은 맞다. 하지만, 이 문제의 핵심은 조건에 일치하는 모든 경로를 탐색하는 것이다.
특정 노드의 인접 노드들이 조건에 부합할 지라도, 추후 다른 노드들이 추가되면서 이전에 추가한 노드들은 더이상 조건을 충족시키지 못할 수도 있다. 따라서, 인접한 노드들을 추가하지말고, 방문했던 노드들만 스택에 추가하여야 한다.
그런데, 이렇게 하면 추가적인 문제가 있다. 이전에 방문했던 노드들로 돌아갔을 때, 해당 노드에서 방문하지 않은 노드들을 탐색해야 하기 위해 이를 기억해 두어야 한다. (만약, 재귀함수를 사용하면 따로 데이터를 저장하지 않아도 된다. 콜스택에서 함수의 실행 과정을 저장해 두기 때문이다.)
필자는 이부분을 해결하기 위해 스택에 추가될 노드의 구조를 다음과 같이 설정하였다.
[행 번호, 열 번호, 인접 노드 확인을 위한 반복문의 시작 번호]
이제 남은 문제는 2번이다. in 키워드는 생각보다 시간복잡도가 크다. list에서는 모든 요소를 순회하기 때문에 O(n)의 복잡도를 갖고, set에서는 O(1) ~ O(n)의 복잡도를 갖는다. 이 부분을 언급하는 이유는 in키워드를 사용하여 백준 체점에서 시간초과가 발생했기 때문이다.
이 부분을 해결하기 위해 길이가 26인 boolean배열을 사용하였다. 알파벳은 26개이기 때문에, 알파벳이 경로에 추가될 경우 해당하는 배열 요소를 True로 바꿔놓았다. 만약 경로에서 알파벳이 제거되면 False로 변경하였다.
스택을 이용한 코드
R, C = map(int,input().split(" "))
graph = []
for _ in range(R):
graph.append(list(input()))
visited = [False for _ in range(26)]
ans = 0
stack = []
stack.append([0,0,0])
def is_visited(r,c):
alphabet = graph[r][c]
alpha_num = alpha_to_num(alphabet)
return visited[alpha_num]
def alpha_to_num(alphabet):
return ord(alphabet) - 65
dx = [0,0,-1,1]
dy = [-1,1,0,0]
while stack:
cur_r, cur_c, i = stack[-1]
if not is_visited(cur_r,cur_c):
visited[alpha_to_num(graph[cur_r][cur_c])] = True
if len(stack) > ans:
ans = len(stack)
end = True
for j in range(i,4):
nx = cur_r + dx[j]
ny = cur_c + dy[j]
if 0 <= nx < R and 0 <= ny < C and not is_visited(nx,ny):
stack[-1][2] = j + 1
stack.append([nx,ny,0])
end = False
break
if end:
x, y, temp = stack.pop()
last_item = graph[x][y]
visited[alpha_to_num(graph[x][y])] = False
print(ans) 재귀함수를 이용한 코드
r,c = map(int,input().split())
maps = []
for _ in range(r):
maps.append(list(input()))
ans = 0
alphas = [False for _ in range(26)]
dx = [-1,1,0,0]
dy = [0,0,-1,1]
def is_visited(r,c):
alphabet = maps[r][c]
alpha_num = alpha_to_num(alphabet)
return alphas[alpha_num]
def alpha_to_num(alphabet):
return ord(alphabet) - 65
def dfs(x, y, count):
global ans
ans = max(ans, count)
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < r and 0 <= ny < c and not is_visited(nx,ny):
alphas[alpha_to_num(maps[nx][ny])] = True
dfs(nx, ny, count+1)
alphas[alpha_to_num(maps[nx][ny])] = False
alphas[alpha_to_num(maps[0][0])] = True
dfs(0,0,1)
print(ans)결론
재귀함수의 코드가 훨씬 깔끔한 것을 볼 수 있다. 그 이유는 재귀함수에서는 콜스택에 함수 실행 과정이 저장되기 때문이다. 스택에서는 따로 변수를 생성하여 노드에서 경로를 탐색할 차례를 저장해두어야 한다.
백트래킹과 같이 이전의 경로로 돌아가서 다시 탐색하는 경우, 함수의 실행 과정을 저장해두기 위해 재귀함수로 구현하는 방식이 더 적절한 것 같다.

