참고자료
유전 알고리즘이란?
유전 알고리즘(Genetic Algorithm)은 1975년 존 홀랜드에 개발된 전역 최적화 기법(시간이 걸리더라도 전체 탐색영역에서 가장 좋은 해를 찾는 것)으로, 최적화 문제를 해결하는 기법의 하나이다. 자연 세계의 진화 과정에 기초한 계산 모델로서 생물의 진화를 모방한 진화 연산의 대표적인 기법이다. 실제 진화의 과정에서 많은 부분을 차용하였으며, 변이, 교배 연산 등이 존재한다.
유전 알고리즘은 어떤 미지의 함수 Y = f(x)를 최적화하는 해 x를 찾기 위해, 진화를 모방한(Simulated evolution) 탐색 알고리즘이라고 말할 수 있다. 유전 알고리즘은 특정한 문제를 풀기 위한 알고리즘이라고 보다는 문제를 풀기 위한 접근방법에 가까우며, 유전 알고리즘에서 사용할 수 있는 형식으로 바꾸어 표현할 수 있는 모든 문제에 대해 적용할 수 있다.
구성
개념
- 염색체(chromosome) : 생물학적으로는 유전 물질을 담고 있는 하나의 집합을 의미하며, 유전 알고리즘에는 하나의 해(solution)를 표현한다. 어떠한 문제의 해를 염색체로 인코딩(encoding)한다.
- 유전자(gene) : 염색체를 구성하는 요소로써, 하나의 유전 정보를 나타낸다. 어떠한 염색체가 [A B C]라면, 이 염색체에는 각각 A, B 그리고 C의 값을 갖는 3개의 gene이 존재한다.
- 자손(offspring) : 특정 시간 t에 존재했던 염색체들로부터 생성된 염색체를 t에 존재했던 염색체들의 자손이라고 한다. 자손은 이전 세대와 비슷한 유전 정보를 갖는다.
- 적합도(fitness) : 어떠한 염색체가 갖고 있는 고유값으로써, 해당 문제에 대해 염색체가 표현하는 해가 얼마나 적합한지를 나타낸다.
- 교차율 또는 교배(crossover) : 2개의 염색체를 조합하여 새로운 염색체를 생성한다. 보통 교차율은 0.7(70%)로 정의한다.
- 돌연변이(mutation) : 생물학적 돌연변이와 같은 것으로 특정 확률로 염색체 또는 유전자를 변형한다. 변이 없이 알고리즘을 진행하다보면 여러 세대가 지나고 같은 데이터를 가진 염색체만 남는 경우가 있다. 변이를 통해 새로운 데이터에 대해 가능성을 열어둔다. 보통 변이율은 0.001(0.1%)로 정의한다.
유전 알고리즘을 활용하기 위한 요구 조건
- 해를 유전자(gene)의 형식으로 표현할 수 있어야 한다.
- 해가 얼마나 적합한지를 적합도 함수를 통해 계산할 수 있어야 한다.
- 적합도 함수 : 해가 얼마나 문제의 답으로 적합한지를 평가하기 위한 함수
흐름
어떤 문제에 대해 유전자 형식이 정의되었다면, 어떤 해들의 유전자들을 서로 조합함으로써 기존의 해로부터 새로운 해를 만들어낼 수 있다. 이런 조합 연산은 교배(Crossover)에 비유할 수 있다.
우수한 해들을 선택하여 이들을 교배하면, 만들어진 해는 우수한 해들이 가지는 특성을 물려받을 가능성이 높게 된다. 우수한 해의 선택에는 앞에서 정의한 적합도 함수를 이용할 수 있으며, 적합도가 높은 해가 선택될 확률을 높게 만들면, 보다 나은 유전자를 가진 해가 다음 세대에 자신의 유전자를 넘겨줄 확률이 높게 되고, 따라서 다음 세대의 해들은 최적해에 점차 가까워지게 된다. 또 비록 교배를 통해 후손을 남기지 못하더라도, 변이를 통해 새로운 유전자를 형성하여 다음 세대로 넘겨 주도록 할 수 있으며, 이는 지역 최적점에 빠지지 않도록 하는 주요한 기법이다.
해들을 교배하기 위해서는 아담과 하와처럼 초기 해의 집단이 필요하다. 초기 해 집단은 단지 이후의 해를 구하는 데 있어 필요한 초기 개체로서의 역할만을 위한 것이므로, 우수한 해들로 이루어질 필요는 없다. 일반적으로는 유전자를 랜덤하게 생성하여 초기 해 집단을 구성한다.
초기 해 집단이 구성되면, 이들 내부의 해의 교배를 통해 다음 세대의 해의 집합을 생성하게 되며, 이를 세대를 거듭하면서 반복해 가면, 해들은 점점 정답에 가까워지게 된다. 유전 알고리즘이 전역 최적해를 구하려면, 많은 인구를 유지하면서 많은 세대를 내려갈 필요가 있다. 따라서, 대부분의 경우는 세대가 일정 수준 진행되었거나, 해가 특정 범위에 들게되면 알고리즘을 종료하게 된다.
구조
유전 알고리즘은 t에 존재하는 염색체들의 집합으로부터 적합도가 가장 좋은 염색체를 선택하고, 선택된 해의 방향으로 검색을 반복하면서 최적해를 찾아가는 구조로 동작한다. 유전 알고리즘의 동작을 단계별로 표현하면 아래와 같다.
- 초기 염색체의 집합 생성
- 초기 염색체들에 대한 적합도 계산
- 현재 염색체들로부터 자손들을 생성
- 생성된 자손들의 적합도 계산
- 종료 조건 판별
- 종료 조건이 거짓인 경우, (3)으로 이동하여 반복
- 종료 조건이 참인 경우 ,알고리즘을 종료
연산
유전 알고리즘은 선택, 교차, 변이, 대치 등 몇가지 주요 연산으로 구성된다.
선택
한 세대에서 다음 세대로 전해지는 해의 후보가 되는 해들을 선택한다. 선택 방법에는 균등 비례 룰렛 휠 선택, 토너먼트 선택, 순위 기반 선택 등이 있다.
해의 선택은 유전 알고리즘의 성능에 큰 영향을 미친다. 어떤 방법을 쓰느냐에 따라 최적해로 다가가는 속도가 더디게 되거나, 아니면 지역 최적해에 빠지는 경우가 생길 수도 있기 때문이다. 또는 우수한 해가 보유한 나쁜 인자가 전체 인구에 퍼지거나, 반대로 나쁜 해가 보유한 우수한 인자가 영구히 사장될 수도 있다. 따라서 어떤 해를 선택하는지는 유전 알고리즘의 성능을 위해서 중요한 요소라고 할 수 있다.
일반적으로는 가장 좋은 해의 순으로 선택될 확률을 높게 부여하는 방법이 많이 사용된다. 이는 반대로 말하면, 나쁜 해라 할지라도 그 해에 포함된 좋은 인자를 퍼뜨릴 기회를 준다고 볼 수 있다. 현 세대에서 가장 좋은 해라 할지라도 실제로는 지역 최적해에 가까운 해일 수도 있고, 반대로 좋지 않은 해라 할지라도 전역 최적해에는 더 가까울 수도 있기 때문이다.
실제로 전역 최적해가 어디에 있는지는 알 수 없는 일이므로, 가능한 해들의 평균적인 적합도를 높여 가면서도 유전자의 다양성을 유지하는 것이 지역 최적해에 빠지는 것을 가능한 한 방지하는 방법이며, 이는 실세계의 생명체들 역시 유전적 다양성을 유지하는 종이 장기적인 생존 가능성이 높은 것과 비견할 수 있다.
교차
생명체는 세대 내에서의 교배를 통해 다음 세대를 생성한다. 이와 마찬가지로 유전 알고리즘에서 자연 선택된 해들은 교배를 통하여 다음 세대의 해들을 생성하게 된다. 일반적으로 두 개의 해를 선택한 후 둘 간에 교배 연산을 수행하게 되며, 이를 통해 생성된 해는 각각의 부모 해의 교차 연산을 통해서 서로 겹치지 않는 위치의 유전인자를 받아 새로운 유전자를 구성하게 된다.
실제 생명체의 염색체가 재조합되는 과정에서 부모 염색체의 일부분이 특정 위치를 기준으로 서로 바뀌어 결합되는 경우가 있는데, 이 현상을 교차라고 한다. 유전 알고리즘의 교차 연산은 이 현상을 본따, 부모 해의 유전자들을 서로 교차시켜서 자식해를 만들어낸다. 교차 연산의 실제 수행 방법은 비트 단위 교차에서부터 블록 단위 교차까지 다양한 방법으로 구현할 수 있으며, 교차를 한 번만 수행할지 전 영역에 대해서 교차시킬지 역시 결정할 수 있다.
또한 모든 해에 대해 교차연산을 수행할 경우 우수한 해가 다른 해와의 교배를 통해서 우수성을 잃어버림에 따라 세대의 최고 우수해가 보존되지 않는 상황이 발생할 수 있다. 이런 경우를 방지하기 위하여 교차를 확률적으로 수행하여 우수한 해가 변형되지 않고 그대로 다음 세대에 전해질 확률을 부여하는 방법도 사용된다.
변이
일반 생명체에서, 유전자의 교배 뿐 아니라, 하나의 유전자가 직접적으로 변이를 일으켜서 주어진 환경에서 살아남을 확률 역시 존재한다. 변이 연산은 주어진 해의 유전자 내의 유전 인자의 순서 혹은 값이 임의로 변경되어 다른 해로 변형되는 연산이다.
해의 유전자들을 가상의 공간에 맵핑할 경우 교배 연산은 부모해들 사이의 어떤 지점에 자식해를 생성하는 것이라고 볼 수 있다면, 변이 연산은 임의의 위치로 점프하는 것에 비견할 수 있다. 따라서 약간의 확률로 변이 연산을 수행시켜 주는 것은 전체 세대가 함께 지역 최적해에 빠져드는 경우를 방지하기 위한 주요한 기법이 될 수 있으며, 해집단의 다양성을 높여준다.
대치
교차·변이 등을 거쳐서 만들어진 새로운 해를 해집단에 추가하고, 기존 해 중 열등한 해를 가려내서 제외시키는 연산이다. 가장 품질이 나쁜 해를 대치하는 방법, 새로운 해의 부모해 중에서 새로운 해와 가장 비슷한 해를 대치시키는 방법(해집단의 다양성을 유지하기 위함) 등이 있다.
특징
대부분의 전통적 최적화 방법은 지금까지 발견된 가장 좋은 한 개의 해결 방법을 가지고 탐색해 나가는 데에 비하여, 유전자 알고리즘은 후보 해결 방법들의 모집단을 갖고 탐색해 나간다.
물론 현재의 모집단에서 가장 좋은 해결 방법은 오직 한 개 혹은 동등한 목적 함수 값을 갖는 몇 개일 것이다. 그러나 다른 해결 방법들은 현재는 좋은 방법이 아니지만 검색공간의 다른 영역에 있는 샘플 포인트로서 향후 그 영역에서 보다 나은 해결 방법을 찾을 수 있도록 하는 거점 역할을 한다. 즉, 해결 방법의 모집단을 사용함으로써 유전자 알고리즘이 로컬 최적화(localoptima)에 빠지는 위험을 방지할 수 있다.
장단점
- 장점
- 기울기 정보를 필요로 하지 않아, 함수에 연속이거나 미분가능성 등의 제약을 받지 않아 연속적 변수와 불연속적 변수들이 함께 섞여 있는 문제를 해결하는 데 적합하다.
- 로컬 최적화를 피해갈 수 있는 전반적인 매커니즘을 가지고 있다.
- 복수의 개체 사이에서 선택이나 교배 등의 유전적 조작에 의해, 상호 협력적으로 해의 탐색을 수행하고 있다. 따라서, 단순한 병렬적 해의 탐색과 비교하여 보다 좋은 해를 발견하기 쉽다.
- 인공 신경망(Neural Network), 특히 역전파 알고리즘 등에서는 평가 함수의 미분값을 필요로 하였다. 유전자 알고리즘에서는 현재 적응도를 분별할 수 있으면 되기 때문에 알고리즘이 단순하고, 평가 함수가 불연속인 경우에도 적용이 가능하다.
- 단점
- 유전자 알고리즘에서 도출한 최적 방법은 다른 방법에 비교하여 좋다는 의미일 뿐, 실제로 ‘최적’의 해결 방법이라는 개념은 포함하지 않는다. 즉, 어떤 도출된 해결 방법이 최적임을 검증할 방법이 없다.
- 현실 세계에 존재하는 문제 중 대상으로 하는 문제를 유전자형으로 바꾸는 과정이 간단하지 않다.
- 개체 수, 선택 방법, 교차의 결정, 돌연변이 비율, 최적화 함수 등 결정해 줘야 하는 변수가 많고, 그에 따른 결과 차이가 크다.
단계
대부분의 유전자 알고리즘은 모집단을 갖고 그 모집단에서 먼저 n개의 해를 생성한다. 그리고 그 n개의 해에서 선택(selection), 교차(crossover), 변이(mutation)의 단계를 거쳐서 새로운 k개의 해를 생성하게 된다. 이렇게 만들어진 k개의 해는 기존에 있던 모집단에서 k개의 해를 대체해서 새로운 해가 된다. 이런 과정이 반복 조건을 만족할 때까지 계속 되고 모집단에 남은 해 중 가장 적합한 해가 최적해가 된다. 위와 같은 과정을 단계별로 살피면 다음과 같다.
유전자형 결정
- 스키마 : 문제를 유전자형으로 표현하기 위해서는 우선 스키마(scheme)의 개념을 알아야 한다. 스키마는 염색체에서 나타날 수 있는 패턴을 말한다. 예를 들어, 염색체가 모두 3자리의 ‘100’으로 이뤄졌다고 했을 때, 이 염색체는 100,1,0,10,10,00,***의 8개의 부분 패턴을 포함하고 있어, 8개의 스키마를 가지고 있는 것이다. 이진수로 표현된 염색체의 경우, 자리수가 n이라고 할 때 모두 2^n개의 스키마를 갖는다.
- 이진수 표현과 n진수 표현 : 문제의 해가 될 수 있는 것을 유전자형으로 표현하는 방법은 여러가지가 있는데, 존 홀랜드는 문제의 해를 유전자형으로 표현하기 위해 이진수(binary) 표현을 사용하였다. 이진수 표현 방법이 스키마 처리에 용이하단 이유에서이다. 그러나 이진수 표현 방법 외에 n진수(n-nary)로 문제를 해결하는 방법도 있다. 이진수로 표현할 경우, 교차할 때 추가변이 효과가 생겨 교차의 다양성을 기대할 수 있다. 또한 n진수로 표현할 경우는 의미 있는 스키마를 보존할 가능성이 높아진다.
- 실수 표현 : 유전자를 한 실수로 지정하는 실수 표현 방법으로도 유전자형 변환이 가능하다. 실수 표현은 독일의 진화 전략(Evolution Strategy)에 의해 발전했다. 실수 표현은 유전자로 변환하고자 하는 인자가 실수일 경우, 그대로 유전자형으로 가져다 쓸 수 있어 매우 간편하다.
- 그 밖의 표현 : 위의 두 방법 이외에도 유전자들의 현재 위치가 의미를 갖는 위치 기반 표현, 현재 위치는 아무 의미도 없고 상대적인 순서들로 표현되는 순서 기반 표현과 유전자를 1차원으로 표현했을 때 생기는 정보 손실을 막기 위한 다차원 표현 방법 등 여러가지 표현 방법이 있다.
초기 모집단 결정
유전자 알고리즘에서 모집단은 염색체 간의 상호작용을 위해 매우 중요하다. 모집단의 크기는 초반에 지정해아 한다. 만약 모집단의 크기가 너무 작을 경우 염색체의 숫자도 적어져, 교차를 통한 진화를 목적으로 유전자 알고리즘의 장점을 제대로 활용할 수 없다.
모집단의 크기가 너무 크다면 한 세대에 너무 많은 연산을 필요로 하기 때문에 유전자 알고리즘의 속도가 저하될 수 있다. 유전자형 표현과 마찬가지로 설계자의 경험에 의한 적절한 모집단 크기 결정이 필요하다.
개체 적합도
계산초기 모집단에 존재하는 유전자들은 우리가 찾고자 하는 해에 가깝기만 하고 해가 될 수는 없는 부족한 유전자일수도 있다. 초기 세대에 이런 유전자를 이용해서 알고리즘을 진행하면 그 다음 세대까지 영향을 받게 되어서, 우리가 찾고자 하는 다른 적합도 높은 유전자를 발견하지 못할 수도 있다.
이것을 막기 위해 각 개체의 적합도를 평가하기 위해서는 평가함수를 구해야 한다. 그런데 구하고자 하는 문제에 따라서 평가 함수의 구간값이 다르기 때문에, 구간 사이의 표준화된 값을 정해서 새로운 적합도 함수를 구해 이것을 개체 선택에 이용해야한다. 원래의 구간값을 새로운 표준화된 값으로 바꾸는 방법은 여러 가지가 있지만, 다음이 대표적인 방법들이다.
f : 표준화 전의 적합도 값
f' : 표준화 후의 적합도 값- 선형 표준화 :
f’ : af + b의 식으로 실행하며, 선형표준화에서 적합도 값이 음수가 되지 않도록 수를 조정해 줘야 한다. - 거듭제곱 표준화 :
f’ : f^k으로 실행하며, k값은 문제에 따라 가변적이다. - a 절단 :
f’ = f - (m - a)의 식에 의해 시행되며, 시그마 절단 방법에서 표준화후의 적합도가 음수가 되는 경우에는 이를 0으로 바꿔줘야 한다. 모집단의 각 개체의 적합도를 검사하며, 적합도 검사 결과 해(solution)로서 만족하는 개체가 있으면 알고리즘이 종료되지만 만족하는 개체가 없을 경우에는 다음 단계로 넘어간다.
선택 수행
선택 과정에서는 우수 유전자가 생존에 유리한 자연 선택과정과 유사하게 진행되는데, 여러가지 선택 방법들의 적합도 함수에 의해 계산된 유전자 중, 해에 가까운 유전자들에게 좀 더 높은 선택 확률을 준다는 공통점을 가지고 있다.
- 룰렛 선택 : 룰렛 선택은 적합도 비례 방법이라고도 한다. 각 유전자의 적합도에 따라 선택될 확률을 k배로 조정하는 방법이다. 룰렛 방법은 각각의 유전자가 룰렛 위의 적합도만큼의 공간을 차지하고 있다고 가정한다. 그 후에 화살을 쏘았을 때 선택 확률은 룰렛 위에 유전자가 차지하고 있는 공간에 비례하게 된다. 확률에 기반하였기 때문에 우수한 개체라도 선택되지 않을 가능성이 있으며 열등한 개체라도 선택될 가능성이 있다. 그러나 모집단 내의 개체수가 적을 경우, 선택되는 개체의 분포에 다양하지 않다는 한계가 있다.
- 기대값 선택 : 적합도에 대한 각 개체의 기대값을 구하고 그 값에 따라 확률적인 재생 개수를 구하여 선택하는 방법이다. 기대값 선택의 경우, 한 번 선택된 개체가 반복해서 선택될 가능성이 있기 때문에 한 번 선택된 개체수는 기대값을 곱해 줘서 다시 뽑힐 확률을 최소화시킨다.
- 순위 기반 선택 : 룰렛 선택 방법은 확률에 따라 개체의 선택여부가 결정되기 때문에 우수한 개체가 많이 선택된다는 장점도 있지만 특정 개체들만 선택될 가능성도 있다. 순위 기반 선택 방법은 그걸 보완하여 적합도에 따라 순위를 매기고, 그 순위에 따라 확률을 결정하는 방법이다.
- 토너먼트 선택 : 개체군 중에서의 임의의 개체들을 선택해서 비교한 다음에, 그 중에 적합도가 더 높은 개체를 다음 세대에 남기는 선택 방법이다. 그렇게 선택된 개체를 또 다른 개체와 계속 비교한 다음에 그 중에서 적합도가 높은 개체를 남기게 되는 방식이 토너먼트 방식과 유사하여 토너먼트 선택 방법이라 한다.
- 엘리트 보존 방법 : 확률에 따라 개체를 선택하게 될 때, 우수한 개체가 소실되는 것을 막기 위해 가장 좋은 해를 보존하여 다음 세대에 넘기는 선택 방법이다. 보통 다른 방법과 함께 사용된다.
교차 처리
부모 염색체를 부분적으로 바꾸어 자식의 염색체를 생성하는 방법
- 일점 교차 교차하는 위치를 한 군데 결정하고, 그 앞과 뒤에서 어느 쪽의 유전자형을 받을 것인가를 결정하여 변경시키는 방법으로 가장 일반적인 교차 방법이다.
P1: a b c d e f g h i j P2: k l m n 0 ↓ p q r s t S1: a b c d e p q r s t S2: k l m n o f g h i j - 복수점 교차 교차 위치가 복수인 방식이다. 예를 들어 교차 위치가 2와 5라면 새로운 개체의 하나는 개체 A의 선두로부터 두 번째까지, 개체 A의 세 번째로부터 다섯 번째까지, 개체 의 여섯 번째부터 마지막까지 유전자가 만들어진다. 동시에 그 반드의 조합에 의해서 또 다른 하나의 새로운 개체의 유전자가 만들어진다.
P1: a b c d e f g h i j P2: k l m n o p q r s t S1: a b c n o p q r s t S2: k l m d e p q h i j - 균일 교차 위의 방법과 같이 지름선을 사용하지 않고, 특정한 마스크를 사용하여 P1과 P2에서 가져오는 유전자를 결정하는 방식이다. 마스크의 값이 0일 경우는 P1에서 가져오고, 1일 경우는 P2에서 값을 가져온다. 일점 교차나 복수점 교차에 비해 스키마의 결합 형태가 다양하고, 그만큼 수렴 시간이 오래 걸린다.
P1: a b c d e f g h i j P2: k l m n o p q r s t M0: 0 1 1 0 1 0 1 1 0 0 S1: a l m d o f q r i j S2: k b c n e p g h s t - 변이 수행 변이는 유전자를 일정한 확률로 변화시키는 조작이다. 돌연변이를 너무 큰 변이 확률로 설정하면 적합도가 떨어지는 경우도 생기게 되지만 오히려 적합도가 높아지는 경우도 생긴다. 초기에는 품질이 좋지 않은 해가 많으므로 변이의 강도를 높이는 게 좋으며, 후반에 가서는 품질 향상에 변이가 큰 영향을 미치지 않으므로 강도를 낮춰 준다. 변이는 개체군의 다양성을 유지하여 국지 최적해(localminimum)에 빠질 위험을 배제한다. 그러나 변이의 확률이 높아지면 수렴성이 떨어져 수행 시간이 많이 걸리게 된다.
유전 알고리즘을 활용한 TSP
With 완전탐색
import pandas as pd
from itertools import permutations
def solution(dist_table):
print(len(dist_table),len(dist_table[0]))
temp = [i for i in range(9)]
min_val = 999999999
min_subject = []
subject_iter = permutations(temp) # len : 362880
for subject in subject_iter:
val = 0
prev_node = subject[0]
for i in range(1,9):
node = subject[i]
val += int(dist_table[prev_node][node])
prev_node = node
val += int(dist_table[subject[8]][subject[0]])
if val < min_val:
min_val = val
min_subject = subject
print("최단 경로 : " + str(min_subject))
print("최단 거리 : " + str(min_val))
# 최단 경로 : (0, 1, 2, 8, 7, 6, 5, 4, 3)
# 최단 거리 : 1018
def main():
df = pd.read_excel('distance.xlsx',header=1,usecols=range(1,10))
dist_table = df.values.tolist()
solution(dist_table)
if __name__ == "__main__":
main()
출력값

With 유전 알고리즘
import random
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from statsmodels.formula.api import ols
POPULATION_SIZE = 16 # 개체 집단의 크기
MUTATION_RATE = 0.2 # 돌연 변이 확률
SIZE = 9 # 하나의 염색체에서 유전자 개수
df = pd.read_excel('distance.xlsx',header=1,usecols=range(1,10))
dist_table = df.values.tolist()
TARGET_VAL = 1018
# 최단 경로 : (0, 1, 2, 8, 7, 6, 5, 4, 3)
# 최단 거리 : 1018
class Chromosome:
def __init__(self, g = []):
self.genes = g
self.fitness = 0
if self.genes.__len__()==0:
temp_list = list(range(9))
random.shuffle(temp_list)
self.genes = temp_list.copy()
def cal_fitness(self): # 적합도를 계산
global dist_table
self.fitness = 0
value = 0
prev_node = self.genes[0]
for i in range(1,9):
node = self.genes[i]
value += int(dist_table[prev_node][node])
prev_node = node
value += int(dist_table[self.genes[8]][self.genes[0]])
self.fitness = TARGET_VAL * 2 - value if TARGET_VAL * 2 - value > 0 else 1
return self.fitness
def __str__(self):
return self.genes.__str__()
def print_p(pop):
i = 0
for x in pop:
print("염색체 #", i, "=", x, "적합도=", x.fitness)
i += 1
print("")
# 선택 연산
def select(pop):
max_value = sum([c.cal_fitness() for c in population])
pick = random.uniform(0, max_value)
current = 0
for c in pop:
current += c.cal_fitness()
if current > pick:
return c
# 교차 연산
def crossover(pop):
father = select(pop)
mother = select(pop)
length = random.randint(1, SIZE - 1)
idx = random.randint(0, SIZE - length)
t_child1 = mother.genes[idx:idx + length].copy()
t_child2 = father.genes[idx:idx + length].copy()
child1 = list(filter(lambda x: not x in t_child1,father.genes))
child2 = list(filter(lambda x: not x in t_child2,mother.genes))
child1 = child1[:idx] + t_child1 + child1[idx:]
child2 = child2[:idx] + t_child2 + child2[idx:]
return (child1, child2)
# 돌연변이 연산
def mutate(c):
if random.random() < MUTATION_RATE:
x, y = random.sample(list(range(0,9)),2)
c.genes[y], c.genes[x] = c.genes[x], c.genes[y]
# 메인 프로그램
population = []
i=0
fitness_list = []
# 초기 염색체를 생성하여 객체 집단에 추가한다.
while i<POPULATION_SIZE:
population.append(Chromosome())
i += 1
count=0
population.sort(key=lambda x: x.cal_fitness(),reverse=True)
print("세대 번호=", count)
print_p(population)
count=1
max_fitness = 0
while population[0].fitness < TARGET_VAL:
if population[0].fitness > max_fitness:
MUTATION_RATE = MUTATION_RATE * 0.9
max_fitness = population[0].fitness
new_pop = []
# 선택과 교차 연산
for _ in range(POPULATION_SIZE//2):
c1, c2 = crossover(population)
new_pop.append(Chromosome(c1))
new_pop.append(Chromosome(c2))
# 자식 세대가 부모 세대를 대체한다.
# 깊은 복사를 수행한다.
population = new_pop.copy()
# 돌연변이 연산
for c in population: mutate(c)
# 출력을 위한 정렬
population.sort(key=lambda x: x.cal_fitness(),reverse=True)
fitness_list.append(population[0].fitness)
print("세대 번호=", count)
print_p(population)
count += 1
if count > 50000 : break
x, y = range(len(fitness_list)),fitness_list
fit_line = np.polyfit(x,y,1)
x_minmax = np.array([min(x), max(x)])
fit_y = x_minmax * fit_line[0] + fit_line[1]
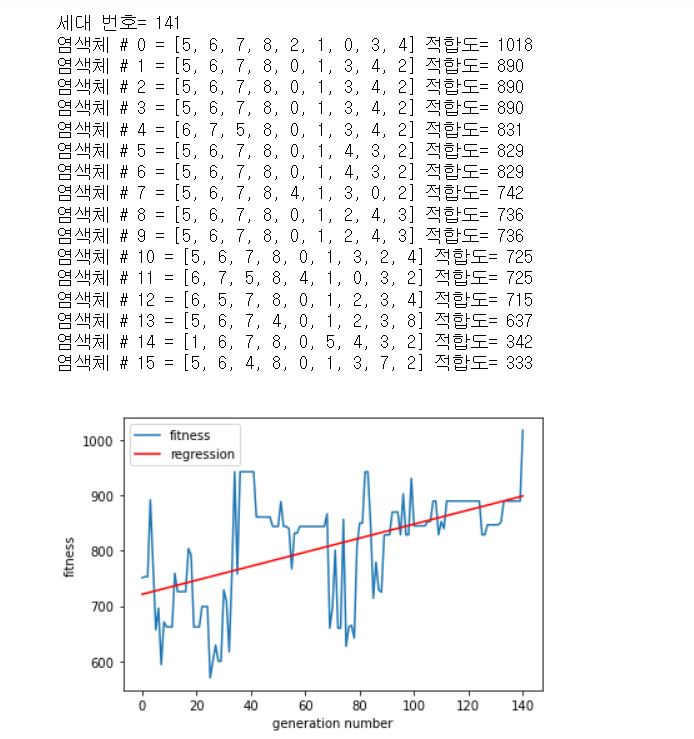
plt.plot(fitness_list,label='fitness')
plt.plot(x_minmax, fit_y, color = 'red',label='regression')
plt.xlabel('generation number')
plt.ylabel('fitness')
plt.legend()
plt.show()