[Algorithm] Sorting Algorithms

Sorting Algorithms은 말 그대로 정렬되지 않은 리스트를 오름차순, 혹은 내림차순으로 정렬하는 알고리즘입니다. 그 종류는 다양한데, 이 포스팅에서 소개할 내용은 다음과 같습니다. 옆에 표시된 것은 각각의 시간복잡도입니다! 적재적소에 사용하면 됩니다.

1. Bubble Sort (버블정렬) -> O(n^2)
2. Selection Sort (선택정렬) -> O(n^2)
3. Insertion Sort (삽입정렬) -> O(n^2)
   
   
4. Quick Sort (퀵정렬) -> O(n*logn)
5. Merge Sort (병합정렬) -> O(n*logn)
6. Heap Sort (힙정렬) -> O(n*logn)
   
   
7. Radix Sort (기수정렬) -> O(n)
8. Counting Sort (계수정렬) -> O(n)

1. Bubble Sort

Bubble Sort (버블정렬)은 인접한 두 개의 원소를 비교하여 자리를 교환하는 방법입니다. 첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 마지막 자리로 이동하는 모습이 물 속에서 물 위로 올라오는 물방울 모양과 같다고 하여 지어진 이름이라고 합니다. 작동 원리는 아래 그림과 같습니다.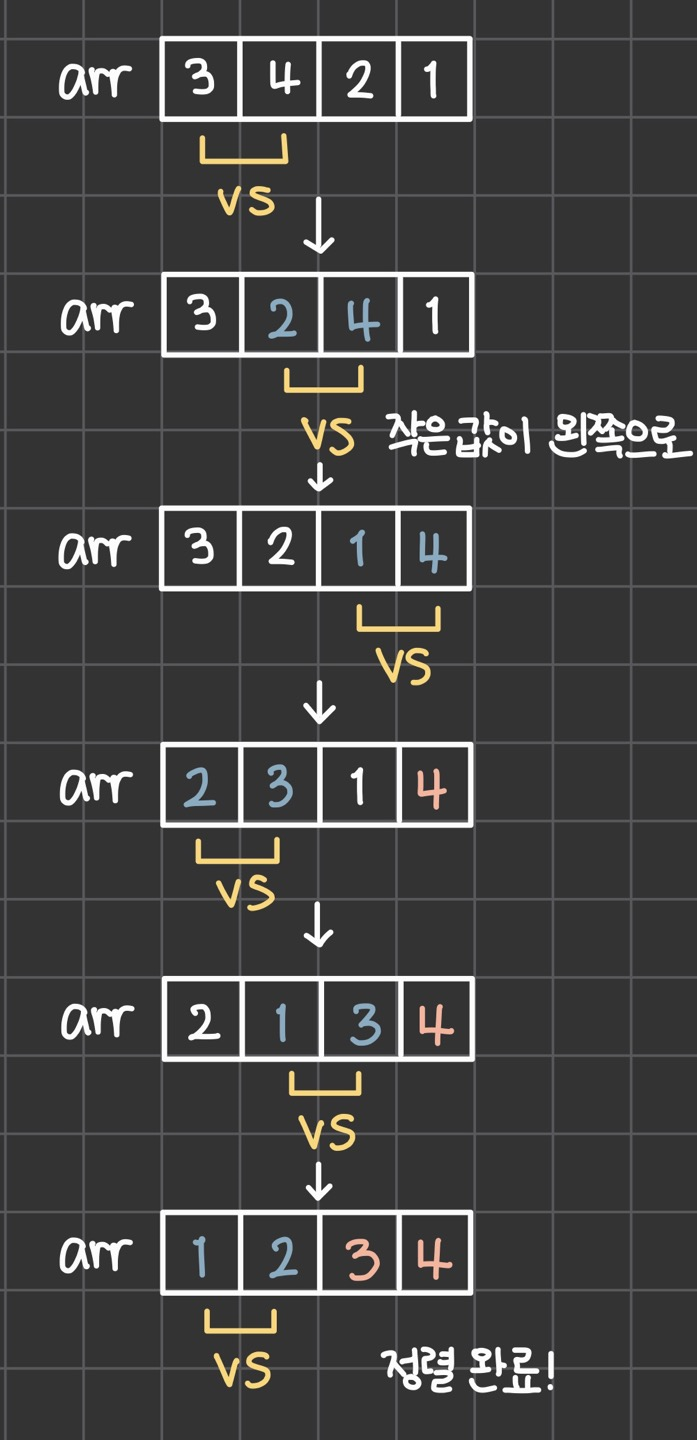 위 사진처럼 인접한 두 개의 원소를 비교하여 swap하는 과정을 반복하는 알고리즘입니다. 이를 코드로 구현하면 다음과 같습니다.

void BubbleSort (int arr[], int n) {
    for (int i = 0; i < n-1; i++) {
    	for (int j = 0; j < (n-i)-1; j++) {
        	if (arr[j] > arr[j+1]) {	//데이터 교환 조건
                swap(arr[j] , arr[j+1]);
            }
        }
    }
}

int main() {
	int arr[4] = {3, 4, 2, 1};
    BubbleSort(arr, sizeof(arr)/sizeof(int));
    
    for (int i = 0; i < 4; i++)
    	printf("%d ", arr[i]);
}

i번째 원소를 (n-i)번 비교하므로, 비교횟수 : n(n-1)/2
최악의 경우, i번째 원소를 (n-i)번 교환하므로, 자리교환횟수 : n(n-1)/2
따라서 시간복잡도는 O(n^2) 입니다.

2. Selection Sort

Selection Sort (선택정렬)은 최솟값을 찾아 맨 앞의 값과 바꾸는(swap) 방법입니다. 배열의 시작주소와 원소의 개수를 인자로 받습니다.
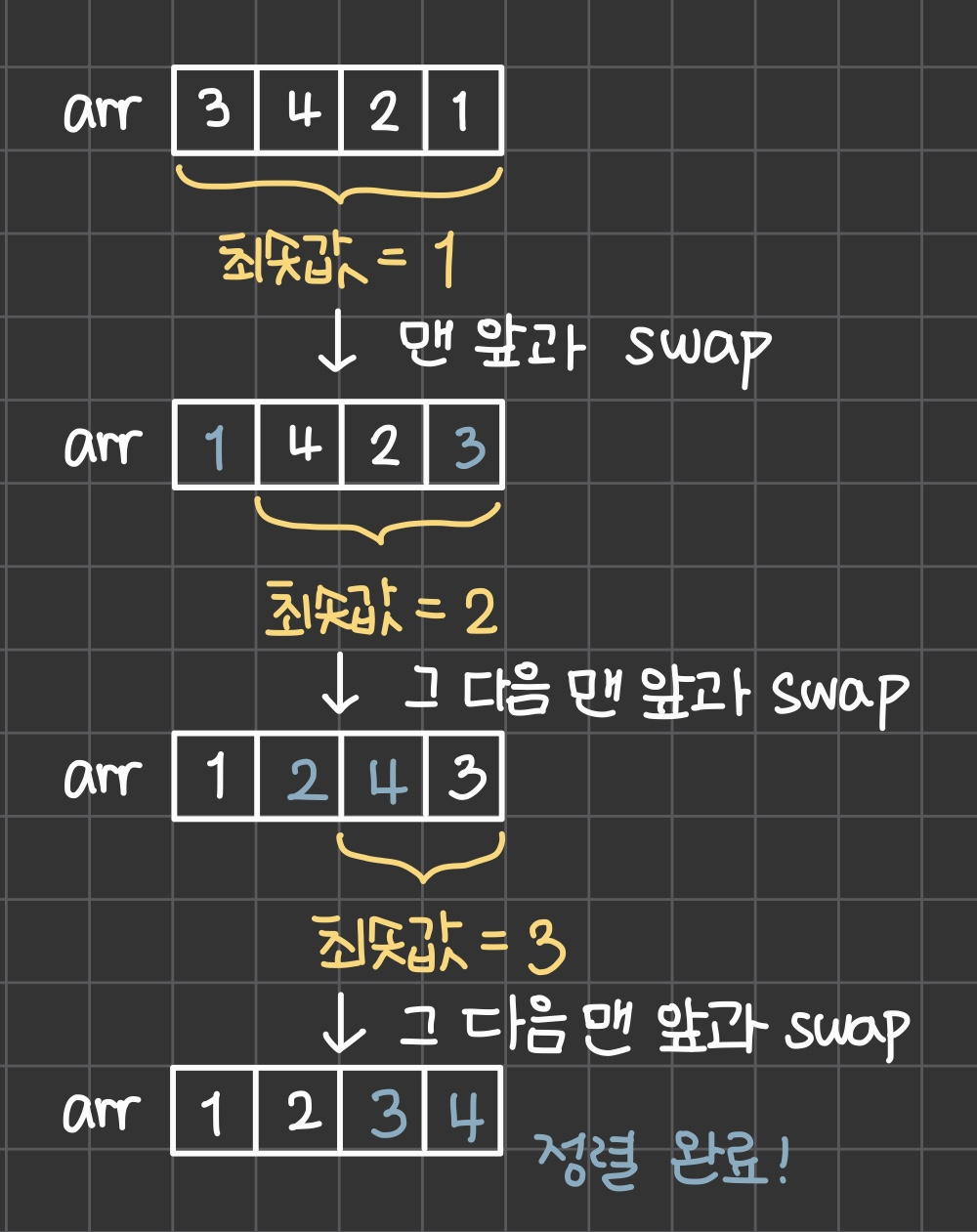위 사진처럼 최솟값을 찾아 맨 앞과 swap하는 과정을 반복하는 알고리즘입니다. 이를 코드로 구현하면 다음과 같습니다.

void SelectionSort (int *arr, const int cnt) {
    for (int i = 0; i < cnt; i++) {
        int j = i;

        for (int k = i+1; k < cnt; k++)
            if (arr[k] < arr[j]) j = k;
        
        swap(arr[i], arr[j]);
    }
}

i번째 원소를 기준으로 n-i개의 원소를 비교하므로,
비교횟수 : (n-1) + (n-2) + ... + (n-(n-1)) = n(n-1)/2
따라서 시간복잡도는 O(n^2) 입니다.

3. Insertion Sort

Insertion Sort (삽입정렬)은 정렬되어 있는 부분집합에 정렬할 새로운 원소의 위치를 찾아 삽입하는 방법입니다.
정렬할 자료를 두 개의 부분집합 S (정렬된 앞부분의 원소들), U (아직 정렬되지 않은 나머지 원소들)를 사용합니다. U의 원소를 하나씩 꺼내서 S의 마지막 원소부터 비교하면서 위치를 찾아 삽입합니다.
최종적으로, U가 공집합이 되면 삽입 정렬이 완성됩니다. 작동 원리를 아래 그림으로도 살펴보겠습니다.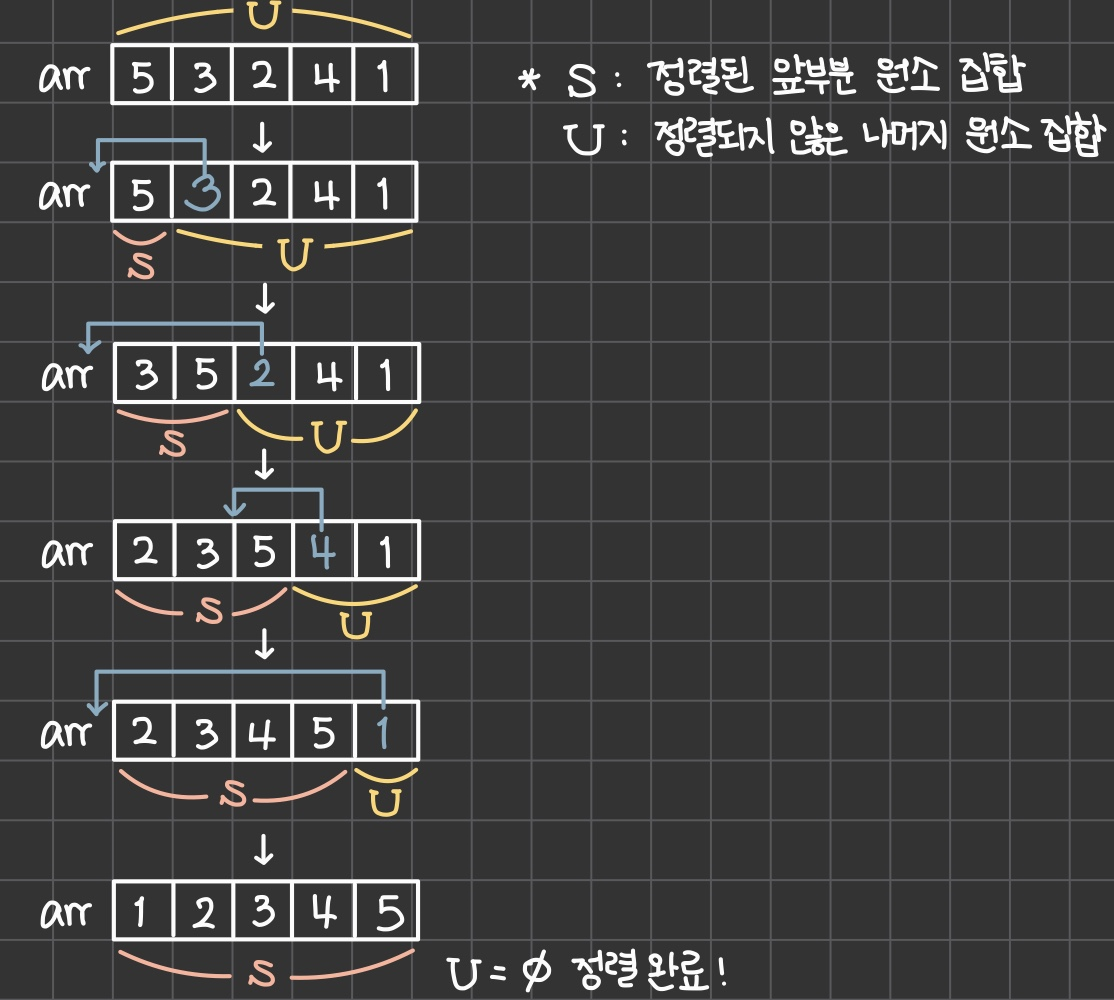이를 코드로 구현하면 다음과 같습니다.

void Insertionsort ( int arr[], int n) {
	int insData;
    
    for (int i = 1; i < n; i++) {
    	//arr[0]은 이미 S에 있음. i는 1부터!
    	insData = arr[i];	//U에 있는 정렬할 원소
        int j;
        for (j = i-1; j >= 0; j--) {
        	if (arr[j] > insData)
            	arr[j+1] = arr[j];	//비교대상 뒤로 한 칸 밀기
            else break;
        }
        arr[j+1] = insData;
    }
}

int main() {
	int arr[5] = {5, 3, 2, 4, 1};
    InsertionSort(arr, sizeof(arr)/sizeof(int));
    
    for (int i = 0; i < 5; i++)
    	printf("%d ", arr[i]);
}

최악의 경우, 전체 비교횟수 : 1+2+3+ ... +(n-1) = n(n-1)/2
따라서 시간복잡도는 O(n^2) 입니다.

4. Quick Sort

Quick Sort (퀵정렬)은 기준값(pivot)을 중심으로 왼쪽 부분집합과 오른쪽 부분집합으로 분할하여 정렬하는 방법입니다. 왼쪽 부분 집합에는 기준값보다 작은 원소들을 이동시키고, 오른쪽 부분 집합에는 기준값보다 큰 원소들을 이동시키는 과정이 반복됩니다. 즉, 아래 두 가지 작업을 반복 수행하여 완성합니다.

분할 정복(divide and conquer) 기법

• 분할 (divide)
  정렬할 자료들을 기준값을 중심으로 2개의 부분집합으로 분할
• 정복 (conquer)
  왼쪽, 오른쪽 부분집합으로 각각 정렬
  부분집합의 크기가 1 이하로 충분히 작지 않으면 다시 분할

작동 원리를 아래 그림으로도 살펴보겠습니다.
이를 코드로 구현하면 다음과 같습니다.

void QuickSort (int arr[], const int left, const int right) {
    if (left < right) {
        int low = left + 1;
        int high = right + 1;
        int pivot = arr[left];
        
        while (1) {
            do low++; while (arr[low] < pivot && low <=right);
            do high--; while (arr[high] > pivot && high >= left);
            if (low >= high) break;
            swap(arr[low], arr[high]);
        }

        swap(arr[left], arr[high]);

        QuickSort(arr, left, high - 1);
        QuickSort(arr, high + 1, right);
    }
}

int main() {
    int arr[9] = {5, 1, 3, 7, 9, 2, 4, 6, 8};
    QuickSort(arr, 0, 8);

    for (int i = 0; i < 9; i++)
        printf("%d ", arr[i]);
}

최선의 경우 (완전 이진 트리), 정확히 n/2개씩 이등분이 되는 경우가 반복됩니다.
최악의 경우 (편향 이진 트리), pivot에 의해 원소들을 분할하였을 때 1개와 (n-1)개로 분할되는 경우가 전체 원소의 개수만큼 반복됩니다.
따라서 평균 시간복잡도는 O(n*logn) 입니다.
하지만, 최악의 경우 pivot을 잘못 선택하면 시간복잡도가 O(n^2)까지 갈 수 있으니 사용 시 주의하시기 바랍니다!

5. Merge Sort

Merge Sort (병합 정렬)은 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방법입니다. Quick Sort와 마찬가지로, 분할정복(divide and conquer)기법을 사용합니다.

분할 정복 기법

• 분할(divide) : 입력 자료를 같은 크기의 부분집합 n개로 분할
• 정복(conquer) : 부분집합의 원소들을 정렬
• 결합(combine) : 정렬된 부분집합들을 하나의 집합으로 결합

Merge Sort의 종류

• 2-way 병합 : 2개의 정렬된 자료의 집합을 결합하여 하나의 집합으로
• n-way 병합 : n개의 정렬된 자료의 집합을 결합하여 하나의 집합으로

작동 원리를 아래 그림으로도 살펴보겠습니다.이를 코드로 구현하면 다음과 같습니다.

void MergeSort (int[], int, int);
void MergeTwoArea (int[], int, int, int);

int main() {
    int arr[8] = {5, 1, 3, 7, 8, 2, 4, 6};

    MergeSort(arr, 0, 7);

    for (int i = 0; i < 8; i++)
        printf("%d ", arr[i]);
    
    printf("\n");
}

void MergeSort (int arr[], int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
		
        // 두 개의 영역으로 분할
        MergeSort(arr, left, mid);
        MergeSort(arr, mid + 1, right);

        MergeTwoArea(arr, left, mid, right);
    }
}

void MergeTwoArea (int arr[], int left, int mid, int right) {
    int fIdx = left;
    int rIdx = mid + 1;

    // 병합 결과를 담을 메모리 할당
    int *sortArr = new int[right+1];
    int sIdx = left;

    // 병합할 두 영역의 데이터 비교 후, sortArr에 담기
    while (fIdx <= mid && rIdx <= right) {
        if (arr[fIdx] <= arr[rIdx])
            sortArr[sIdx] = arr[fIdx++];
        else
            sortArr[sIdx] = arr[rIdx++];
        sIdx++;
    }

    // 한 쪽의 데이터가 모두 이동되어 나머지 데이터를 sortArr로 이동
    if (fIdx <= mid) 
        copy(arr + fIdx, arr + (mid+1), sortArr + sIdx);
    else if (rIdx <= right)
        copy(arr + rIdx, arr + (right+1), sortArr + sIdx);

    // 합병 결과 기존의 배열에 옮겨 담기
    for (int i = left; i <= right; i++) {
        arr[i] = sortArr[i];
    }

    // 메모리 해제 (참고로, 메모리 할당, 해제는 시간이 많이 소요돼 비효율적임.)
    delete(sortArr);
}

Merge Sort(병합 정렬)은 각 단계에서 새로 병합하여 만든 부분집합을 저장할 공간이 추가로 필요합니다. 그렇기에 (n2)개의 공간을 사용합니다.
시간복잡도를 분석해보겠습니다. 분할 단계에서, n개의 원소를 분할하기 위해 O(logn)의 시간이 소요되고, 병합 단계에서 이러한 비교연산이 최대 n번 수행되기 때문에 전체적인 시간복잡도는 O(nlogn)을 가집니다.

6. Heap Sort

Heap Sort(힙 정렬)은 Merge Sort(병합 정렬)의 단점을 보완한 정렬입니다.
Merge Sort의 대표적인 단점으로는, 정렬할 레코드 수에 비례하여 저장공간이 추가로 필요하다는 점입니다. 이를 보완한 Heap Sort는 상수 공간만큼만 사용하면서 동일한 시간복잡도(O(nlog))를 가지고 있습니다. 동일한 시간복잡도를 가지고 있지만, Merge Sort에 비해 아주 약간 느리다고 합니다.
추가로, 다루진 않겠지만 O(1)의 추가공간을 사용하는 Merge Sort가 있다고 하는데요! 이보단 빠르다고 합니다.
Heap Sort는 최대-힙 구조를 사용합니다. Adjust 함수를 사용하여 일정한 양의 저장공간만 필요하도록 최대 힙을 재조정하는 과정을 거칩니다. 삭제, 삽입 함수로 최대-힙 구조를 사용하기 때문에 O(nlogn)의 시간복잡도를 갖습니다.
그렇다면 Heap이란 무엇을 의미하는 걸까요? Heap의 의미부터 알아보겠습니다.

Heap(힙) : 완전 이진 트리에 있는 노드 중에서 key값이 가장 큰/작은 노드를 찾기 위한 자료구조

• Max Heap(최대 힙)
  - key값이 가장 큰 노드를 찾기 위한 완전 이진 트리
  - 부모노드의 key값 >= 자식노드의 key값
  - root 노드 : key값이 가장 큰 노드
• Min Heap(최소 힙)
  - key값이 가장 작은 노드를 찾기 위한 완전 이진 트리
  - 부모노드의 key값 <= 자식노드의 key값
  - root 노드 : key값이 가장 작은 노드

이제 좀 Heap에 대해 감이 오시나요? Heap Sort는 위에서 얘기했던 바와 같이, 최대-힙 자료구조 이용하는 정렬 방법입니다.

Heap Sort 수행 과정
1) 정렬할 원소들을 입력하여 최대 힙 구성
2) 힙에 대해서 삭제 연산을 수행하여 얻은 원소(root 노드의 원소)를 마지막 자리에 배치
3) 나머지 원소에 대해 다시 최대 힙으로 재구성 -> 원소 개수만큼 2)~3) 반복

Heap Sort에서 쓰이는 Adjust함수는 바로, 3)번 과정(최대 힙 구조 재구성)을 위해 쓰이는 함수입니다. Heap의 첫 번째 레코드와 마지막 레코드를 교환한 후, Heap의 크기를 줄인 후 Heap을 재조정하는 것이죠! Adjust의 연산 시간은 O(d)입니다!(단, d는 트리의 깊이)
작동 원리를 아래 그림으로도 살펴보겠습니다.

이를 코드롤 구현하면 다음과 같습니다.

7. Radix Sort

8. Counting Sort

참고하면 좋은 사이트

• 정렬 관련 백준 문제 풀기
  https://www.acmicpc.net/problemset?sort=ac_desc&algo=97
• 정렬 관련 애니메이션 보기
  https://www.toptal.com/developers/sorting-algorithms