[파일처리] 직접 화일

직접 화일

• 임의 접근 화일
  • 임의의 레코드 키 값으로 레코드 직접 접근 가능
  • 직접 화일, 직접 접근 화일 (↔ 순차접근화일)
  • 다른 레코드 참조 X
• 종류
  1. 인덱스된 화일
     • 인덱스를 이용한 레코드 접근
  2. 인덱스된 순차 화일
     • 인덱스를 이용한 임의 접근/순차 접근 모두 지원
  3. 상대 화일
     • 키와 화일 내 레코드의 상대적 위치 사이에 정해진 관계 이용
  4. 해시 화일
     • 키 값을 레코드 주소로 변환
     • 협의의 직접 화일

상대 화일

• 상대 화일
  • 레코드 키와 화일 내 레코드 위치(상대 레코드 번호) 사이 관계 이용
• 상대 레코드 번호
  • 화일이 시작되는 첫 번째 레코드 기준
  • RNN : 상대 주소
  • 물리적 정렬 필요 X
• 사상 함수
  • A : 키 값 → 주소
  • 상대 화일은 메인 메모리, 디스크(직접 저장 장치)에 저장하는 것이 효율적
  • 구현방법
    1. 직접 사상
    2. 디렉터리 검사
    3. 계산을 이용한 방법 (해싱)
• 직접 사상
  • 절대 주소 = 키 값 → <실린더 번호, 면 번호, 블록 번호>
    
  • 장점
    • 키 값 → 주소 변환 과정 간단
    • 처리 시간 X
  • 단점
    • 물리적 저장장치에 전적으로 의존
    • 물리적 데이터 독립성 결여 → 논리 주소 = 물리 주소
      
• 디렉터리 검사

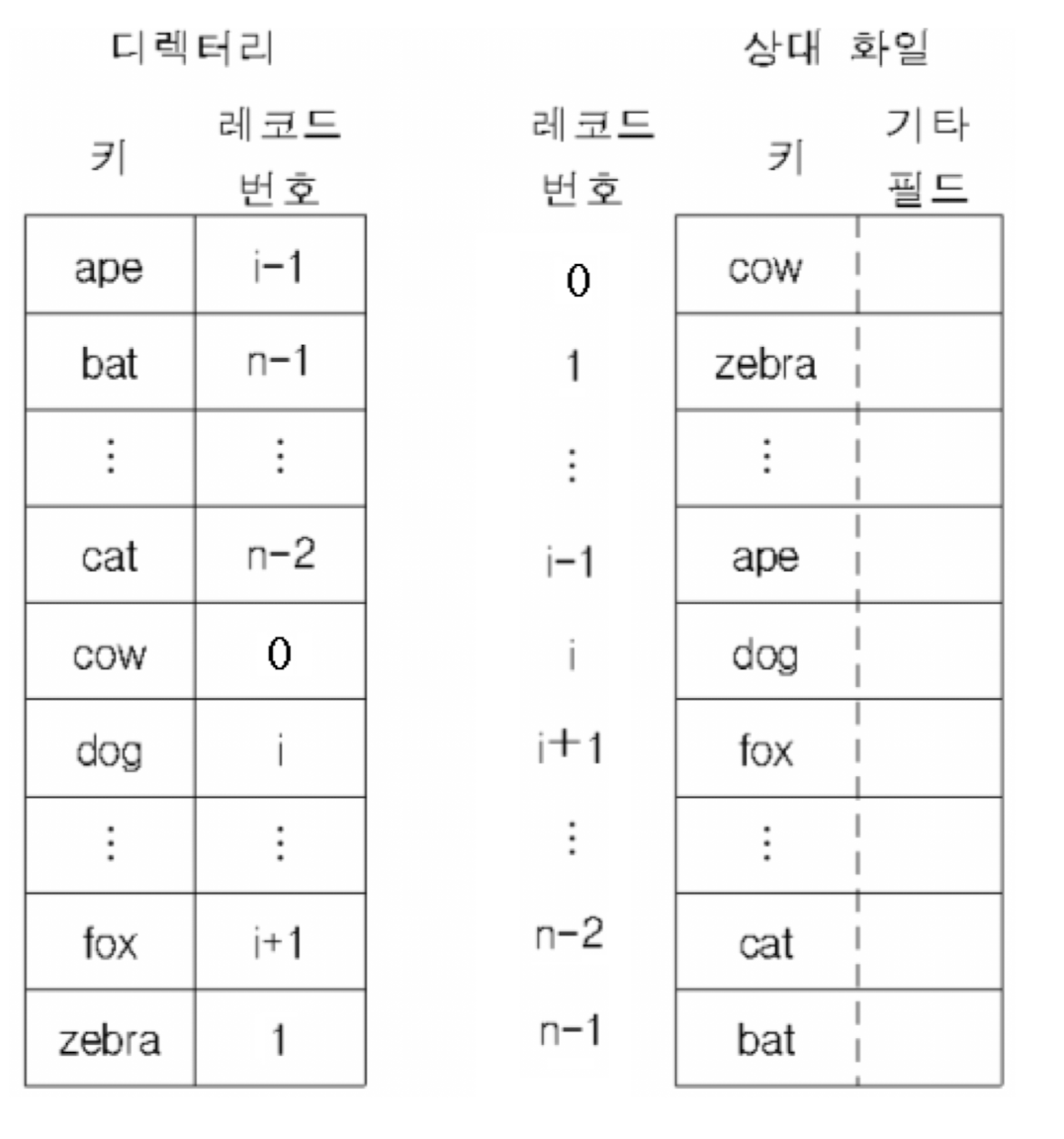
- 상대 화일 접근을 위해 디렉터리 유지
    
    → <키 값, 상대주소> 테이블
    
- 장점
    
    검색 빠름
    
- 단점
    - 삽입 시간 많이 걸림
    - 화일 구조 유지를 위한 화일과 디렉터리 재구성 필요

• 해싱⭐️
  • 계산을 이용한 사상 함수 구현법
  • 일반적으로는 주소공간 > 키 값 공간 → 함수 이용하여 주소공간 ≤ 키값공간
    
  • 키 값을 주소로 변환, 변환된 주소에 레코드 저장
  • 해시 주소 : 해싱 함수가 키 값으로 변환된 주소
  • 해시 화일 : 해싱 기법으로 운영되는 화일
• 해시 화일 설계시 고려 사항

  1. 버킷 크기

     

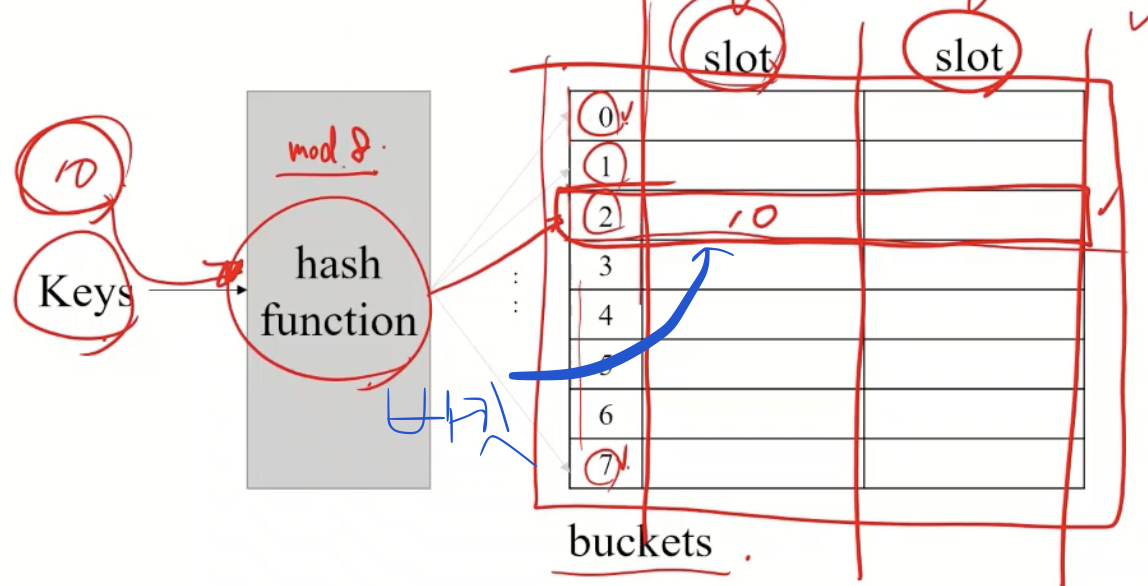
    - 하나의 주소를 가진 저장 구역에 저장할 수 있는 레코드 수
    - 버킷 = 하나의 주소를 가진 저장 구역
    - 같은 버킷 내 모든 레코드는 같은 버킷 주소
    - 하나의 레코드 저장(슬롯)의 집합
    - 버킷 크기 = 버킷에 저장할 수 있는 레코드 수, 물리적 특성과 연관
        
        → slot 개수
        
    - 충돌
        - 상이한 레코드가 똑같은 버킷으로 해싱되는 경우
        - 하나의 버킷에 있는 키 값들 = 동거자(synonyms)
        - 버킷 만원 → 충돌 → 오버플로 발생 → 오버헤드
    - 슬롯 개수 늘리면
        - 오버 플로 발생 확률 감소
        - 저장 공간 효율성 감소 → 탐색 시간 증가
2. 적재율
    - 총 저장 용량에 대해 실제로 저장되는 레코드 수의 비율
    - 적재 밀도 = 저장된 레코드 수 / 버킷크기*버킷수 < 1
        
        = 저장된 레코드 수  / 전체 슬롯 개수
        
    - 높으면
        - 삽입 검색 시 접근 시간 증가
        - 70% 이상이면 충돌 가능성 높음
    - 낮으면
        - 공간 효율 떨어짐
    
    ⇒ 30%의 자유공간 예비하는 것이 바람직
    
    ![](https://velog.velcdn.com/images/jnary/post/0abb936b-d4d3-48b9-bf5f-39702879ed09/image.png)


    
    → mod 7144
    
3. 해싱 함수
    - 레코드 키 값으로부터 주소 생성법
4. 오버플로 해결 방법
    - 주어진 주소 공간이 만원이 된 경우의 해결법

해싱 함수

• 해싱 함수

  • h : 키 → 버킷 주소
  • 해싱 함수 계산 시간 <<<<<<< 디스크의 버킷 접근 시간
  • 모든 주소에 대한 균일한 분포가 굳

• 주소 변환 과정

  • 숫자 X → 정수 값 A로 변환
  • 주소 공간의 자리수 크기의 정수 B로 변환
  • 실제 범위에 맞게 조정 B * 조정 인수 = 주소
    

• 제산 잔여 해싱

  

  • h(key) = key mod d → 0 ~ d-1
    
  • 제수 d → 직접 주소 공간의 크기 결정 (d > 화일의 크기) → 충돌 가능성이 가장 적은 것으로 (20이하의 소수 인수 X)
    
  • 성능
    • 적재율 최대 허용치는 70% ~ 80%

• 중간 제곱 해싱

  

  → 0.5 곱한 게 조정인수

  • 키 값 제곱
  • 중간에서 n개(주소공간)의 수 취함

• 중첩(Folding) 해싱

  

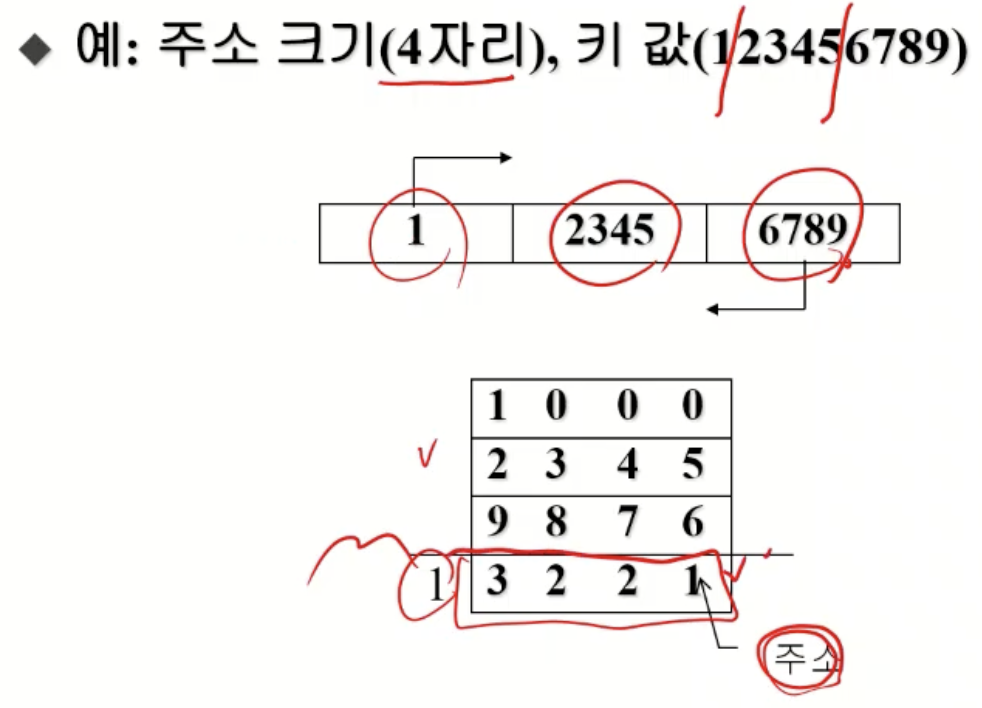
  • 주소의 크기와 같은 자릿수를 갖는 몇 개의 부분으로 나눔
  • 접어서 합 구함

• 숫자 추출 방법

  

  • 키 값이 되는 숫자의 출현 분포 이용
  • 충돌 횟수 줄여 ! 중복 안 돼 !
  • 키 들의 모든 자릿수에 대한 빈도 테이블 생성

• 숫자 이동 변환

  

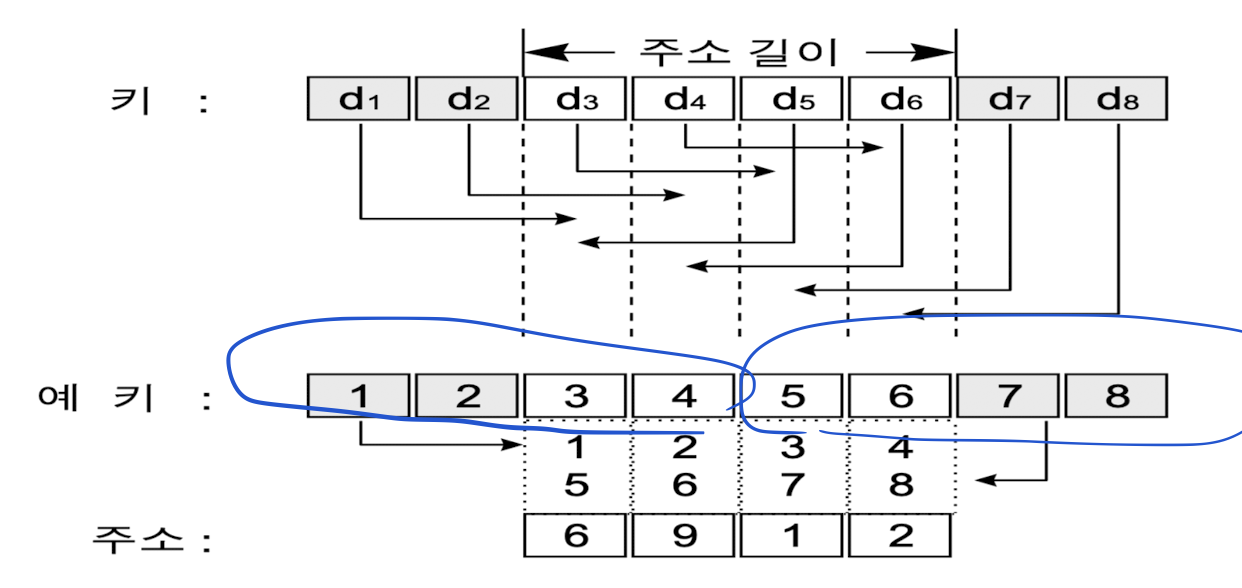
  • 키를 중앙(N/2개)을 중심으로 양분
  • 주소 길이만큼 겹치도록 안쪽으로 shift하여 합산
  • 주소 범위에 맞도록 조정 ← 조정 인수(0.5)

• 진수 변환

  

  • 키 값의 진수를 다른 진수로 변환
  • 초과하는 높은 자리수 절단
  • 주소 범위 맞도록 조정 ← 조정 인수

충돌과 오버플로

• 키 값 공간 > 주소 공간 → 충돌 발생 불가피
• 오버플로
  • 홈 주소(홈버킷)으로 충돌된 동거자들을 한 버킷에 모두 저장할 수 없는 경우 → 홈 주소 : 해싱 함수가 생성한 버킷 주소
    
  • 해결 방법
    1. 선형 조사
    2. 독립 오버플로 구역
    3. 이중 해싱
    4. 동거자 체인
    5. 버킷 체인

←————버킷 크기(버킷 하나당 슬롯 개수) 1로 가정 ———————>

• 선형 조사

  

  • 홈 주소에서부터 차례로 조사 → 가장 가까운 빈 공간 찾기
  • 해당 주소가 공백인 지 여부 flag에 저장
  • 저장 : 원형 탐색 → 다시 화일 시작으로 돌아가 홈 주소에 도착할 때 종료
  • 검색 : 선형 조사 방법 사용 필수
  • 삭제 : 삭제로 생긴 빈공간 검색 → 선형 조사 단절될 수도 → 삭제 표시 (tombstone) 필요
    
  • 단점
    • 화일에 없다는 것 판단하기 위해 조사해야할 주소의 수가 많아짐 → 적재율이 높아질 수록 많아짐 (적당한 적재율 유지 필요)
      
    • 환치

      • 동거자가 아닌 다른 오버플로된 레코드 때문에 다른 레코드의 홈주소에 저장되는 것

      • 연쇄 작용

        → 2-패스 해시 화일 생성으로 해결

  • 2-패스 해시 화일 생성

    1. 첫 번째 패스

       • 해시 함수를 통해 홈 주소에 저장
       • 오버플로된 동거자 → 별도 임시 화일에 저장

    2. 두 번째 패스
       - 임시 화일에 저장해둔 오버플로 동거자들 선형 조사로 적재

       → 환치 방지

---

• 독립 오버플로 구역

  

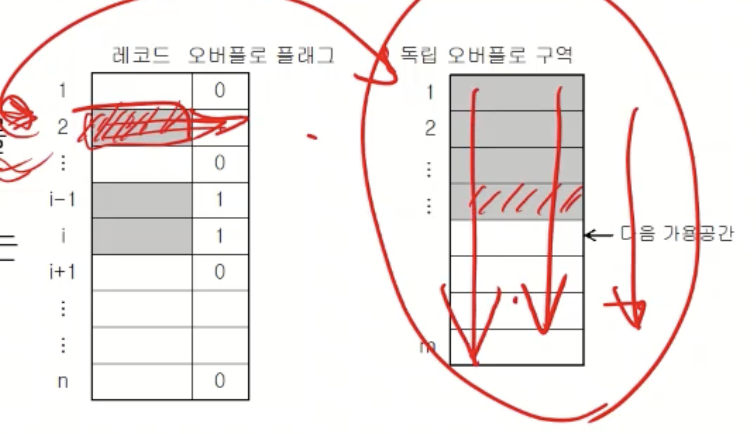
  • 별개의 오버플로 구역 할당 → 모든 동거자들 순차 저장
  • 장점
    • 환치 문제 발생 X
    • 1-패스로 상대 화일 생성
    • 동거자아닌 레코드는 한 번의 홈 주소 접근 만으로 레코드 검색 가능
  • 단점
    • 오버플로된 동거자 접근 → 순차 검색 필요 (낮은 검색 효율)

---

• 이중 해싱
  • 2차 해싱 함수 : 오버플로된 동거자 해시
  • 1차 해싱 함수에 의해 상대 화일로 해시
  • 오버플로 발생시 오버플로 구역으로 해시 (1차 해시 주소 + 2차 해시 주소) mod (오버플로 구역 크기)
    
  • 오버플로 재차 → 선형 탐색 이용

---

• 동거자 체인

  

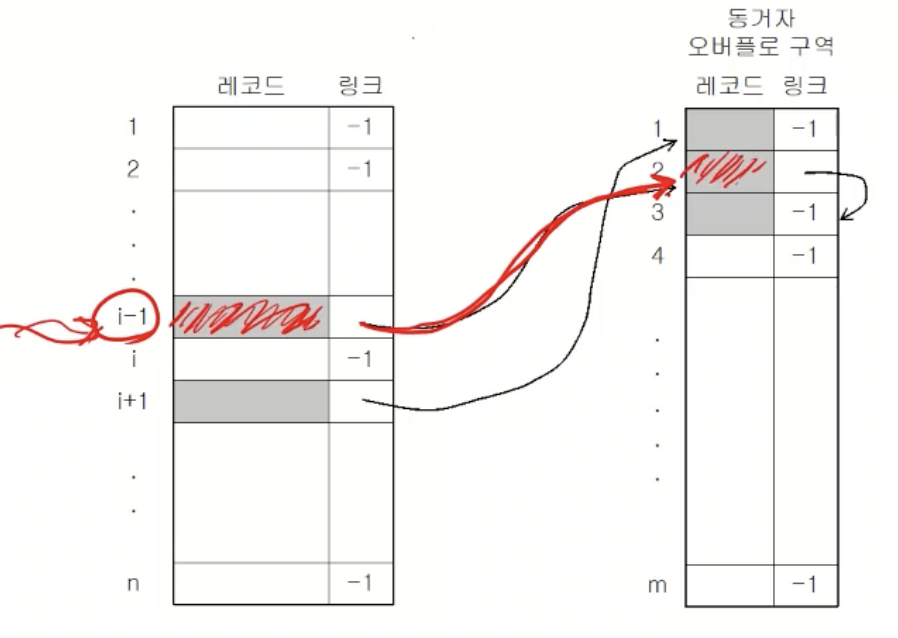
  • 각 주소마다 링크를 두어 오버플로된 동거자 레코드들을 연결
  • 독립 오버플로 구역, 원래 상대 화일에서 사용 가능
  • 장점
    • 홈 주소에서의 충돌 감소
    • 환치 문제 X
  • 단점
    • 각 주소가 링크 필드를 포함할 수 있도록 확장 필요

---

• 버킷 체인
  • 동거자 체인과 비슷
  • 동거자 오버플로 발생 → 별개의 버킷 할당, 오버플로된 동거자 저장 → 홈 버킷에 이 버킷을 링크로 연결
    
  • 다른 방법보다 평균 조사 수 적음
  • 장점
    • 재해싱 불필요
    • 독립 오버플로 구역 사용시 환치 문제 X
  • 단점
    • 확장 필요
    • 홈 버킷에 연결된 모든 오버플로 버킷 조사 필요

테이블 이용 해시 화일

• 저장장치에 한 번의 접근으로 레코드 검색 보장

  • 삽입시간 많이 걸림
  • 검색 매우 빠름 → ex. 로그인 확인할 때 자주 접근(내용 드물게 변경)
    
  • k-비트 시그너쳐(Sign) 생성 기법 필요
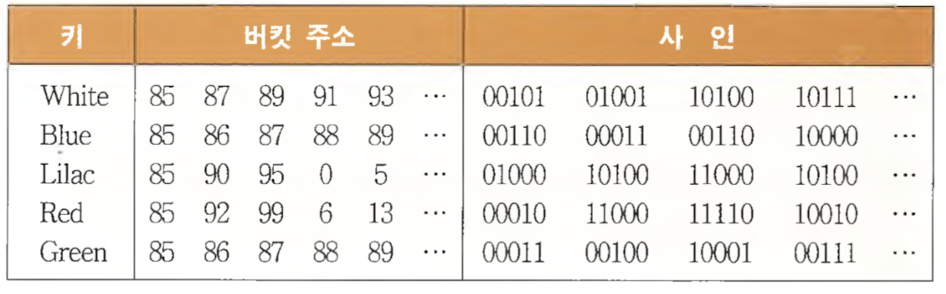
  • 해싱함수 : <버킷 주소, k-비트 시그너쳐> 쌍 생성
  • 각 버킷에는 하나의 엔트리(k-비트 시그너쳐)된 버킷 테이블 유지
  • 화일 접근 시 버킷 테이블 → 메인메모리에 상주 → 탐색 한 번에 가능
    

• 테이블 이용 해싱 (버킷 크기 = 3이라 가정)

  • White, Blue, Lilac 삽입 → 만원
  • Red 삽입 오버플로 → 버킷에 대한 각 레코드의 시그너처 값에 따라 정렬
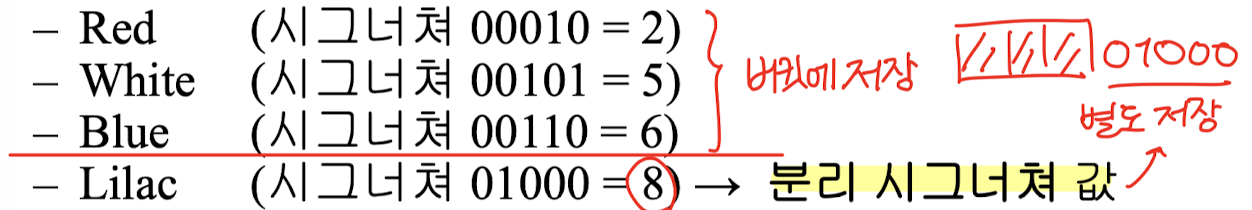
  • 분리 시그너쳐 값

    • 버킷 85에 대한 버킷 테이블 엔트리로 저장

    • 버킷에는 항상 분리 시그너쳐 값보다 작은 레코드만 저장

      → Lilac 두번째 버킷 주소 90에 따로 저장

  • 버킷 테이블 엔트리(시그너쳐 값) : 초기치11111에서 오버플로되는 경우에만 갱신
    • Red, White, Blue : 버킷 85에 저장 → 테이블 엔트리는 01000
    • Lilac : 버킷 90에 저장 → 테이블 엔트리는 11111
  • Green 삽입
    • 홈 버킷 85의 시그너쳐 = 01000 > Green의 시그너쳐 00011
    • 시그너쳐 정렬
    • Green 삽입, Blue 오버플로
    • 테이블 엔트리 Blue 시그너쳐 00110으로 갱신
    • Blue 두 번쨰 버킷 주소 86에 따로 저장

확장성 직접 화일

• 확장성 직접 화일
  • 화일 레코드 수의 변화가 큰 경우에 대한 해결 방안
  • K : 어느 한 시점에서 화일에 저장된 레코드 수
    • Kmin ≤ K ≤ Kmax
    • SPAN = Kmax/Kmin ← 크면 문제 발생
    • 화일 크기 고정되어 있을 경우 Kmin : 낮은 공간 이용률 Kmax : 높은 적재 밀도 → 저장과 검색 시간 증가
      
  • 해결책 : 재해싱

    • 많은 시간 소요, 재해싱 동안 접근 제한

      → 해결책 : 확장성 직접 화일

  • 높은 SPAN값을 가지는 화일 조직에 대한 해싱 기법
  • 버킷 크기 일정 , 버킷 수 가변
  • 오버플로 버킷 사용 X (고정된 상태 X)
  • 삭제 간단, 검색은 1-2회의 접근만
  • 유형
    1. 가상 해싱
    2. 동적 해싱
    3. 확장성 해싱
    4. 선형 해싱

---

• 가상 해싱

  

  • 여러 개의 해싱 함수 사용
  • 해싱 함수 = 제산 잔여 기법 기초 (주소 = 키 mod N)
  • 오버플로우
    • 기존 레코드와 삽입하려는 레코드 모두 재해싱
    • 재 해싱 함수 hi = 키 mod (2^i * N)

---

• 동적 해싱

  

  • 크기가 C인 N개의 버킷 + 버킷을 지시하는 인덱스

    • 버킷 : 저장장치에
    • 인덱스 : 메인 메모리에

  • 삽입

    

    

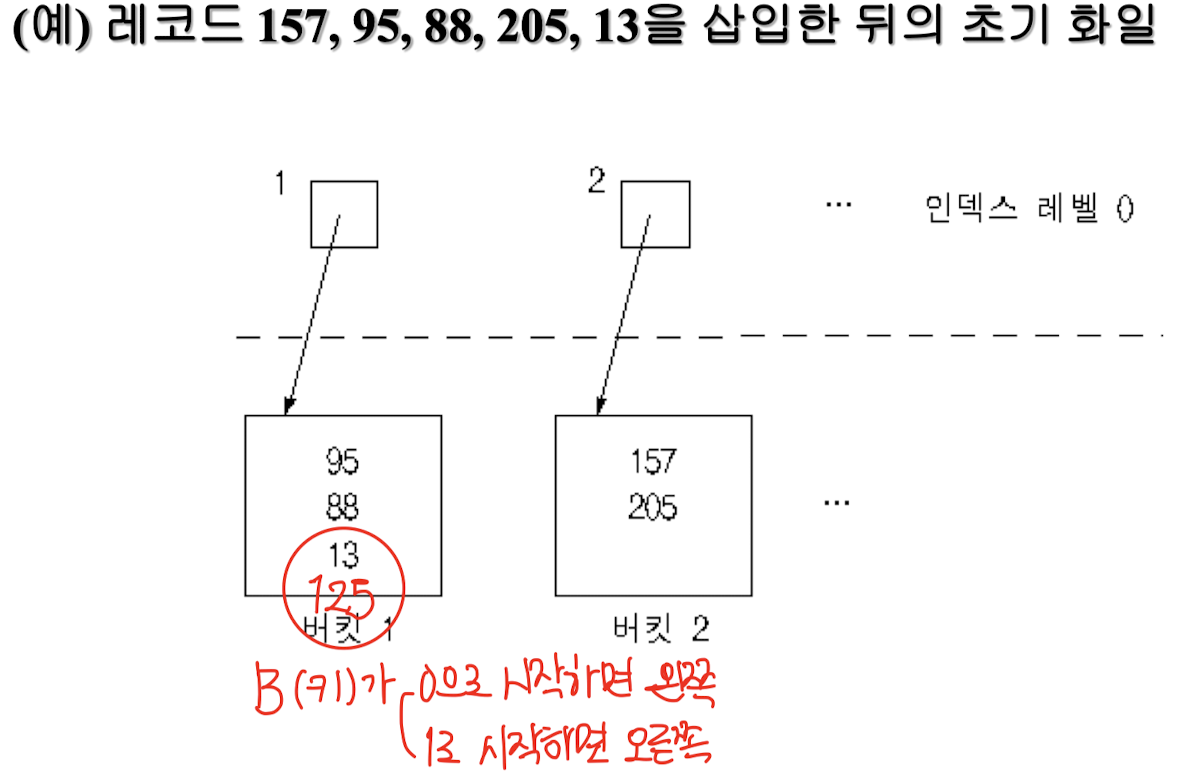
    • 해싱 함수 : 키 값 → 레벨 0 인덱스 엔트리의 주소
    • 오버플로
      • 새로운 버킷 생성
      • 만원 되었던 버킷, 새로 할당된 버킷에 분할 저장
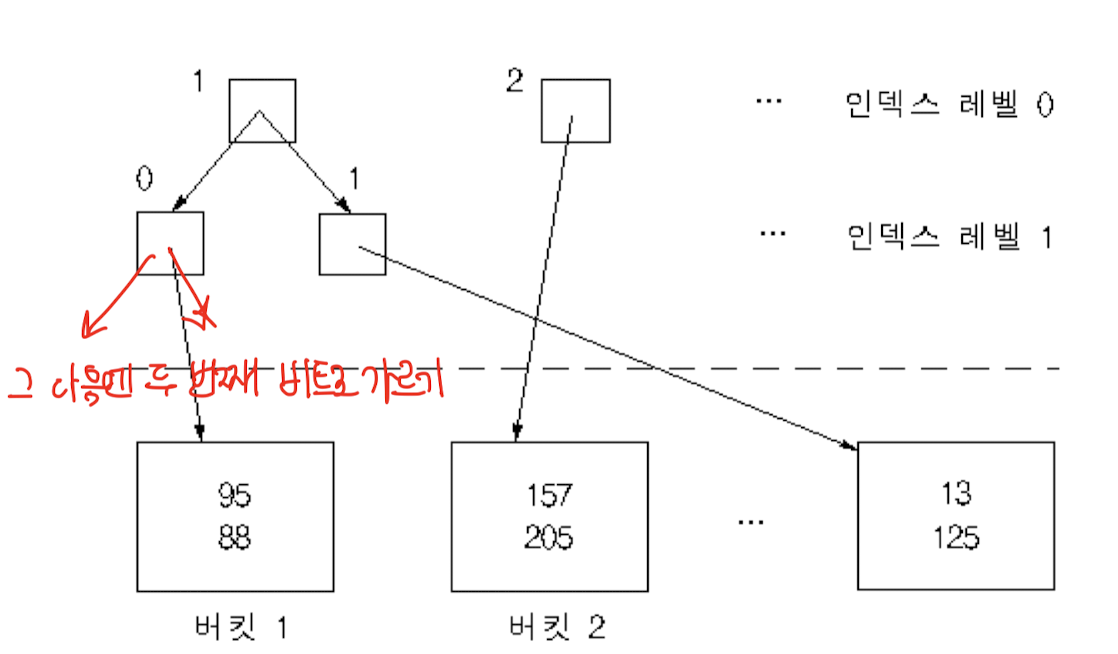
      • 인덱스 노드 : 두 포인터를 갖는 이진 트리의 내부 노드로 전환
      • 이진 트리 집합 : 포레스트
    • 내부 노드 : 0, 부모 포인터, 왼쪽 자식 포인터, 오른쪽 자식 포인터
    • 외부 노드 : 1, 부모 포인터, 저장된 레코드 수, 버킷 포인터

  • 버킷 분할

    

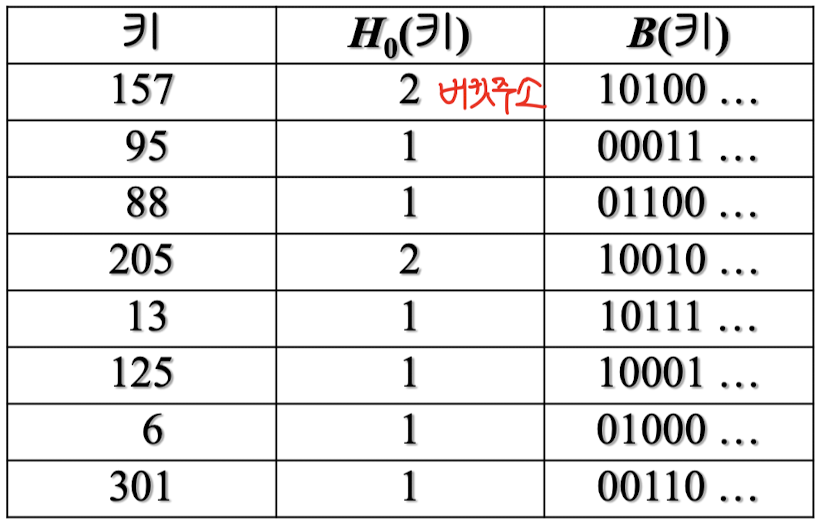
    • 분산 저장해야 될 레코드의 버킷이 왼쪽인지 오른쪽인지 결정
    • 비트 함수 B : 키 값을 임의의 길이의 비트 스트링으로 변환
    • 인덱스가 분기되는 레벨 i, 비트스트링 i+1번째 비트가 → 0이면 왼쪽 → 1이면 오른쪽
      
    • 설계 : 모조난수 생성기의 초기 값 사용 → 생성된 각 정수를 하나의 비트로 변환 (0과 1이 똑같은 확률로 생성될 수 있도록 변환)
      

  • 검색

    • 해싱함수 H0로 인덱스 레벨 0의 포레스트 식별
    • 레코드 키 값에 대한 함수 B의 비트 스트링 값으로 인덱스 레벨1부터 분기하여 검색할 버킷 결정

---

• 확장성 해싱

  

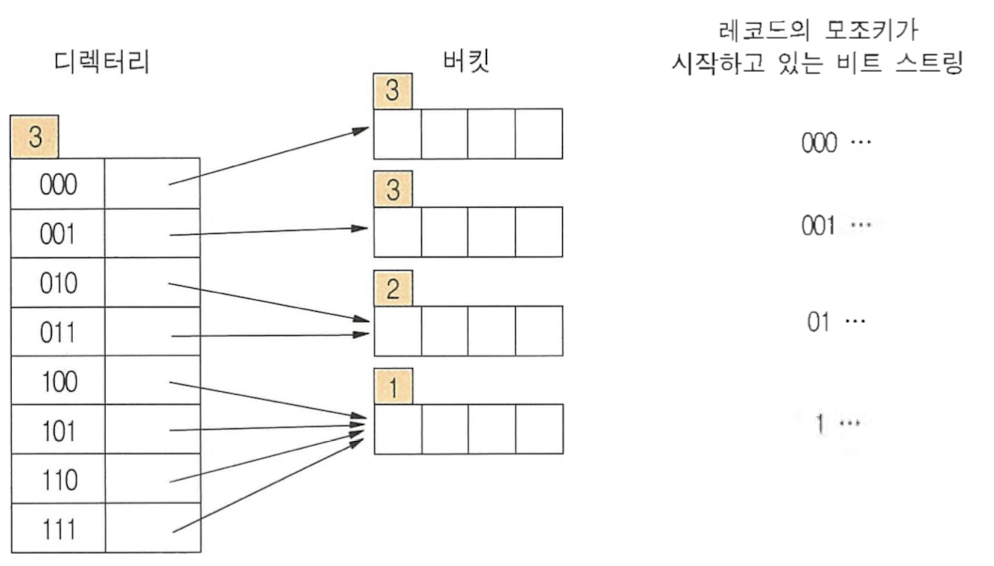
  • 확장성 해싱 함수 : 키 값 → 일정 길이의 비트 스트링(모조키)로 변환
  • 디렉터리 + 버킷
    1. 디렉터리
       • 일반적인 인덱스
       • 버킷에 대한 2^d개의 포인터로 구성 → 같은 버킷 가리킬 수 있음
         
       • d = 전역 깊이 (디렉터리 크기) N개 버킷 시작 → d = log(N-1) + 1
         
    2. 버킷
       • 레코드들을 실제로 저장하는 공간
       • 각 버킷은 지역 깊이(p) 표시 → 버킷에 저장된 모든 레코드들의 모조키들이 첫 번째 비트부터 공통으로 가지고 있는 비트 스트링 길이
         
  • 검색
    • d=3 → 모조키의 처음 3비트를 이용해 디렉터리의 엔트리 접근
    • 엔트리는 버킷에 대한 포인터
    • p값 1은 저장된 레코드들의 공통 모조키 비트 수가 1이라는 것
  • 저장 시 오버플로
    • 새로운 버킷 할당
    • 모조키의 p +1번째 비트에 따라 두 버킷에 분산 저장
    • 기존 버킷과 새로 할당한 버킷의 깊이 p를 모두 p +1로 설정

      1. d ≥ p + 1 이면

         디렉터리의 해당 포인터 엔트리만 조정

      2. d < p + 1 이면

         디렉터리 깊이 d 값 ++

         디렉터리 크기 2배로 확장한 다음 포인터 엔트리 조정

  • 삭제
    • 검색 과정으로 찾아 삭제
    • 삭제 후 빈 버킷이 되는 경우
      • 버티 버킷 : 두 버킷이 똑같은 버킷 깊이(p) + 레코드 모조키들의 처음 p-1비트들이 모두 동일
      • 버디 버킷 검사 → 한 버킷에 들어갈 수 있으면 합병 → 새로운 깊이 값은 p-1
        
      • 모든 버킷들의 깊이 값이 디렉터리 값보다 작아지면 d— → 크기 절반 감소 → 포인터 엔트리들 재조정
        

---

• 선형 해싱

  • 디렉터리 사용하지 않는 확장성 해싱 방식

  • 주소 공간 확장 → 해시 값의 비트 사용

    ex. 버킷 주소 공간 = 4 → 2-비트 주소 생성하는 2-비트 해싱 함수 시용
    

  • 오버플로 → 항상 선형으로 확장(사이클 식)

  • 저장

    

    

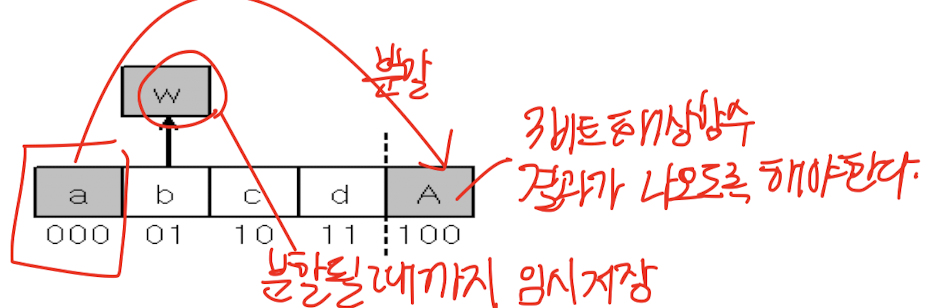
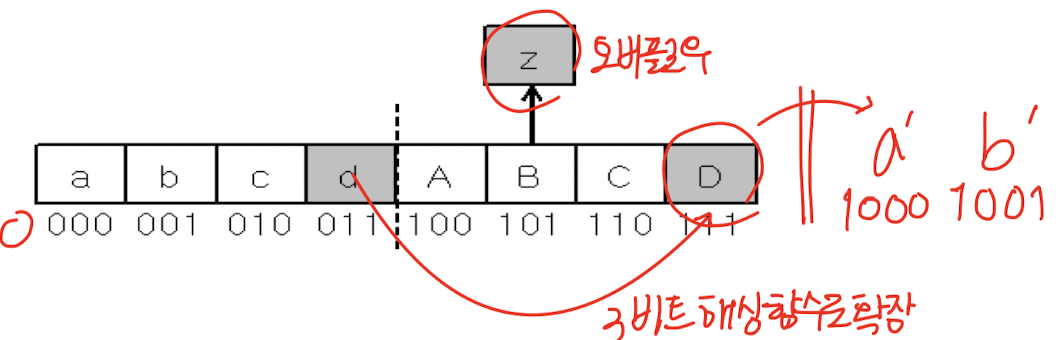
    • 모든 버킷이 3-비트 해싱 함수 사용 → 첫번째 버킷 a를 가리키도록 설정
      
    • 새로운 버킷 생성하여 확장 시에는 4-비트 해싱 함수 사용

  • 검색

    • 두 개의 해싱 함수를 이용해 접근

    • d-비트의 기본 주소를 가진 버킷 : d-비트 해싱 함수 이용

    • 확장 버킷 : (d+1)-비트 해싱 함수 이용

    • 키 값 k를 가진 레코드를 포함하고 있는 버킷 주소 찾기

      

      p = 다음에 분할할 버킷을 가리키는 포인터