일상생활을 하거나 게임을 할때 가끔가다가 '스택을 쌓는다.' 또는 '스택이 쌓였다.'라는 말을 하거나 듣는 경우가 종종 있다.
이 '스택'이라는 것은 무엇으로부터 나왔으며 정확한 개념이 무엇인지 알아보겠다.
스택이란?
스택(stack)은 가장 간단한 형태의 자료구조 중하나로, 후입선출(LIFO: Last In First Out)의 형태로 일어난다. 스택은 가장 먼저 입력된 데이터가 맨 아래로 쌓이고 가장 최근에 입력된 데이터가 가장 위에 쌓이는 구조를 가지고 있다. 스택에서의 입출력은 맨 위에서만 일어나고 스택의 중간에서는 데이터를 삽입하거나 삭제할 수 없다.
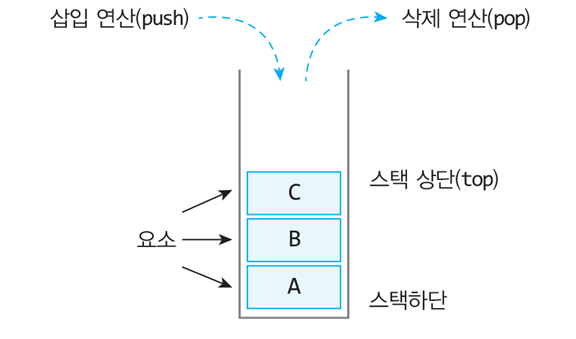
- 요소(element): 스택에 저장되는 것
- 공백(empty)상태: 스택에 요소가 하나도 없는 경우
- 포화(full)상태: 스택이 꽉 차서 더 이상 요소를 넣을 수 없는 상태
※ 주의 : element가 1이면 top은 0이고, element가 0 이면 top은 -1
→ 배열은 0 부터 시작하기 때문
스택의 추상 자료형
| 객체 | 후입선출(LIFO)의 접근 방법을 유지하는 요소들의 모음 |
|---|---|
| 연산 | push(): 주어진 요소 x를 스택의 맨 위에 추가한다. |
| pop(): 스택이 비어있지 않으면 맨 위에 있는 요소를 삭제하고 반환한다. | |
| isEmpty(): 스택이 비어있으면 true, 아니면 false를 반환한다. | |
| peek(): 스택이 비어 있지 않으면 맨 위에 있는 요소를 삭제하지 않고 반환한다. | |
| isFull(): 스택이 가득 차 있으면 true, 아니면 false를 반환한다. | |
| size(): 스택 내의 모든 요소의 개수를 반환한다. | |
| display(): 스택 내의 모든 요소들을 출력한다. |
스택에서 가장 중요한 연산은 요소를 삽입하는 push와 pop이다.
다음 그림은 초기 공백 스택에 일련의 push와 pop 연산이 진행되는 과정을 보여준다.
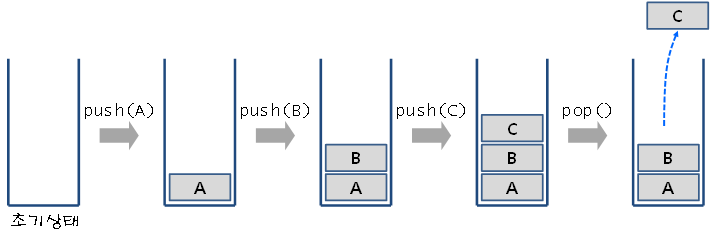
※ peek연산은 요소를 스택에서 삭제하지 않고 보기만 하는 연산이다. 이에 비해 pop 연산은 스택에서 꺼내오기 때문에 스택에서 요소가 없어진다.
스택의 구현
배열은 거의 모든 프로그래밍 언어에서 지원한다. 배열은 순차적인 메모리 공간에 할당된다고 해서 순차적 표현(sequential represention)이라고도 한다. 배열은 같은 자료형의 변수를 여러 개 만드는 경우에 특히 유용하고, 항목을 저장할 수 있는 여러 개의 공간을 제공한다. 각 공간은 정확히 하나의 항목만을 담으며 각 항목들은 인데스 번호를 통해 직접접근할 수 있다. 크기가 고정된 배열은 그 크기만큼의 상자들의 집합과 같다. 상자에는 우리가 저장하고 싶은 항목을 저장할 수 있고, 번호가 붙어 있으며 0 부터 시작한다. 다음은 C++ 배열로 구현한 int 스택 클래스이다.
#pragma once
#include <stdio.h>
#include <stdlib.h>
#define MAX_STACK_SIZE 100
inline void error( char* str ) {
fprintf(stderr, "%s\n", str);
exit(1);
};
class ArrayStack
{
int data[MAX_STACK_SIZE]; // 요소의 배열
int top; // 요소의 개수
public:
ArrayStack() { top = -1; } // 스택 생성자
~ArrayStack(){} // 스택 소멸자
bool isEmpty() { return top == -1; }
bool isFull() { return top == MAX_STACK_SIZE-1; }
void push ( int e ) { // 맨 위에 항목 삽입
if( isFull() ) error ("스택 포화 에러");
data[++top] = e;
}
int pop ( ) { // 맨 위의 요소를 삭제하고 반환
if( isEmpty() ) error ("스택 공백 에러");
return data[top--];
}
int peek ( ){ // 맨 위의 요소를 삭제하지 않고 반환
if( isEmpty() ) error ("스택 공백 에러");
return data[top];
}
void display ( ) { // 스택 내용을 화면에 출력
printf("[스택 항목의 수 = %2d] ==> ", top+1) ;
for (int i=0 ; i<=top ; i++ )
printf("<%2d>", data[i]);
printf("\n");
}
};연결 리스트를 이용한 스택
배열을 이용하여 구현한 스택은 구현이 간편하지만 스택의 크기가 제한 된다는 약점이 하나 있다.(동적으로 생성이 불가능하다.)
이 약점을 보완하기 위해서는 연결 리스트를 이용해야 한다.
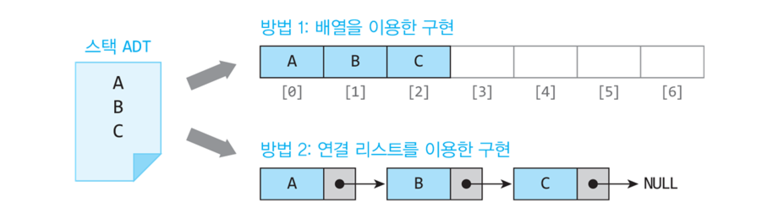
연결리스트를 설명하자면 게시글이 너무 길어지기 때문에 나중에 따로 연결리스트에 대해 투고하려한다. 연결리스트를 간단히 설명하자면 복잡한 포인터 연산을 필요로 하는 구현 방법이다.
