0. 서론
지난 시간에는 deep learning의 기본인 linear regression에 대해 배웠다. 그러나 실제로 deep learning 모델이 단순한 linear regression으로 이루어지지 않을 것이다. 당장 chatGPT가 그렇게 나온다고 상상해보자 그렇다면 실제 deep learning model은 어떻게 되었을까? 우리 함께 MLP의 세계 속으로 빠져들어보자.
1. MLP(Multi Layer Perceptron) 이란?
1) 대략적인 설명
사실 개미 한 마리의 행동은 그렇게 복잡하지 않다. 먹이가 있으면 찾으러 가고, 날 잡아먹으려는 게 있으면 피하고, 짝이 있으면 찾고... 매우 단순하다. 그러나 개미 천 마리에서 만 마리 정도가 모이니까 어떤 일을 하는가? 놀랍게도 그들은 하나의 세계를 만들고 사회를 만든다.
이처럼 단순한 linear regression도 "여러 번 쌓아 올리면 복잡한 작업이 가능하지 않을까?"라는 행복회로에서 나온 아이디어가 MLP라고 할 수 있다. 잘 생각해 보면, 우리의 뇌 역시 단순한 뉴런의 연결을 수억~수조 개 쌓아올려서 이루어졌음을 생각하면 충분히 할 수 있는 킹리적 갓심이다.
2) Activation function과 그 필요성
그러나 사실 위에서 보여준 수식은 하나의 어패가 있다. 사실 저건 linear regression과 크게 다를 것이 없다(...)
저 수식을 정리하면 다음과 같을 것이다. 그런데, 이 W는 하나의 input size* output size 행렬로, 저런 개 노가다를 뛰느니 차라리 그냥 해서 깔끔하게 처리해 버리는 것이 낫다. 그렇다면 어떻게 해야 할까?
이렇게 중간에 어떤 함수를 만들어버리면, 이런 문제를 해결할 수 있다. 우리 뇌도 비슷하게 작동하지 않는가. 뉴런에 정보가 전달되면 시냅스에서 그걸 받아들일지 말지 처리한다. 딥 러닝 모델도 이와 같다고 할 수 있다. 여기 있는 f(x)를 activation function이라고 한다. 다음 행렬 연산으로 덤어갈 데이터를 0이나 작은 값으로 처리할지, 아니면 그대로 전하거나 큰 값으로 전해줄지 결정해주는 역할을, activation function이 맡아준다고 보면 된다.
3) activation function의 종류
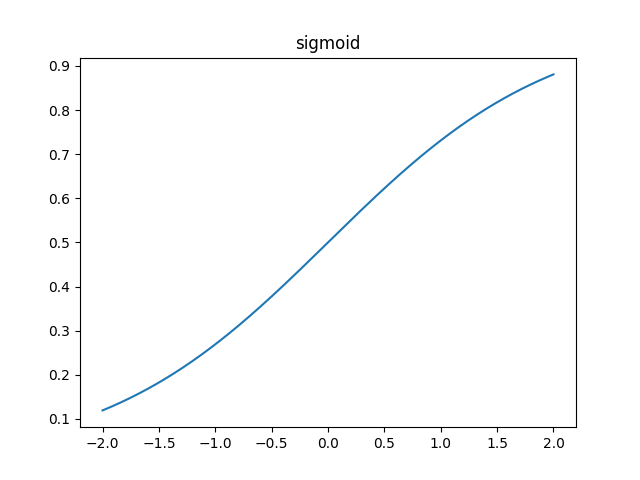
1) sigmoid
양으로는 1에 무한히 수렴하고 음으로는 0으로 무한히 수렴한다. 어찌 보면 우리가 직관적으로 생각하는 시냅스의 모습을 잘 담았다고 볼 수 있다.
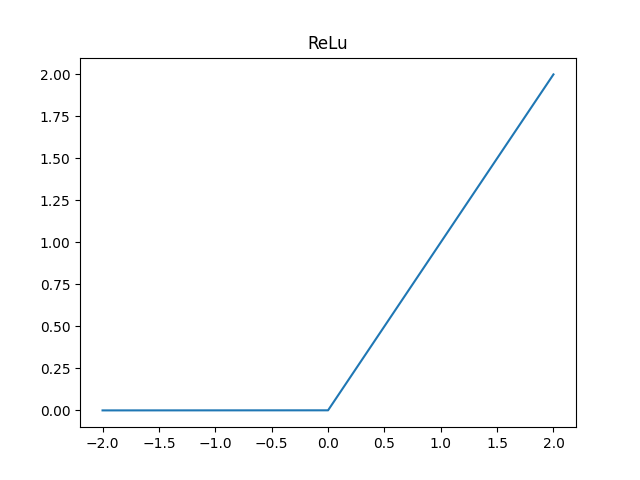
2) ReLu
현재 가장 많이 쓰이는 친구로, Reaky ReLu와 같은 variation들이 상당히 많다. 너무 단순하게 생겼으니 자세한 내용은 생략한다.
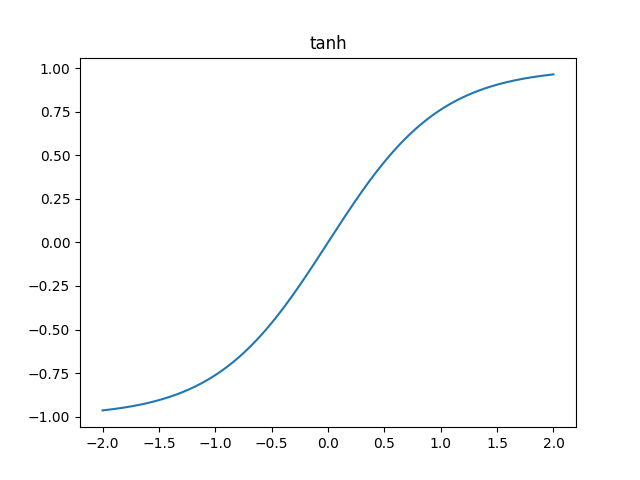
3) tanh
말 그대로 hyperbolic tangent다. 모르는 고등학생 친구를 위해 설명해주자면, 대충 이런 함수다. 양으로는 1에 무한히 수렴하고 음으로는 -1로 무한히 수렴한다.
그 외에도 여러 바리에이션이 있으나 대표적으로 저 세 개만 알아도 충분하다. 보다시피 절대 직선이면 안 되고 곡선이거나 미분 불가능해야 한다. activation function의 목적은 선형 연산을 깨부수는 거기 때문이다.
4) MLP의 실행
그렇다면 위에서 하던 image classification 작업이 떠오르는가? 그걸 실제로 실행할 수 있는 MLP를 디자인해 보자.
from torch import nn
import torch.nn.functional as F
class MLP(nn.Module):
def __init__(self):
super.__init__()
pass
def forward(self, x):
pass다음과 같이, 모델 클라스를 만들 때에는 데이터셋을 만들 때처럼 torch.nn.Module을 상속받는 것이 국룰이다. x는 당연히, input으로 들어가는 데이터나 batch가 될 것이다.
그러면 여기서 반드시 오버라이딩되어야 하는 함수는 __init__과 forward다. 이제 __init__과 forward에 무엇을 넣어야 할지 보도록 하자.
from torch import nn
import torch.nn.functional as F
class MLP(nn.Module):
def __init__(self):
super.__init__()
self.layer1 = nn.Linear(1024*3, 2048)
self.layer2 = nn.Linear(2048, 2048)
self.layer3 = nn.Linear(2048, 10)
self.activation = nn.ReLU
def forward(self, x):
hidden1 = self.layer1(x)
hidden1 = self.activation(hidden1)
hidden2 = self.layer2(hidden1)
hidden2 = self.activation(hidden2)
hidden3 = self.layer3(hidden2)
output = self.activation(hidden3)
return output이와 같이 __init__에서는 사용할 layer들을 선언하고, forward에서는 그 layer들을 input x가 들어올 때 선언된 layer들을 사용하면 된다.
여기서는 nn.Linaer을 사용했는데, 이건 그냥 y=Wx를 출력하는 행렬 연산 레이어다. nn.Linaer(input, output)에서 input은 input layer의 길이, output은 output layer의 길이가 된다. 즉, input에 들어가야 하는 layer의 크기는 (1024*3, batch_size)인 셈이다. 근데 여기서 input layer의 길이를 쓰기 귀찮으면...
from torch import nn
import torch.nn.functional as F
class MLP(nn.Module):
def __init__(self):
super.__init__()
self.layer1 = nn.LazyLinear(2048)
self.layer2 = nn.Linear(2048, 2048)
self.layer3 = nn.Linear(2048, 10)
self.activation = nn.ReLU
def forward(self, x):
hidden1 = self.layer1(x)
hidden1 = self.activation(hidden1)
hidden2 = self.layer2(hidden1)
hidden2 = self.activation(hidden2)
hidden3 = self.layer3(hidden2)
output = self.activation(hidden3)
return output그냥 nn.Linear대신 nn.LazyLinear을 쓰면 된다.
if __name__ == "__main__":
x1 = torch.randn(4, 1024*3)
x2 = torch.randn(16, 1024*3)
x3 = torch.randn(64, 1024*3)
model = MLP()
print(model(x1).size())
print(model(x2).size())
print(model(x3).size())
이렇게 시험을 해보면,
❯ python3 MLPNet.py
torch.Size([4, 10])
torch.Size([16, 10])
torch.Size([64, 10])
(.env)output이 다음과 같이 아름답게 나온다. 이처럼 다양한 batch size에도 적용이 됨을 알 수 있다. 끗!