딥러닝 유치원2 - 딥러닝의 기본 중의 기본, Linear Regression

조영유·2025년 4월 2일

deeplearning-kindergarten

목록 보기

2/5

1. 서론

다시 상술한 예시로 돌아가자. 만일 당신이 열역학을 마스터하고 싶다고 하자. 그러면 당신은 다음과 같은 과정을 밟을 것이다.
1) 문제집을 푼다. 챕터별로 16문제 정도 있으면 16문제 푼다.
2) 채점을 한다.
3) 틀린 내용을 고치고 부족한 부분을 공부한다.
4) 문제집을 푼다. 어제의 나보다 나는 발전해 있을 것이다.
5) 다시 채점을 하고 틀린 내용을 보강한다.
... 무한반복 ...
6) 시험을 친다. 내가 어느 정도로 공부를 잘하는지 확인한다.
1) 다시 문제집을 푼다.

놀랍게도 딥 러닝 모델도 정확히 같은 방식으로(!) 모르는 내용을 공부한다. 이걸 적용해서 딥 러닝 모델이 어떻게 트레이닝하는지 알아보자.
1) 주어진 input $x$ 에 대하여 결괏값 $y=f(x)$ 를 도출한다.
2) $y$ 가 정답 라벨 $\hat{y}$ 에 얼마나 가까운지 그 정확도를 측정한다. 문제집처럼 한 16개 정도 넣고 계산한다 해 볼까?
3) 정확도를 높이기 위한 f(x)의 변수들을 보정한다.
4) 다시 주어진 input $x$ 에 대하여 결괏값 $y=f(x)$ 를 도출한다.
5) 정확도를 다시 측정하고 보정한다.
...무한반복...
6) 주어진 input $x$ 에 대하여 결괏값 $y=f(x)$ 를 도출하고, 그 정확도를 측정한다. 여기서는 시험이기 때문에 변수를 보정하지 않는다. 솔직히 수능 보고 오답노트 쓰는 미친 놈이 세상에 어디 있는가?
1) 다시 training을 한다.

눈치가 빠르면 알 것이다. 1에서 5까지의 x는 train set에서 나오는 값이며, 6번에서의 x는 test set에서 나오는 값이다. 이렇게 1부터 6까지 거쳐가는 과정을 한 epoch 이라고 한다. 그러면 이 과정은 어떻게 이루어질까? 그 과정을 수학적으로, 정확히 짚고 넘어가는 것이 우리의 의무일 것이다.

2. 딥러닝의 기본 중 기본 - Linear regression

1) 이론

만약에 당신이 돈을 많이 벌고 싶다고 하자. 그래서 주위 사람들 한 1000명 정도에게 물어봐서 돈을 많이 번 사람들이 전부 근면함, 운, 사회성, 정리 능력 등 어떤 역량을 가졌는지 물어보고 그걸 수치화했다고 치자. 예를 들어서, 만약 철수가 1번이면, 철수의 역량은 다음과 같이 정리될 것이다.

\vec{x_{1}}=(x_{work hour}, x_{luck}, x_{social ability}, x_{organization})

이 때 그들의 연봉, 보너스, 인망을 계산한다 해 보자.

\vec{y_{1}}=(y_{salary}, y_{bonus}, y_{honour})

여기서 이 값을 계산하는 가장 단순한 방법은 다음과 같이 각 요소에 얼마나 가중치가 들어가는지 고려하는 선형적 방법일 것이다.

y_{salary}=w_{11}x_{work hour}+ w_{12}x_{luck}+ w_{13}x_{social ability}+w_{14}x_{organization} + b_{salary}

y_{bonus}=w_{21}x_{work hour}+ w_{22}x_{luck}+ w_{23}x_{social ability}+w_{24}x_{organization} + b_{bonus}

y_{honour}=w_{31}x_{work hour}+ w_{32}x_{luck}+ w_{33}x_{social ability}+w_{34}x_{organization} + b_{honour}

이를 행렬로 만들면 다음과 같이 표현될 것이다. 당연히 여기에 있는 W에 있는 값들은 weights라고 불린다.

\vec{y_{i}}=\vec{x_{i}}W + \vec{b}, W= \begin{Bmatrix} w_{11} & w_{21} & w_{31} \\ w_{12} & w_{22} & w_{32} \\ w_{13} & w_{23} & w_{33} \\ w_{14} & w_{24} & w_{34} \\ \end{Bmatrix}, \vec{b}= (b_{salary}, b_{bonus}, b_{honour})

그렇지만 컴퓨터 입장에서, 아니 사람도, 한 문제만 풀고 채점하는 건 좀 그렇다. 그렇기 때문에 여러 문제를 풀고 체점하게 해야 할 것이다. 특히나 행렬 연산에 특화된 GPU의 경우 더욱 그렇다. 이렇게 한 번에 넣는 과정을 식으로 표현하면 다음과 같다.

\begin{Bmatrix} \vec{y_{1}} \\ \vec{y_{2}} \\ ... \\ \vec{y_{B}} \end{Bmatrix} = W \begin{Bmatrix} \vec{x_{1}} \\ \vec{x_{2}} \\ ... \\ \vec{x_{B}} \end{Bmatrix}

이렇게 만들어진 데이터의 갯수를 Batch size라고 한다. 즉 저기에서는 B값이라고 할 수 있다. 항상 train set과 test set을 연산할 때는 Batch size로 쪼개서 연산한다. 참고로 사람도 머리 좋으면 문제 많이 풀어도 괜찮듯이, 컴퓨터도 GPU의 성능에 따라서 내가 적용할 수 있는 Batch size가 더 커진다. 물론 컴 성능 안 좋다고 Batch size 줄이면 training 시간은 그만큼 늘어나니 참고하도록(...)

2) 실행

왠지는 모르겠지만 운 좋게 linear regression을 위한 데이터뎃이 준비되어 있다. 어떤 일인지 모르겠지만 있으니 일단 있으니 개꿀이다. ~~정 알고 싶으면 github repo의 dataset_making.py를 찾아볼 것.~~ .npy 파일로 준비되어 있으니, 지난번에 배운대로 데이터셋을 준비해 보자.

import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader
import os
from PIL import Image

class LinearRegressionDataset(Dataset):
    def __init__(self, train: bool):
        self.mode = "train" if train else "test"
        self.x = np.load("data/X_{}.npy".format(self.mode))
        self.y = np.load("data/Y_{}.npy".format(self.mode))
        
    def __len__(self):
        return len(self.x)
    
    def __getitem__(self, idx):
        return {"x": self.x[idx], 
                "y": self.y[idx]}

데이터셋을 준비는 해 놓았...다. 그러면 이것이 어떤 결과를 낼지 한 번 보자.

from dataset import LinearRegressionDataset

dataset = LinearRegressionDataset(train= True)
print(dataset[69])

이렇게 데이터셋의 임의의 인덱스를 로드하면,

❯ python3 experiment.py    
{'x': array([0.48587176, 0.25677657, 0.2848729 , 0.30728996]), 'y': array([ 1.78766776,  1.76768994, -0.29603695])}
(.env)

설명한 값과 같이 69번 직원의 역량과, 그들의 연봉, 보너스, 인망 값이 나온다.
이제 그들을 시험할 수 있는 training할 수 있는 weights값을 한 번 로드해보자.

model = nn.Linear(4,3)

그냥 상술한 y=Wx+b를 만드는 간단한 모델이다 y=model(x)를 하면 깔끔하게 y값이 나온다. 그러나 이 모델에는 심각한 문제가 있으니,

그냥 numpy 값이 아닌 torch.Tensor값을 사용해야 한다. pytorch 자체가 torch.Tensor라는 독자적인 텐서 체계를 사용하기 때문이다. 당연히 이 텐서끼리 더하고 빼고 지지고 볶고 하는 독자적인 방법이 numpy처럼 있으나, 이건 이 강의에서 넣지 않겠다. 요즘 구글링하거나 chatGPT 쨩에게 물어보면 다 알려주기 때문이다. 예를 들어 이렇게 하면

from dataset import LinearRegressionDataset
import numpy as np
import torch
import torch.nn as nn

dataset = LinearRegressionDataset(train= True)
input_val = np.random.rand(4)
model = nn.Linear(4,3)
ouput = model(input_val)

에러를 뿜뿜한다.

❯ python3 experiment.py
Traceback (most recent call last):
  File "/home/yeongyoo/practice_dl/linear_regression/experiment.py", line 9, in <module>
    ouput = model(input_val)
            ^^^^^^^^^^^^^^^^
  File "/home/yeongyoo/practice_dl/.env/lib/python3.12/site-packages/torch/nn/modules/module.py", line 1739, in _wrapped_call_impl
    return self._call_impl(*args, **kwargs)
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  File "/home/yeongyoo/practice_dl/.env/lib/python3.12/site-packages/torch/nn/modules/module.py", line 1750, in _call_impl
    return forward_call(*args, **kwargs)
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  File "/home/yeongyoo/practice_dl/.env/lib/python3.12/site-packages/torch/nn/modules/linear.py", line 125, in forward
    return F.linear(input, self.weight, self.bias)
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
TypeError: linear(): argument 'input' (position 1) must be Tensor, not numpy.ndarray
(.env)

그렇기 때문에 항상 input은 이렇게 바꿔줘야 한다.

input_val = torch.Tensor(np.random.rand(4))

아예 다들 custom dataset class에서 바꿔버리는 습관을 갖도록 하자.

# in dataset.py
    def __getitem__(self, idx):
        return {"input": torch.Tensor(self.x[idx]), 
                "label": torch.Tensor(self.y[idx])}

3. 그러면 training을 해 보자.

1) 이론

앞서 말한 과정을 기억하는가? 우리는 (1)과정만 했을 뿐이다. 당연히 아무것도 하지 않고 찍 모델 하나 선언하고 그냥 값을 넣으면 결과는 사실 제대로 나오지 않는다. 왜냐하면 여기 model에 있는 value에 있는 값들은 랜덤으로 생성되었으며, 전혀 보정되지 않았기 때문이다. 우리가 아무 공부도 안하고 수학문제를 풀면 그냥 다 찍은 거나 마찬가지 아니겠는가(...)

from dataset import LinearRegressionDataset
import numpy as np
import torch
import torch.nn as nn

dataset = LinearRegressionDataset(train= True)
data = dataset[69]
x, y = torch.Tensor(data["x"]), data["y"]
model = nn.Linear(4,3)
y_pred = model(x)
print("prediction:", y_pred)
print("answer:", y)

"""
❯ python3 experiment.py
prediction: tensor([-0.3009, -0.5141,  0.6458], grad_fn=<ViewBackward0>)
answer: [ 1.78766776  1.76768994 -0.29603695]
"""

그렇다면,

y_{1}=w_{11}x_{1}+ w_{12}x_{2}+ w_{13}x_{3}+w_{14}x_{4}+b

다시 이 식을 떠올려 보자. 여기서 위에서 표기한 salary, work hour... 값들은 쓰기 힘드니 숫자로 표기하였다. 여기서 우리는 정답 $\hat{y}$ 에 가까운 $y$ 값을 제대로 부여해 주는, $w$ 값들을 만들어야 한다.

L=|y_{1}-\hat{y}_{1}| + |y_{2}-\hat{y}_{2}| + |y_{3}-\hat{y}_{3}|

즉, 우리는 다음 L값이 최소가 되는 w값을 만들어야 한다. 그런데 우리 여기서 고등학교 수학 시간을 떠올려 보자. ~~중딩이라면 미안^^ 인공지능 생각하긴 아직 어린 나이니 재밌게 놀고 까까 사먹어라~~ 최솟값을 구하는 가장 정석적인 방법이 뭐였는가? 미분했을 때 값이 0이 나오는 것 아닌가? 그런데 절댓값이 있는 함수는 미분이 불가능하니까 우리 미분 가능하게 저 수식을 바꾸어 보도록 하자.

L=(y_{1}-\hat{y}_{1})^2 + (y_{2}-\hat{y}_{2})^2 + (y_{3}-\hat{y}_{3})^2

그렇다면 이걸 최소로 만드는 $w_{11}$ 값을 만들고 싶으면 어떻게 해야겠는가? $dL/dw_{11}=0$ 으로 하면 되지 않겠는가? 만약 다음과 같은 간단한 식이라면, 그렇게 만드는 $w_{11}$ 값을 찾기는 쉬울 것이다. 그러나 뒤를 보면 알겠지만, 우리가 하게 될 딥 러닝은 방정식 하나 띡 푸는 것만으로 $dL/dw_{11}=0$ 이 될 값을 구하게 되기 쉽지 않을 것이다. ~~아니 상식적으로 ChatGPT가 행렬 연산 한 번으로 딱 끝내서 값 내겠냐고~~ 그렇다면 어떻게 해야 할까?

w:=w-\gamma\frac{dL}{dw}

그렇다. 우리는 그냥 미분 값으로 현재의 기울기를 구한 다음에, 그 기울기만큼 값을 움직이는 전략을 사용하는 것이 최선의 선택이 될 것을 생각해볼 수 있다. 다음 그림과 같이 기울기가 크면 과감하게 움직여도 되지만, 기울기가 작으면 조금만 움직여야 기울기가 0인 쪽으로 최대한 움직일 수 있는 셈이다. 여기서 위 수식의 $\gamma$ 값, 즉 learning rate는 얼마나 많이 움직일지를 결정한다고 보면 된다. 당연히 이 learning rate는 너무 커서도 안 되고 작아서도 안 된다.

이 과정을 optimization이라고 한다. 한 챕터 풀면 채점하고 오답노트 풀듯, 이 optimization역시 한 batch마다 한다고 보면 된다. 이 과정을 train set의 모든 데이터에 따라 한 번 반복하는 것을 한 epoch이라고 한다. 즉, 다음 linear regression에서 deep learning이란 다음 값이 최솟값이 되는 적절한 weights값을 찾아 나서는 과정이고, 그것을 training이라 하는 것이다.

L=\sum_{b=1}^{B}(y_{b1}-\hat{y}_{b1})^2 + (y_{b2}-\hat{y}_{b2})^2 + (y_{b3}-\hat{y}_{b3})^2

그리고 여기서 최소가 되어야 하는 것을 loss function이라고 한다. 가장 적어야 하는 것이 잃어야 하는 것이지 얻어야 하는 것이 아니지 않는가?

2) 결론

다시 위에서 문제집 풀기에 비유한 과정을 deep learning에 대입해서 요약해보자.
1) 한 batch마다 input $x$ 에 대하여 결괏값 $y=f(x)$ 들을 도출한다.
2) $y$ 가 정답 라벨 $\hat{y}$ 에 얼마나 가까운지 그 Loss function을 추출해낸다.
3) loss function을 이용하여 정확도를 높이기 위한 f(x)의 변수들을 optimization한다.
4) 다시 주어진 input $x$ 에 대하여 결괏값 $y=f(x)$ 를 도출한다.
5) 정확도를 다시 측정하고 보정한다.
...무한반복...
6) 주어진 input $x$ 에 대하여 결괏값 $y=f(x)$ 를 도출하고, 그 정확도를 측정한다. 여기서는 시험이기 때문에 변수를 보정하지 않는다. 솔직히 수능 보고 오답노트 쓰는 미친 놈이 세상에 어디 있는가?
1) 이제 한 epoch가 끝났다. 다시 training을 한다.

그러면 이걸 실제 코드로 실행해보도록 하자.

3) 실행

그러면 이것들이 실제 상황에서 어떻게 굴러가는지 실행을 해 보도록 할까? 일단 dataset과, epoch 및 learning rate, 그리고 batch size를 뭘로 할지 설정하도록 하자.

EPOCH = 20
LEARNING_RATE = 1e-2
BATCH_SIZE = 64

그리고 이 dataset에 대해 문제가 있다. 이 데이터셋은 batch로 안 나뉘지 않았는가? 대체 어떻게 나눌지 감이 안 올 것이다. 걱정 붙들어 메시라. 그러라고 dataloader class가 있는 것이다. 사실 dataset class를 쓰는 가장 큰 이유는 dataloader class 때문이다.

train_dataset = LinearRegressionDataset(train= True)
test_dataset = LinearRegressionDataset(train= False)
train_dataloader = DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=True)
test_dataloader = DataLoader(test_dataset, batch_size=BATCH_SIZE, shuffle=True)

그러면 이제, model, loss function과 optimizer를 선언해 보자. 상술한 optimizing 방식은 가장 기초적인 방식인 (다른 방식도 많은데 결국에 다 여기서 나옴) SGD optimizing이다.

model = model = nn.Linear(4,3)
loss_function = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=LEARNING_RATE)

이제 이들을 이용해서 training을 해 보면 되겠다.

for epoch in range(1, EPOCH + 1):
    loss_val = 60
    
    # train
    model.train()
    for data in tqdm(train_dataloader, 
                     desc = "epoch {} and now loss {}...".format(epoch, loss_val)):
        label, x = data["label"], data["input"]
        pred = model(x)
        
        loss = loss_function(pred, label)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        
        loss_val = loss.item()

이제 여기서 model을 training시켜보자.
참고로 여기 있는 tqdm library progress bar를 보여줄 때 쓸만하니 써 보길 바란다. 주로 for문 안에서 for i in tqdm(long_list): 식으로 하면, for문 돌리는 도중에 progress bar를 보여준다.
당연히 loss는 loss_function(pred, label)로 구하면 된다. 다들 궁금한 건 밑에 세 줄일텐데, loss.backward()는 기울기를 계산하고, optimizer.step()는 torch.optim.SGD(model.parameters(), lr=LEARNING_RATE)에 등록된 모델의 가중치를 loss에 따라 optimization하고, optimizer.zero_grad()는 다음 반복을 위해 기울기를 초기화하는 과정이다. 일단 이 정도만 알아보자.

    model.eval()
    avg_test_loss = 0
    for data in tqdm(test_dataloader, 
                     desc = "epoch {} testing...".format(epoch, loss_val)):
        label, x = data["label"], data["input"]
        pred = model(x)
        
        loss = loss_function(pred, label)
        avg_test_loss += loss.item() / len(test_dataloader)

test할 때는 다음과 같이 loss function으로 optimization을 할 필요는 없고 그냥 loss 값만 확인해서 training이 얼마나 잘 되었는지만 알면 되겠다.

그렇다면, 이제, 얼마나 test가 잘 되어가고 있는지 확인해보자. training하고 test가 얼마나 잘 되었는지 확인하려면, 시각화 자료가 필요할 것이다. 시각화 자료도 얹어서 training하겠다. 참고로 여기서 import matplotlib.pyplot라이브러를 가져올 건데 얼마나 이 라이브러리의 기본 설명은 생략하겠다. 구글링이나 GPT에게 물어보기를 하면 나보다 6000배는 더 잘 알려준다.

avg_train_losses = []
avg_test_losses = []
for epoch in range(1, EPOCH + 1):
    loss_val = 60
    
    #train
    batch_losses = []
    model.train()
    for i, data in tqdm(enumerate(train_dataloader), 
                     desc = "epoch {} training...".format(epoch)):
        label, x = data["label"], data["input"]
        pred = model(x)
        
        loss = loss_function(pred, label)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        
        batch_losses.append(loss.item())
        avg_train_losses.append(sum(batch_losses) /(i+1))
    
    #test
    model.eval()
    avg_test_loss = 0
    for data in tqdm(test_dataloader, 
                     desc = "epoch {} testing...".format(epoch, loss_val)):
        label, x = data["label"], data["input"]
        pred = model(x)
        
        loss = loss_function(pred, label)
        avg_test_loss += loss.item() / len(test_dataloader)
        
    avg_test_losses.append(avg_test_loss)
        
    print("EPOCH {} TEST LOSS: {}".format(epoch, avg_test_loss))
    
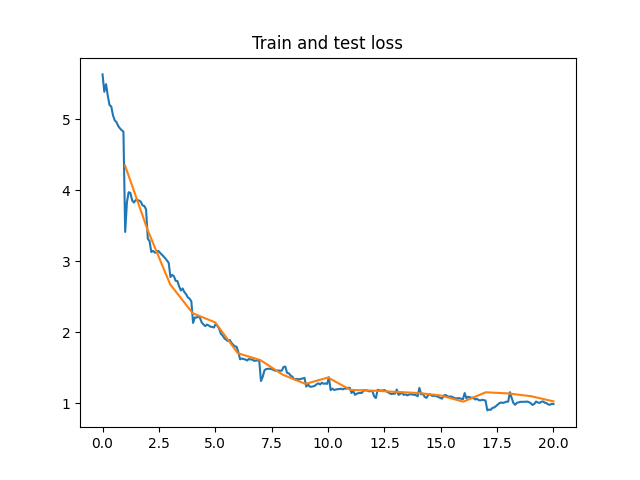
plt.plot(np.linspace(0, EPOCH, EPOCH*len(train_dataloader)), avg_train_losses, label="train")
plt.plot(list(range(1, EPOCH+1)), avg_test_losses, label="test")
plt.title("Train and test loss")
plt.savefig("plot.png")