수식트리(Expression Tree)

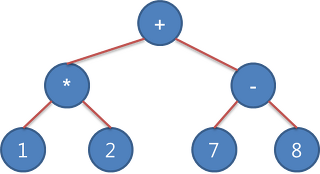
• 중위 표기법의 수식을 수식 트리로 변환하는 프로그램을 작성하는것이 목적
• 중위 표기법 수식은 사람이 이해하기 쉽지만 기계가 인식하기에는 어려움 반면에 수식 트리는 해석이 쉬움
• 연산 과정에서 연산자의 우선순위 고려가 필요 없음
• 가운데 루트노드 자리가 연산자, 아래의 하위 노드가 피연산자 역할을 하게 됨
• 이진트리 순회 방법에 따라 전위, 중위, 후위표기법을 나타낼 수 있음
• 후위표기법을 트리로 변환, 중위표기법을 경우 후위표기법으로 변환한 후 트리로 변환

구현

import java.util.Stack;

public class ExpressionTree {

    private BTreeNode root;

    public BTreeNode getExpressionTree(String exp) {
        /* 후위표기법 -> 수식 트리로 변경 : 수식트리의 루트노드만 리턴받으면 됨 */
        char[] data = exp.toCharArray();
        int length = data.length;

        Stack temp = new Stack();
        for (int i = 0; i < length; i++) {
            char target = data[i];

            if(target >= '0' && target <= '9'){
                temp.push(target);
            } else {
                BTreeNode newNode = new BTreeNode(target);

                Object sub = temp.pop();
                newNode.setRightSubTree(sub instanceof BTreeNode ? (BTreeNode)sub : new BTreeNode(sub));
                sub = temp.pop();
                newNode.setLeftSubTree(sub instanceof BTreeNode ? (BTreeNode)sub : new BTreeNode(sub));
                temp.push(newNode);
            }
        }

        root = (BTreeNode)temp.pop();
        return root;
    }


    public int getResult(BTreeNode root){
        if(root.getLeftSubTree() == null && root.getRightSubTree() == null){
            return Integer.parseInt(root.getData().toString());
        }

        int left = getResult(root.getLeftSubTree());
        int right = getResult(root.getRightSubTree());

        switch((char)root.getData()){
            case '+':
                return left+right;

            case '-':
                return left-right;

            case '*':
                return left*right;

            case '/':
                return left/right;
        }

        return 0;
    }


    public void getPrefix(BTreeNode root){
        BTreeNode.preorderTreverse(root);
    }

    public void getInfix(BTreeNode root){
        BTreeNode.inorderTraverse(root);
    }

    public void getPostfix(BTreeNode root){
        BTreeNode.postorderTreverse(root);
    }

}



/* BTreeNode 표기법 관련 코드 : 순회 순서만 변경해주면 됨 */

public static void preorderTreverse(BTreeNode root){
    if(root == null){
        return;
    }

    System.out.print(root.getData());
    preorderTreverse(root.getLeftSubTree());
    preorderTreverse(root.getRightSubTree());
}

public static void inorderTraverse(BTreeNode root){
    /* [이진트리 관점] */
    if(root == null){
        return;
    }

    inorderTraverse(root.getLeftSubTree());
    System.out.print(root.getData());
    inorderTraverse(root.getRightSubTree());

    /*
    [단순 노드 관점]
    if(root.leftSubTree != null){
        Traverse(root.leftSubTree);
    }
    System.out.println(root.getData());
    if(root.rightSubTree != null){
        Traverse(root.rightSubTree);
     }
     */
}

public static void postorderTreverse(BTreeNode root){
    if(root == null){
        return;
    }

    postorderTreverse(root.getLeftSubTree());
    postorderTreverse(root.getRightSubTree());
    System.out.print(root.getData());
}

우선순위큐(Priority Queue)

• PriorityQueue는 우선순위를 먼저 결정하고 그 우선순위가 높은 엘리먼트가 먼저 나가는 자료구조
• 우선순위 큐는 힙을 이용하여 구현
• 데이터를 삽입할 때 우선순위를 기준으로 최대힙 혹은 최소 힙을 구성
• 데이터를 꺼낼 때 루트 노드를 얻어낸 뒤 루트 노드를 삭제할 때는 빈 루트 노드 위치에 맨 마지막 노드를 삽입한 후 아래로 내려가면서 적절한 자리를 찾아서 옮기는 방식

특징

1. 높은 우선순위의 요소를 먼저 꺼내서 처리하는 구조 (큐에 들어가는 원소는 비교가 가능한 기준이 있어야함)
2. 내부 요소는 힙으로 구성되어 이진트리 구조로 이루어져 있음
3. 내부구조가 힙으로 구성되어 있기에 시간 복잡도는 O(NLogN)
4. 응급실과 같이 우선순위를 중요시해야 하는 상황에서 쓰임

JAVA에서 제공하는 함수

선언

import java.util.PriorityQueue; //import

//int형 priorityQueue 선언 (우선순위가 낮은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();

//int형 priorityQueue 선언 (우선순위가 높은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

//String형 priorityQueue 선언 (우선순위가 낮은 숫자 순)
PriorityQueue<String> priorityQueue = new PriorityQueue<>(); 

//String형 priorityQueue 선언 (우선순위가 높은 숫자 순)
PriorityQueue<String> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

• 자바에서 우선순위 큐 라이브러리를 사용하고 싶다면 java.util.PriorityQueue를 import 하고 Queue<Element> queue = new Queue<>()와 같은 형식으로 선언하면 됨.
• 기본은 우선순위가 낮은 숫자가 부여되고 만약 높은 숫자가 우선순위가 되게 하고 싶다면 선언 시 Collections.reverseOrder() 사용

값 추가

priorityQueue.add(1);     
priorityQueue.add(2);     
priorityQueue.offer(3);   

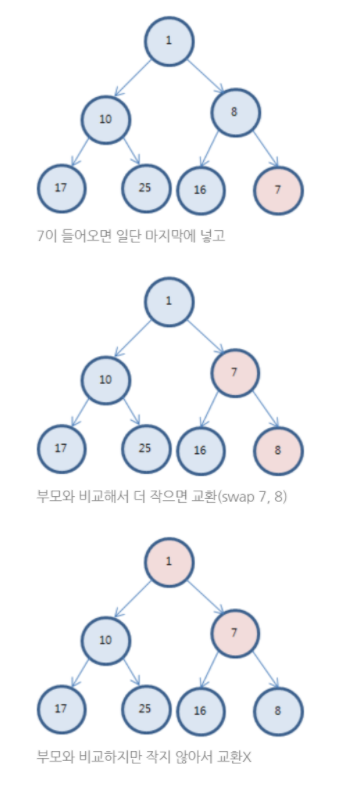
• 우선순위 큐에 값을 추가하고 싶다면 add(value) 또는 offer(value) 사용
• add(value) 메서드의 경우 만약 삽입에 성공하면 true를 반환하고, 큐에 여유 공간이 없어 삽입에 실패하면 IllegalStateException을 발생
• 우선순위 큐에 값을 추가한다면 즉시 정렬됨

값 제거

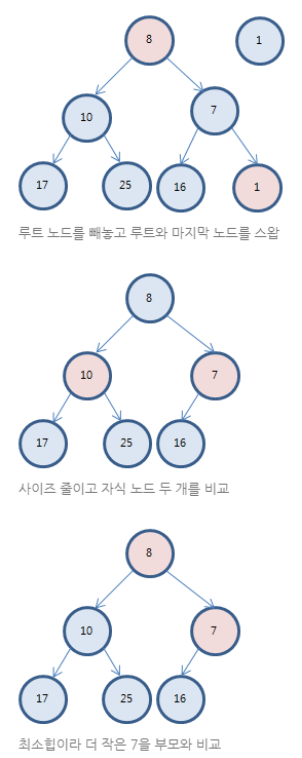
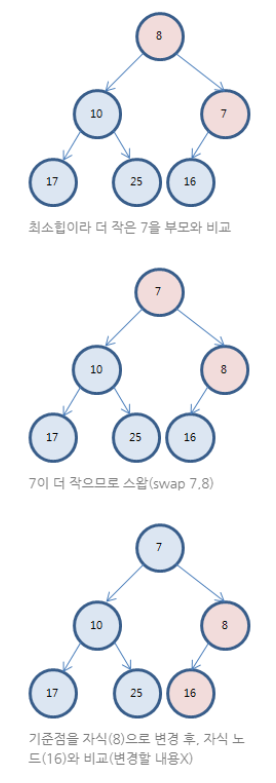
• poll()이나 remove() 사용.
• 값을 제거할 시 우선순위가 가장 높은 값이 제거
• poll() 함수는 우선순위 큐가 비어있으면 null을 반환
• pop을 하면 가장 앞쪽에 있는 원소의 값이 제거
• 모든 요소를 제거하려면 clear() 사용

Priority Queue에서 우선순위가 가장 높은 값 출력

PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();//int형 priorityQueue 선언
priorityQueue.offer(2);     // priorityQueue에 값 2 추가
priorityQueue.offer(1);     // priorityQueue에 값 1 추가
priorityQueue.offer(3);     // priorityQueue에 값 3 추가
priorityQueue.peek();       // priorityQueue에 첫번째 값 참조 = 1

• Priority Queue에서 우선순위가 가장 높은 값을 참조하고 싶다면 peek() 사용