BPTT

홍종현·2022년 4월 27일

Deep Learning & Machine Learning

목록 보기
1/3

Backpropagation Through Time

BPTT는 RNN에서 계산되는 back propagation이다. RNN의 구조는 sequential하기 때문에 이에 따라 발생하는 hidden state를 따라 역행하면서 전파되는 gradient의 계산 방법이다. 다음은 RNN의 기본 구조이다.

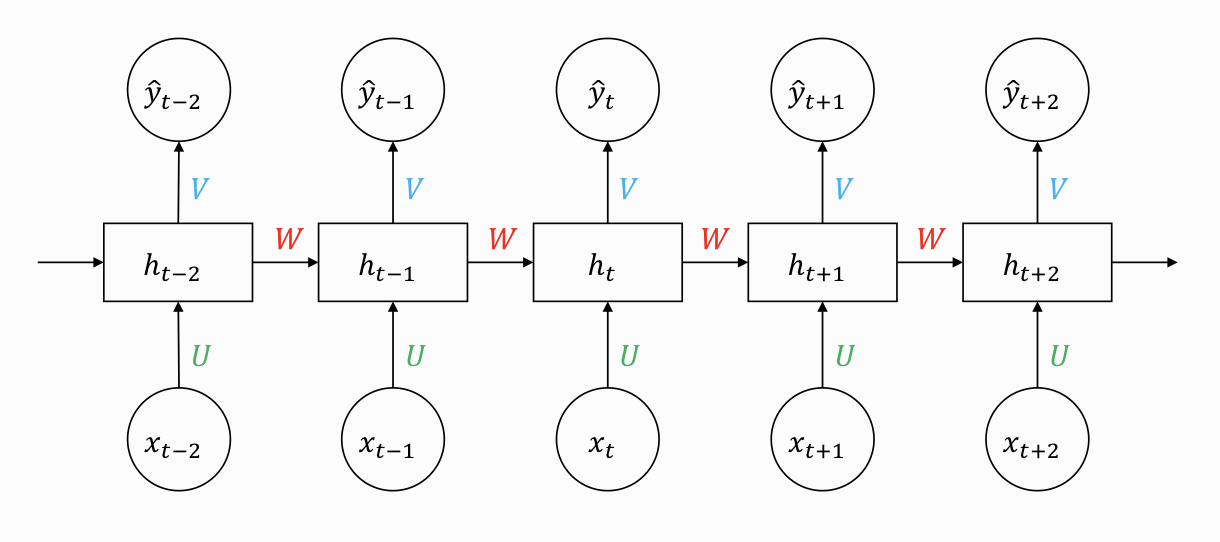
st=tahn(Uxt+Wst−1)s_t = tahn(Ux_t + W_{s_{t-1}})
ytˉ=sotfmax(Vst)\bar{y_t} = sotfmax(Vs_t)

UU: input을 연결하는 가중치 행렬
WW: 현재 hidden state와 다음 hidden state를 연결하는 가중치 행렬
VV: output을 연결하는 가중치 행렬

이때 첫번째 셀의 loss값을 다음과 같이 정리할 수 있다.

E1=(d1ˉ−y1ˉ)2E_1 = (\bar{d_1} -\bar{y_1})^2

만약 Timestep = 3이라면 현재 model에서 update해야되는 weight matrix는 UU, WW, VV 3개가 존재합니다.

그렇다면 UU의 gradient를 구하기 위하여 E3E_3에 대하여 UU로 편미분한 결과를 chain rule을 통해 구할 수 있다.

∂E3∂U=∂E3∂y3ˉ⋅∂y3∂U\frac{\partial E_3}{\partial U} = \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial U}

다음 WW의 gradient를 구하면 다음과 같다.

∂E3∂W=∂E3∂y3ˉ⋅∂y3∂W\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial W}
∂E3∂W=∂E3∂y3ˉ⋅∂y3∂s3⋅∂s3∂W\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial W}

하지만 기존 backpropagation과는 다른 점이 각 timestep이 gradient에 영향을 주었기 때문에 ∂s3∂W\frac{\partial s_3}{\partial W}를 상수 취급할 수 없다. 현재 timestep이 3인 출력 부분까지의 이전 timestep이 적용되기 때문에 t=2, t=1 까지 gradient를 전부 더해야한다. 그렇다면 다음과 같이 정리할 수 있다.

∂E3∂W=∂E3∂y3ˉ⋅∂y3∂s3⋅∂s3∂W+∂E3∂y3ˉ⋅∂y3∂s3⋅∂s3∂s2⋅∂s2∂W+∂E3∂y3ˉ⋅∂y3∂s3⋅∂s3∂s2⋅∂s2∂s1⋅∂s1∂W\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial W} + \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial W} + \frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial s_1} \cdot \frac{\partial s_1}{\partial W}

간단하게 정리하면 다음과 같은 식으로 정리할 수 있다.

∂E3∂W=∑i=03∂E3∂y3ˉ⋅∂y3∂s3⋅∂s3∂si⋅∂si∂W\frac{\partial E_3}{\partial W} = \sum^3_{i=0}\frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_i} \cdot \frac{\partial s_i}{\partial W}

그리고 ∂s3∂si\frac{\partial s_3}{\partial s_i}도 chain rule을 내포하고 있기 때문에 ∂s3∂si=∂s3∂s2⋅∂s2∂s1\frac{\partial s_3}{\partial s_i} = \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial s_1}로 나타낼 수 있다. 위의 gradient를 다시 써보면 다음과 같이 나타낼 수 있다.

∂E3∂W=∑i=03∂E3∂y3ˉ⋅∂y3∂s3(∏j=i+13∂sj∂sj−1)⋅∂si∂W\frac{\partial E_3}{\partial W} = \sum^3_{i=0}\frac{\partial E_3}{\partial \bar{y_3}} \cdot \frac{\partial y_3}{\partial s_3} \bigg( \prod^3_{j=i+1}\frac{\partial s_{j}}{\partial s_{j-1}}\bigg) \cdot \frac{\partial s_i}{\partial W}

하지만 BPTT를 진행하다보면 처음부터 끝까지 모든 loss를 backpropagation해야하기 때문에 계샨량이 너무 많아지는데, 이것을 줄이고자 Truncated-Backpropagation Through Time(생략된-BPTT)를 많이 사용한다.

profile
홍종현
다음 포스트

Tensor Manipulation

0개의 댓글