차원 축소 - PCA

홍종현·2022년 2월 25일

Deep Learning & Machine Learning

목록 보기

3/3

0. Introduction

오늘은 차원 축소의 기법중 하나인 PCA에 대해 알아보고자 한다. 차원 축소를 알아보기전에 먼저 차원의 저주를 알아야하는데 차원의 저주란 입력된 데이터의 수보다 데이터의 차원이 더 큰 경우 발생하는 문제이다. 우리는 데이터, 벡터가 존재하는 공간에서 분류 혹은 예측을 하는 가장 적합한 함수를 찾는것이 목적이다. 그러나 입력한 데이터의 양보다 데이터의 차원이 많아지게되면 이 벡터들을 분류하고 예측하는 함수의 모형이 복잡해지게 된다. 이렇게 되면 모델의 복잡도가 증가하게되고 성능 또한 낮아진다.

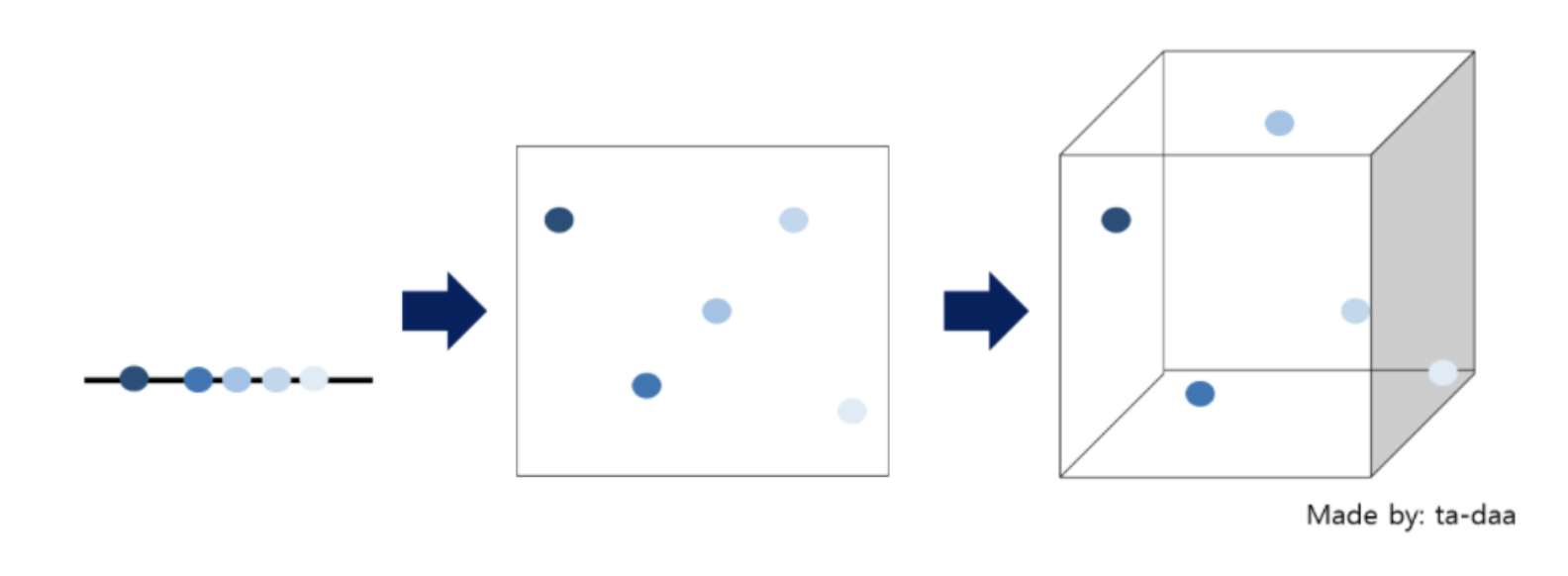
위의 그림을 보면 차원이 증가함에 따라 벡터 사이의 거리들이 멀어져 빈공간이 생기는 것을 알 수 있다. 이러한 빈공간을 채우기 위해 차원을 축소하거나 데이터를 많이 획득해야한다. 이러한 차원을 축소 하는 기법에는 Feature Selection과 Feature Extraction이 있는데 PCA는 Feature Selection기법 중 하나이며 주성분 분석이라고도 불린다.

1. Why?

저차원에 투영하는데 있어 다른 방향으로 투영하는것이 아니라 분산을 최대로 보존할 수 있는 축을 기준으로 할때, 정보를 가장 적게 손실할 수 있다.

분산이 커져야 관측치들의 차이점이 더 명학해진다.

2. PCA

PCA는 데이터의 분산을 최대한 보존하면서 서로 직교하는 축을 찾아 고차원을 저차원으로 선형 변환하는 기법이다. 쉽게 말하면 데이터의 특성과 다양성, 분산을 가장 보전하는 성분을 추출하는 것이 PCA기법이다.예를 들어, feature가 총 2개를 가지고 있는 2차원의 데이터를 다음과 같이 표현했을때 다음과 같다.

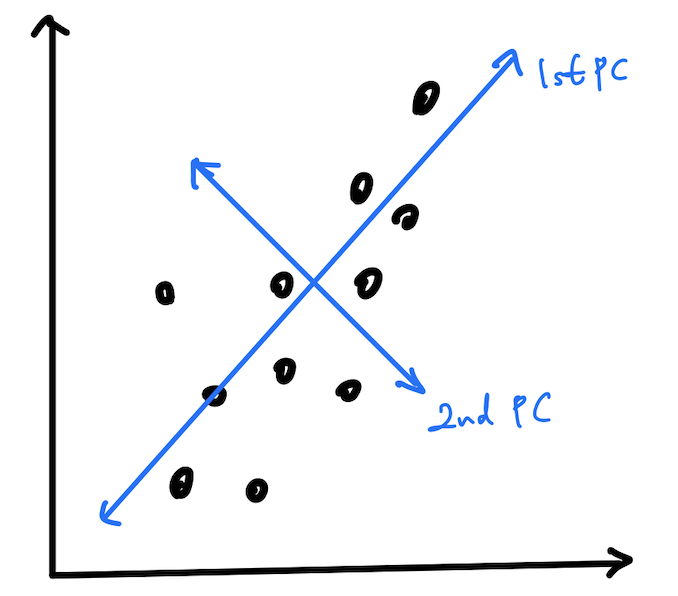
분산을 가장 잘 보존할 수 있는 방향을 찾습니다. 그리고 그 분산이 가장 커지는 축을 1st Principal Component로 설정하고 그 축과 직교하는 축을 2nd Principal Component로 설정하여 데이터를 선형 변환한다.이것을 쉽게 설명하면 데이터를 1st Principal Component에 정사영을 시키면 1차원이기 때문에 겹치는 데이터들이 생기게된다. 이 겹치는 데이터를 표현해주기 위해 그와 직교하는 축인 2nd Principal Component에 사영을 시키게되면 겹치는 데이터를 표현할 수 있게된다.

예를 들어, PCA는 변수 $p$ 개, $n$ 개의 데이터가 존재하는 $X$ (pxn)로 새로운 feature $b$ 를 만드는 식을 아래와 같이 표현할 수 있다.

\overrightarrow{b_1}=a_{11}\overrightarrow{x_1} + a_{12}\overrightarrow{x_2} + \cdots + a_{1p}\overrightarrow{x_p} = \overrightarrow{a1^T}X

\overrightarrow{b_2} = a_{21}\overrightarrow{x_1} + a_{22}\overrightarrow{x_2} + \cdots + a_{2p}\overrightarrow{x_p} = \overrightarrow{a2^T}X

\overrightarrow{b_3} = a_{31}\overrightarrow{x_1} + a_{32}\overrightarrow{x_2} + \cdots + a_{3p}\overrightarrow{x_p} = \overrightarrow{a3^T}X

$\cdot$

\overrightarrow{b_p} = a_{p1}\overrightarrow{x_1} + a_{p2}\overrightarrow{x_2} + \cdots + a_{3pp}\overrightarrow{x_p} = \overrightarrow{ap^T}X

위의 식은 벡터 $b_i$ 는 X라는 데이터를 $a_i$ 라는 새로운 축에 사영을 시킨 식이다. 이러한 PCA로 새롭게 만들어진 $B$ 는 다음과 같은 식으로 적을 수 있다.

Z = A^TX

2.1 공분산 행렬과 고유벡터, 고유 값

PCA를 하기전에 공분산 행렬과 고유 벡터, 고유 값에 대해 먼저 알아야 한다. 공분산 행렬이란 쉽게 말해서 사각행렬의 성분을 각 변수의 분산(주대각선)과 공분산으로 채운 행렬이다. 공분산이란, 둘 이상의 변량이 연관성을 가지며 분포하는 모양을 전체적으로 나타낸 분산을 의미한다. 예를 들어, 확률 변수 X와 Y가 있을 때 다음과 같이 정리할 수 있다.

X와 Y의 기댓값 $E(X) = \mu, E(Y) = v$

Cov(X,Y) = E((X-\mu)(Y-v))

공분산 행렬이란, 데이터가 행렬 $X$ 로 표현될 때,

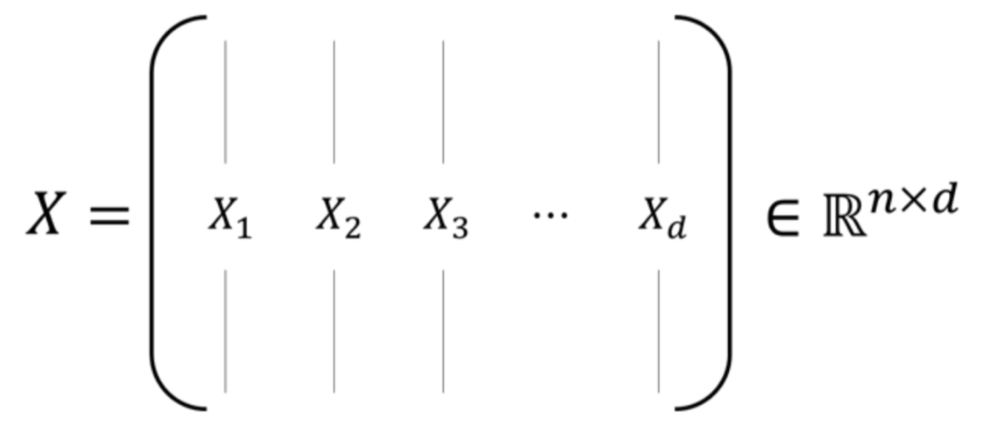
다음과 같이 내적 연산을 해서 특징이 얼마나 유사한지 나타내준다.

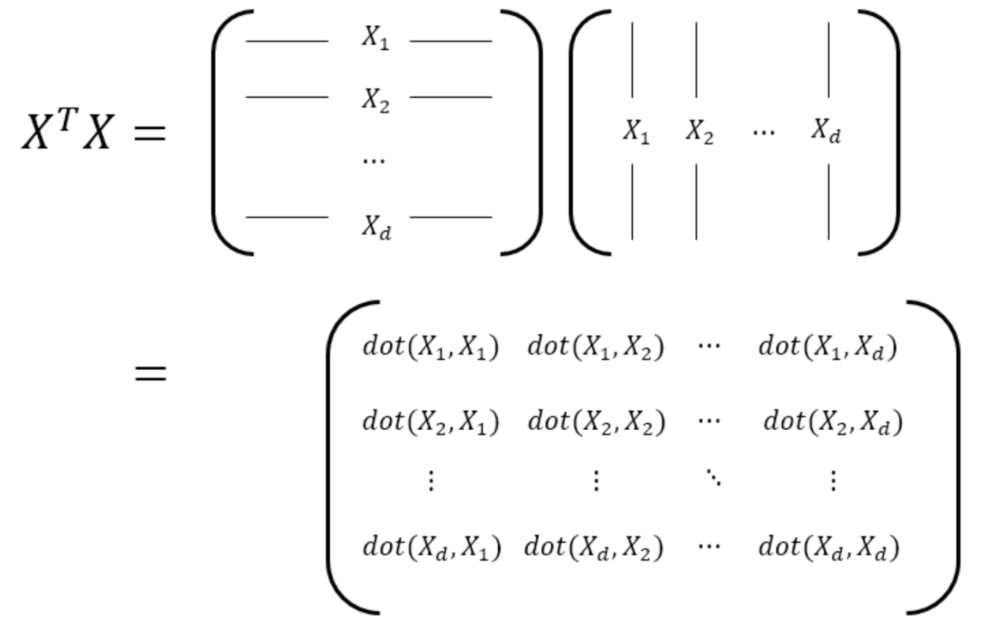
공분산 행렬에서 고유 벡터와 고유 값을 찾는것은 결국 데이터의 주성분을 찾는것과 동일하다. 그 이유는 고유 벡터는 행렬이 어떤 방향으로 힘을 가하는지 나타내고, 이것은 결국 어떤 방향으로 분산이 가장 큰지 알 수 있다. 고유 값은 고유 벡터에 해당하는 상관 계수이다. 공분산 행렬에서 고유 값은 각 축에 대한 공분산 값이 되고 고유 값이 큰 순서대로 고유 벡터를 정렬하면 크기 순서대로 주성분을 구하는것과 같다.

데이터가 각 변수별로 평균이 0(centering)이라고 할 때 데이터 $X$ 의 공분산 행렬 $C$ 는 다음과 같이 구할 수 있다. 이때 $\bar{X}$ 는 각 변수의 평균 값이다.

C = cov(X) = \frac{1}{n}(X-\bar{X})(X-\bar{X})^T

데이터 X의 shape가 p x n이라면 공분산 행렬 $C$ 는 p x p크기의 정방행렬이 됩니다. 또한 $C^T = C$ 인 대칭행렬이다.

고유벡터와 고유 값이란 행렬 $A$ 가 주어졌을 때, 스칼라 값 $\lambda$ 와 벡터 $x$ 가 밑에와 같은 식을 만족할 때, 고유값과 고유벡터를 정의할 수 있다.

Ax=\lambda x \Longrightarrow (A- \lambda I)x = 0

행렬 $A$ 에 벡터 $x$ 를 곱한다는 뜻은 선형변환 한다는것을 의미하는데, 이때 크기만 달라지고 방향은 같은 벡터들을 고유벡터, eigenvector라고 하고 변화한 크기, $\lambda$ 를 고유 값이라고 한다. 그리고 고유벡터들은 전부 다 직교한다는 특징을 갖고 있고 그러므로 다음과 같은 식을 나타낼 수 있다.

x_i^Tx_j = 0

2.2 PCA Progress

PCA를 하기위해 제일 먼저 각 변수들의 평균을 0으로 만들어줘야 하는데 이러한 작업을 'centering' 혹은 'normalization'이라고 한다. 머신러닝과 딥러닝 알고리즘을 훈련하기 위해 꼭 필요한 작업이다. 각 feature마다 값의 범위가 다르기 때문에 scaling과 비슷한 의미로 사용되는거같다.

공분산 행렬을 구하는 식은 다음과 같다.

C = cov(X) = \frac{1}{n}(X-\bar{X})(X-\bar{X})^T

에서 좌변인 $(X-\bar{X})$ 의 식을 통해 data cenetering을 한다.

그 다음 벡터 $x$ 가 기저 $w$ 에 사영 되었을 때, 그 분산을 구하는 식을 다음과 같이 나타낼 수 있다. 이때 $V$ 는 분산 $C$ 는 데이터 $X$ 의 표본 분산의 공분산 행렬이다.

V = \frac{1}{n}(w^TX)(w^TX)^T = \frac{1}{n}w^TXX^Tw = w^TCw

Maximize $V$ -> Maximize $w^TCw$

이 때 PCA는 이 분산 값 $V$ 의 최대 값을 구하는 것이 목적이다. 위의 식을 만족 시키는 $w$ 는 무수히 많고 $w$ 의 크기를 키우면 $V$ 의 최대값이 될 수 도 있어 제약식을 통해 제약을 걸어준다. 이 기저의 크기를 1로 맞추는 제약식은 다음과 같다.

L = w^Tw = 1

로 둔다.

Lagrange Multiplier

그런 다음 라그랑주 승수법을 이용해 제약조건 하에서 최대 분산을 구해줘야하는데 라그랑주 승수법은 다음과 같다.

w^TCw

s.t. w^Tw = 1

위 식은 $w^Tw = 1$ 인 제약 조건 하에서 f의 최대값을 구하는 식일 때, 최적화 문제를 해결하기 위한 방법으로 $\lambda$ (Lagrange Multiplier)를 이용해 $L$ 에 대해 식을 나타낼 수 있다.

L = wTCw + \lambda (w^Tw-1)

함수 $L$ 에 대해 w에 대한 이차 함수이면서 최대 값을 구해야 되는 함수이니까 극대 혹은 극소점에서는 $w$ 에 대한 미분값이 0이여야된다. 그러면 다음과 같은 식을 구할 수 있다.

\frac{\partial L}{\partial w} = 0 \Longrightarrow Cw - \lambda w = 0 \Longrightarrow (C- \lambda I)w = 0

이 때 $w$ 는 공분산 행렬 $C$ 의 고유 벡터이고 $\lambda$ 는 $C$ 의 고유 값이 된다.

이제 위에서 구한 고유 벡터를 원래 데이터 $X$ 에 사영시키면 다음과 같은 식을 통해 사영시킨 후의 분산을 구할 수 있다.

v = (w_1^TX)(w_1^X)T = w_1^TXX^Tw_1 = w_1^TCw_1

Cw_1 = \lambda_1 w_1 \Longrightarrow w_1^TCw_1 = w_1^T \lambda_1 w_1 = \lambda_1 w_1^T w_1 = \lambda_1

위의 식을 통해 $w_1$ 에 사영된 데이터의 분산은 $\lambda$ _1이 된다. 다시 말해, $\lambda_1$ 은 $w_1$ 에 기저를 시켰을 때, 보존되는 분산량이다. 그렇다면 첫번째 분산인 $\lambda_1$ 과 $\lambda_2$ 를 더해서 $\lambda_1$ 을 나누어 준다면 2차원 데이터를 첫번째 주성분에 사영시키면 원 데이터의 보존량 $Y$ 를 구할 수 있다. 고유값이 만약 [ $\lambda_1, \lambda_2$ ]일 경우 아래의 식과 같다.

Y = \frac{ \lambda_1 }{ \lambda_1 + \lambda_2 }

PCA를 통해 차원축소를 할 때, 축소될 차원을 선택하는 기준은 전체 data의 분산의 90% 정도까지만 반영하는 차원 k를 찾는것이 default라고 알고 있다.

홍종현

이전 포스트