자료구조 - 그래프(Graph)

1. 그래프의 정의

연결되어 있는 정점와 정점간의 관계를 표현할 수 있는 자료구조.
출처: [천재학습백과]

2. 자료구조에 따른 용법

비선형 구조 => 표현에 초점
선형구조 => 자료를 저장하고 꺼내는 것에 초점
그래프 => 연결 관계에 초점

3. 그래프의 용어 정리

노드(Node): 연결 관계를 가진 각 데이터를 의미. 정점(Vertex)이라고도 한다.
간선(Edge): 노드 간의 관계를 표시한 선.
인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)

4. 그래프의 종류

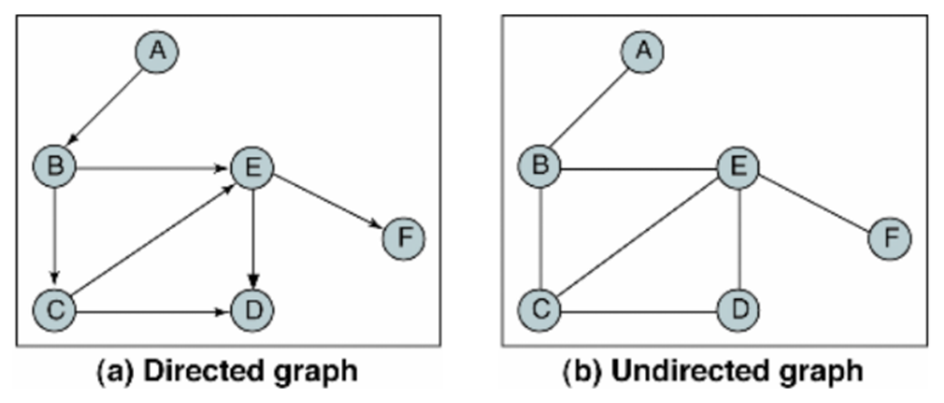
유방향 그래프(Directed Graph): 방향이 있는 간선을 갖는다. 간선은 단방향 관계를 나타내며, 각 간선은 한 방향으로만 진행할 수 있다.
무방향 그래프(Undirected Graph): 방향이 없는 간선을 갖는다.

자료 1) 그래프의 종류

5. 그래프의 표현 방법

: 그래프라는 개념을 코드로 표현하는 방법은 두 가지 방법이 있다

1) 인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현
2) 인접 리스트(Adjacnecy List): 링크드 리스트로 그래프의 연결 관계를 표현

이를 예시를 통해 알아보자

자료 2) 표현 방법의 예시

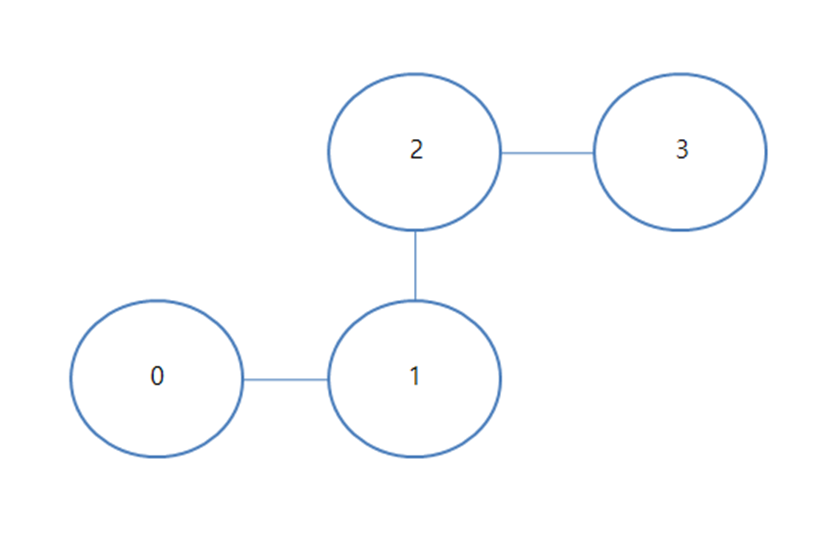
다음과 같은 그래프가 주어질 때 이를 인접행렬, 인접리스트로 나타내면 다음과 같다

• 1. 인접 행렬(2차원 배열)

   0  1  2  3                                graph = [
0  x  o  x  x                                   [False, True, False, False],
1  o  x  o  x             =>                    [True, False, True, False],
2  x  o  x  o                                   [False, True, False, True],
3  x  x  o  x                                   [False, False, True, False],
                                         	 ]

• 2. 인접리스트

graph = {
	0: [1],
	1: [0, 2],
	2: [1, 3],
	3: [2],
}

• 두방식의 차이

  인접 행렬으로 표현하면 즉각적으로 0과 1이 연결되었는지 여부를 바로 알 수 있다. 그러나, 모든 조합의 연결 여부를 저장해야 되기 때문에 O(노드^2) 만큼의 공간을 사용해야 한다.

  반면에 인접 리스트로 표현하면 즉각적으로 연결되었는지 알 수 없고, 각 리스트를 돌아봐야 한다. 따라서 연결되었는지 여부를 알기 위해서 최대 O(간선) 만큼의 시간을 사용해야 한다. 대신 모든 조합의 연결 여부를 저장할 필요가 없으니 O(노드 + 간선)만큼의 공간이 사용된다.