자료구조 - 힙(Heap)

힙

힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조(tree-based structure)
-위키백과
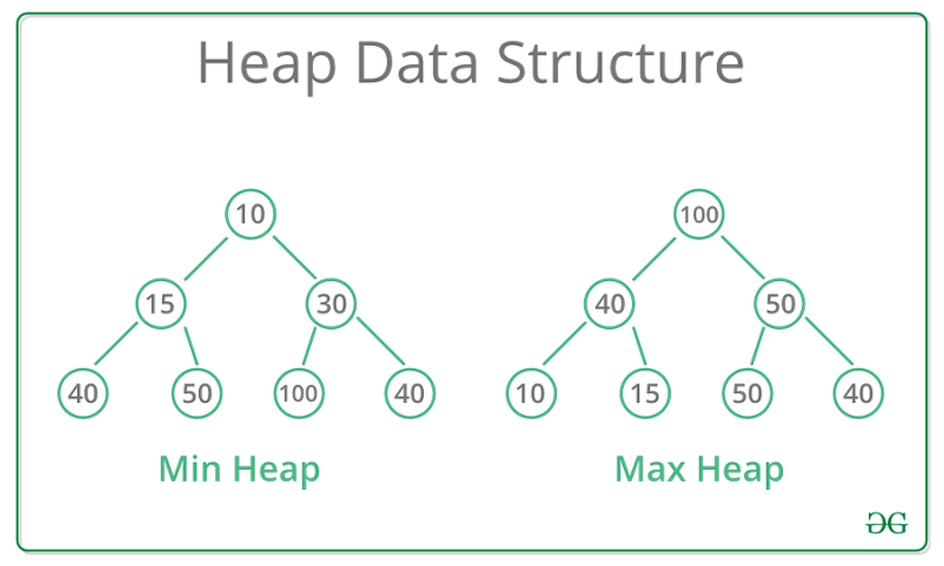
이때 최대값이 맨 위에 있는 트리를 Max heap, 최소값이 맨 위에 있는 트리를 Min heap이라고 한다.

힙의 메소드

: Max heap과 Min heap의 규칙이 지켜지면서 추가 또는 삭제 해야한다.

1. 원소추가(insert) => O(log(n))의 시간 복잡도를 갖는다.

• 맨 마지막에 노드를 추가한다
• 부모 노드와 비교한다. 비교 후 자리를 찾아준다
• 루트 노드까지 위의 과정을 반복한다

2. 원소제거(delete) => O(log(n))의 시간 복잡도를 갖는다.

• 루트 노드와 맨 뒤의 노드를 교체한다.
• 맨 뒤의 노드(원래 루트 노드)를 삭제한다.
• 3. 변경된 노드와 자식 노드와 비교한다. 비교 후 자리를 찾아준다.
     이때 자식 노드끼리 비교 후, 둘 중 큰 것과 부모노드의 자리를 교체한다
• 위 과정을 반복한다.
• 2에서 제거한 루트 노드를 반환해준다.

코드 구현(Max Heap)

class MaxHeap {
  constructor() {
    this.items = [null];
  }

  insert(data) {
    // 노드의 가장 끝부분에 data를 넣어줌
    this.items.push(data);
    let currentIdx = this.items.length - 1;

    // currentIdx가 가장 상단, 즉 idx가 1보다 클때까지 반복
    while (currentIdx > 1) {
      const parentIdx = currentIdx / 2; // 부모 노드의 idx

      if (this.items[currentIdx] > this.items[parentIdx]) {
        const tempItem = this.items[currentIdx];
        this.items[currentIdx] = this.items[parentIdx];
        this.items[parentIdx] = tempItem;
        currentIdx = parentIdx;
      } else {
        break;
      }
    }
    return;
  }

  delete() {
    const maxNode = this.items[1];

    this.items[1] = this.items[this.items.length - 1];
    this.items.pop();

    let currentIdx = 1;

    while (currentIdx < this.items.length) {
      const idxChildNodeL = currentIdx * 2; // 현재 노드의 왼쪽 자식 노드의 idx
      const idxChildNodeR = currentIdx * 2 + 1; // 현재 노드의 오른쪽 자식 노드의 idx
      let idxBiggestNode = currentIdx;

      // 가장 큰 노드의 idx를 찾기위해
      if (
        idxChildNodeL < this.items.length &&
        this.items[idxChildNodeL] > this.items[idxBiggestNode]
      ) {
        idxBiggestNode = idxChildNodeL;
      }

      // 역시 가장 큰 노드의 idx를 찾기위해
      if (
        idxChildNodeR < this.items.length &&
        this.items[idxChildNodeR] > this.items[idxBiggestNode]
      ) {
        idxBiggestNode = idxChildNodeR;
      }

      // 가장 큰 노드의 idx와 현재 노드의 idx가 같다? => 현재 상태가 maxheap의 상태다. 따라서 break
      if (currentIdx == idxBiggestNode) {
        break;
      }

      // 노드의 자리를 바꿔주는 부분
      const needToChange = this.items[currentIdx];
      this.items[currentIdx] = this.items[idxBiggestNode];
      this.items[idxBiggestNode] = needToChange;

      currentIdx = idxBiggestNode;
    }

    return maxNode;
  }
}