백준 1655번: 가운데를 말해요

문제

• https://www.acmicpc.net/problem/1655
• 최대힙과 최소힙을 함께 사용해 전체 집합의 중앙값 확인하기

기록 포인트

• 최대힙과 최소힙을 함께 사용해 전체 집합의 중앙값을 확인하는 방법

접근 방식

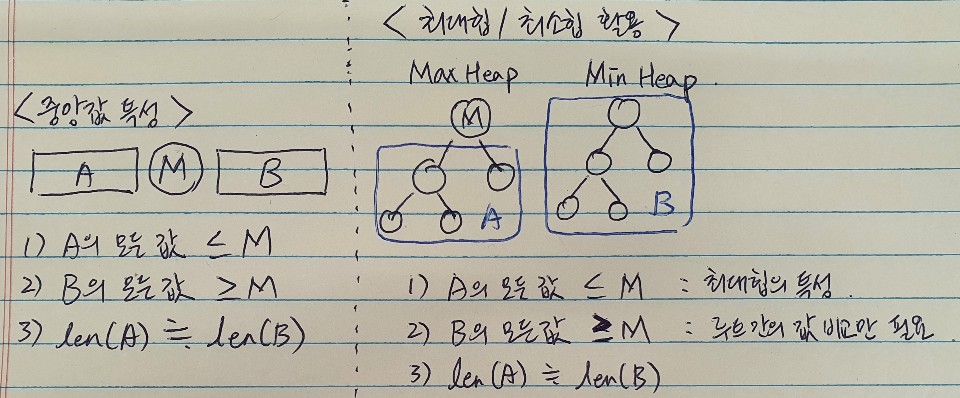
• 중앙값은 본인보다 작은 값들의 개수와 본인보다 큰 값들의 개수가 동일함

  • 전체 개수가 짝수일 때는 두 개의 중앙값 중 왼쪽 값을 중앙값으로 정함
  • 그러므로 동적 집합에서 중앙값을 찾기 위해 모든 요소들이 정렬될 필요는 없음
  • 즉, 중앙값을 기준으로 양분되는 두 개의 소집합이 아래의 조건들만 충족하면 됨
    • 소집합 A는 모든 값이 중앙값보다 작거나 같음
    • 소집합 B는 모든 값이 중앙값보다 크거나 같음
    • 소집합 A와 B는 길이가 동일함
      • 전체 집합 길이가 홀수인 경우, A와 B의 길이 동일
      • 전체 집합 길이가 짝수인 경우, A가 1 작은 것으로 정함

• 중앙값의 특성을 활용해, 최대힙과 최소힙으로 중앙값 탐색을 쉽게 만들 수 있음

  • 목표: 최대힙의 루트는 항상 전체 집합의 중앙값이 되도록 함
    • 최대힙 루트 아래의 모든 값은 최대힙 루트보다 작거나 같음
    • 최소힙 모든 값은 최대힙 루트보다 크거나 같음
    • 최대힙과 최소힙은 길이가 동일함 (최대힙이 중앙값을 포함)
      • 전체 집합 길이가 홀수인 경우, 최대힙의 길이가 1 큼
      • 전체 집합 길이가 짝수인 경우, 최대힙과 최소힙의 길이 동일

• [코드 구성]

  • 최대힙과 최소힙 생성
  • 순차적으로 입력되는 값(v)에 대하여
    • 1단계: v를 최대힙 혹은 최소힙 중 하나에 추가
      • 최대힙과 최소힙의 길이가 동일한 경우
        • 최대힙에 v 추가
          • (그 결과)
          • 최대힙에 n//2+1개, 최소힙에 n//2개의 값 존재
          • 최대힙 루트가 전체의 중앙에 위치함
          • 최대힙 루트 아래의 모든 값은 최대힙 루트보다 작거나 같음
      • 최대힙과 최소힙의 길이가 다른 경우 (즉, 최대힙의 길이가 1 큰 경우)
        • 최소힙에 v 추가
          • (그 결과)
          • 최대힙에 n//2개, 최소힙에 n//2개의 값 존재
          • 최대힙의 루트가 전체의 중앙 2개 중 왼쪽에 위치함
          • 최소힙 아래 모든 값은 최소힙 루트보다 크거나 같음
    • 2단계: 최대힙 루트와 최소힙 루트 간 비교
      • 최대힙의 루트가 최소힙의 루트보다 작거나 같은 경우
        • 최대힙의 루트를 중앙값으로 볼 수 있으므로 패스
      • 최대힙의 루트가 최소힙의 루트보다 큰 경우
        • 최대힙의 루트와 최소힙의 루트를 교환
          • (그 결과)
          • 최대힙 루트 아래 모든 값은 최대힙 루트보다 작거나 같음
          • 최소힙의 모든 값은 최대힙 루트보다 크거나 같음

제출 답안

내장된 heapq 사용한 답안

import sys
import heapq
N = int(sys.stdin.readline())

# [목표] max_h의 루트가 항상 전체 배열의 중앙값이 될 수 있도록 한다.
#   - max_h의 길이는 min_h의 길이보다 항상 1만큼 크거나 같게 유지함
#   - max_h에는 항상 max_h의 루트(중앙값)보다 작은 값들이 모여 있음
#   - min_h에는 항상 max_h의 루트(중앙값)보다 큰 값이 모여 있음
max_h, min_h = [], []
for _ in range(N):   
    v = int(sys.stdin.readline()) 
    # 1) 두 heap을 번갈아 가며 새로운 value를 추가
    if len(max_h) == len(min_h):
        heapq.heappush(max_h, (-v, v))
    else:
        heapq.heappush(min_h, (v, v))
    # 2) max_h의 루트가 min_h의 루트보다 더 크면 교환
    if min_h and max_h[0][1] > min_h[0][1]:
        lg = heapq.heappop(max_h)
        sm = heapq.heappop(min_h)
        # 주의: 부호를 반대로 변경해주어야 함
        heapq.heappush(max_h, (-sm[0], sm[1]))
        heapq.heappush(min_h, (-lg[0], lg[1]))
    
    print(max_h[0][1])

(참고) 힙을 구현한 답안

• 아래 코드는 시간 초과에 걸림
  • 통과를 위해서는 heapq 활용

def parent(i):
    return (i-1)//2

def left(i):
    return i*2+1

def right(i):
    return i*2+2

def max_heapify(arr, i):
    l, r = left(i), right(i)
    lg = i
    if l < len(arr) and arr[l] > arr[lg]:
        lg = l
    if r < len(arr) and arr[r] > arr[lg]:
        lg = r
    if lg != i:
        arr[lg], arr[i] = arr[i], arr[lg]
        max_heapify(arr, lg)

def max_extract(heap):
    L = len(heap)
    if L < 1:
        return False
    max_value = heap[0]
    heap[0] = heap[L-1]
    heap.pop()
    max_heapify(heap, 0)
    return max_value

def max_insert(heap, v):
    heap.append(v)
    i = len(heap) - 1
    while i > 0: # i == 0 이면 root
        p = parent(i)
        if heap[p] >= heap[i]:
            break
        heap[p], heap[i] = heap[i], heap[p]
        i = p
        
        
def min_heapify(arr, i):
    l, r = left(i), right(i)
    sm = i
    if l < len(arr) and arr[l] < arr[sm]:
        sm = l
    if r < len(arr) and arr[r] < arr[sm]:
        sm = r
    if sm != i:
        arr[i], arr[sm] = arr[sm], arr[i]
        min_heapify(arr, sm)

def min_extract(heap):
    L = len(heap)
    if L < 1:
        return False
    min_value = heap[0]
    heap[0] = heap[L-1]
    heap.pop()
    min_heapify(heap, 0)
    return min_value

def min_insert(heap, v):
    heap.append(v)
    i = len(heap) - 1
    while i > 0:
        p = parent(i)
        if heap[p] <= heap[i]:
            break
        heap[p], heap[i] = heap[i], heap[p]
        i = p

        
import sys
N = int(sys.stdin.readline())

# [목표] max_h의 루트가 항상 전체 배열의 중앙값이 될 수 있도록 한다.
#   - max_h의 길이는 min_h의 길이보다 항상 1만큼 크거나 같게 유지함
#   - max_h에는 항상 max_h의 루트(중앙값)보다 작은 값들이 모여 있음
#   - min_h에는 항상 max_h의 루트(중앙값)보다 큰 값이 모여 있음
max_h, min_h = [], []
for _ in range(N):   
    v = int(sys.stdin.readline()) 
    # 1) 두 heap을 번갈아 가며 새로운 value를 추가
    if len(max_h) == len(min_h):
        max_insert(max_h, v)
    else:
        min_insert(min_h, v)
    # 2) max_h의 루트가 min_h의 루트보다 더 크면 교환
    if min_h and max_h[0] > min_h[0]:
        lg = max_extract(max_h)
        sm = min_extract(min_h)
        max_insert(max_h, sm)
        min_insert(min_h, lg)
    
    print(max_h[0])