백준 2805번: 나무 자르기

문제

• https://www.acmicpc.net/problem/2805
• 탐색 배열의 요소와 탐색 목표 간에 속성이 다를 때 이진 탐색 수행하기

기록 포인트

• [일반화된 접근 방법] 이 문제가 이진 탐색 과제라는 것을 어떻게 알 수 있을까?
  • 탐색 목표와 탐색 대상을 정의
  • 고려해야 하는 모든 경우의 수를 파악
  • 그 다음 각 경우의 수를 선형 탐색 방식으로 접근해 봄
    • 선형 탐색의 종료 조건을 파악!
  • 각 경우의 수가 가진 규칙성을 파악하며 더 효율적으로 탐색할 수 있는 방법 고민
  • 특히, 각 경우의 수가 선형적으로 증가 혹은 감소한다면 이진 탐색으로 접근 가능
    • 선형 탐색의 종료 조건을 참고하여 이진 탐색에서 범위를 좁히는 로직을 구성!

• 선형 탐색의 종료 조건
  • 모든 항목을 검색했을 때
  • 탐색 목표를 찾았을 때
• 이진 탐색의 종료 조건
  • 검색 범위가 더 이상 없을 때
  • 탐색 목표를 찾았을 때
• 탐색 범위(배열)의 요소와 탐색 목표 간에 속성이 다른 이진 탐색 과제!
  • 탐색할 배열의 요소들을 탐색 목표와 동일한 속성으로 변환하여 풀면 됨
  • 자세한 내용은 접근 방식 참고

접근 방식

• 접근법을 적용하면 아래와 같음

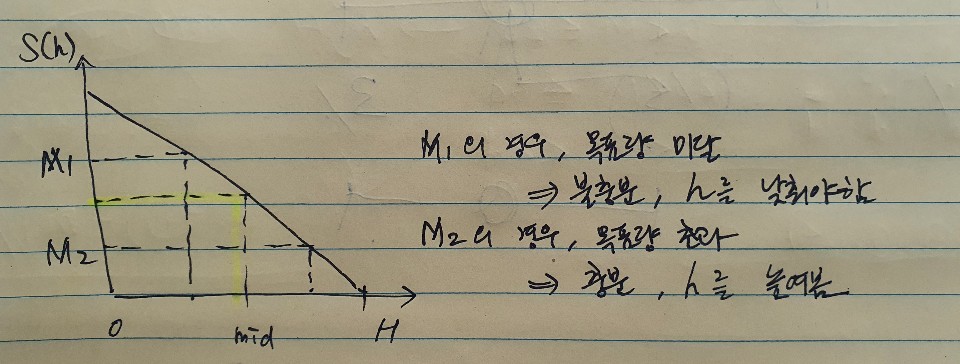
  • 탐색 목표는 목표 수확량(M)을 충족하는 절단 높이(h)의 최대값
  • 탐색 대상은 절단 높이(h)로,
  • 모든 경우의 수는 0부터 가장 큰 나무의 길이 H 사이의 값임
  • 만약 선형 탐색을 한다면 h의 최대값을 찾는 것이 목표이므로 0부터 H까지 h를 1씩 증가하며 문제를 풀고, 수확량(S)가 M보다 작은 h를 찾으면 탐색 종료
    • 즉, 선형 탐색의 종료 조건은 S(h) < M
  • h의 증감에 따라 S는 선형적으로 변화함을 확인
    • h1 < h2 이면 S1 <= S2이므로, h1이 조건 충족 실패 시 h2도 반드시 실패
    • h1 > h2 이면 S1 >= S2이므로, h1이 조건 충족 성공 시 h2도 반드시 성공
  • 이진 탐색 변형
    • 초기 설정
      • left, right 각각 0, 가장 큰 나무의 길이(H)
      • 정답의 초기값은 0 (h의 최대값을 찾는 것이므로)
    • 탐색 진행
      • 탐색 종료 시점은 탐색 범위가 더 이상 없을 때
        • left > right
      • 탐색 범위 중앙값으로 조건 충족 여부 판단
        • h는 left와 right의 평균값
        • 조건 충족은 S(h) >= M
      • 만약 특정한 절단 높이 h의 수확량 S(h)가 M과 동일하면: S(h) == M
        • h는 조건 충족이므로 최적값 업데이트
        • 탐색 종료
      • 만약 특정한 절단 높이 h의 수확량 S(h)가 M보다 크면: S(h) > M
        • h는 조건 충족이므로 최적값 업데이트
        • h보다 작은 값은 확인할 필요가 없음
      • 만약 특정한 절단 높이 h의 수확량 S(h)가 M보다 작으면: S(h) < M
        • h는 조건 미달
        • h보다 큰 값은 확인할 필요가 없음

• 절단 높이를 수확량으로 변환

  • 본 문제는 '절단 높이(h)에 따른 수확량(S)이 담긴 배열'에서 '목표 수확량(M)에 가장 근사하게 초과하는 값'을 찾는 과제임
  • 다만, 탐색할 배열의 요소인 수확량을 나무 절단 높이로 한 번 꼬아놓았음
  • 탐색하라고 주어진 배열 '절단 높이(h)'와 탐색 목표 '목표 수확량(M)'이 서로 단위가 달라 문제가 단박에 잡히지 않은 것!

• 선형 관계 파악 과정

  • 가장 큰 나무의 길이가 H라고 할 때, 절단 높이(h)는 0과 H 사이의 값임
  • 절단 높이(h)에 따라 수확량(S)가 정해지며, h가 증가함에 따라 S는 동일하거나 감소함 ( 즉, S(h) >= S(h+1) )
  • 절단 높이 0~H의 수확량은 S(0) ~ S(H)라고 할 수 있음
  • 결과적으로 우리는 S(0)과 S(H) 사이에서 M를 가장 근사하게 넘는 S(h')를 찾고 그 때의 h'를 리턴해주면 됨

• 중요 포인트 재정리

  • 탐색할 배열인 h 값들 탐색 목표 M과 단위가 달라 헷갈리지만, 사실 S(h) 값들 중에서 M을 찾는 과제임
  • 0과 H 사이의 값인 h가 S를 결정 지으며, h와 S는 선형 관계에 있음
  • 고로, S는 이진 탐색이 가능한 정렬된 배열로 볼 수 있음

제출 답안

2차 답안: 이진 탐색 활용

• 절단 높이와 수확량 간의 관계
  • 수확량을 충족하면, 해당 절단 높이를 기억해두고 더 높은 절단 높이에 도전
  • 수확량을 미달하면, 절단 높이를 낮춤
    

# 나무 높이 중복을 고려해 Counter 방식으로 나무 높이 정리
counted = {}
for tree in trees:
    if tree in counted:
        counted[tree] += 1
    else:
        counted[tree] = 1
        
# 절단 높이 값을 받아 수확량을 계산하는 함수 구현
def get_amount(h):
    total = 0
    for tree in counted:
        if tree - h > 0:
            num = counted[tree]
            total += (tree-h) * num
    return total

# 최적의 절단 높이를 이진 검색으로 탐색
# h_left: 절단 높이가 0이 되면 수확량이 가장 큰 값이 되므로 수확량 관점에서 최대 기준
# h_right: 절단 높이가 가장 큰 나무의 높이가 되면 수확량은 0이 되므로 수확량 관점에서 최소 기준
# h_answer: 절단 높이를 최대한 높이는 것이 목표이므로 0부터 시작
h_left = 0
h_right = max(counted) 
h_answer = 0  
while h_left <= h_right:
    mid = (h_left + h_right) // 2
    amount = get_amount(mid)
    # 수확량이 M 이상인 경우, 목표 달성이며 h를 더 높여봄
    if amount >= M:
        h_left = mid + 1
        h_answer = mid
    # 수확량이 M 미만인 경우, 목표 미달이며 h를 낮춰야 함
    else:
        h_right = mid - 1
        
print(h_answer)

(참고용) 1차 답안: 이진 탐색 활용 X

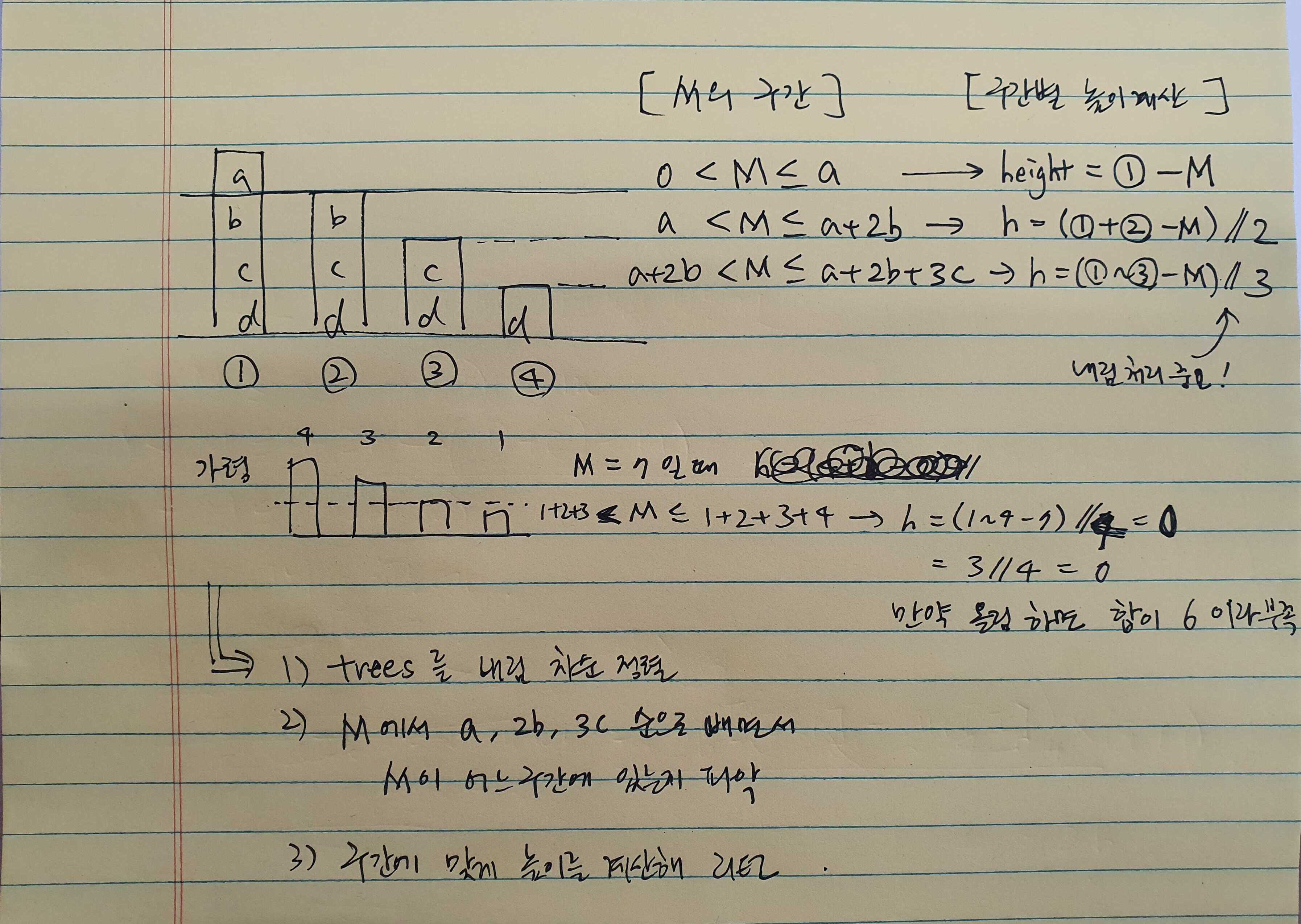
• 처음에는 이진 탐색 없이 일반화하여 풀었음
• 내용 설명은 아래 그림으로 대체
• 그런데 이 경우는 중복이 있으면 오류가 발생함! (확인 필요)
  

import sys
N, M = list(map(int, sys.stdin.readline().split()))
trees = list(map(int, sys.stdin.readline().split()))
# 나무들을 역순으로 정렬
trees.sort(reverse=True)
# 일관성을 위해 더미 아이템 추가
trees.append(0)

loc = 0
diff = M
while diff > 0:
    to_sub = (trees[loc] - trees[loc+1]) * (loc+1)
    diff -= to_sub
    loc += 1
    
height = (sum(trees[:loc]) - M) // loc
print(height)