Selection Problem

1. Names
2. Orders
3. Mathmatic

Problem 1. Finding MAX

currentMax = A[0]
for i = 1 to n-1 do
	if currentMax < A[i] # compares 
    	currentMax = A[i]
	return currentMax

This takes O(n) complexity and we cannot get faster oen since this is the lower bound(at least, we have to take a look at every elements to compare, and it takes n times...)

Problem 2. Finding MIN&MAX

Algorithm 1: Find Max, then find Min among the rest.

obviously, it takes 2n-3 times. n-1 for previous, n-2 for next calculation.

Do we have better option? Yes.

Algorithm 2: Find Max as tonamant rule, keep the losers` list which is min value exists, and get min from the list.

In this case, finding min value will be much faster as the list is only n/2 size. Overall, we need

$(n-1) + (\frac{n}{2}-1) = \frac{3}{2}n - 2$

Problem 3. Finding Min and SECOND Min

Remember: second smallest value must match with the smallest. BUT we cannot sure that the match is the final one. That means, the second min will be in somewhere of group of elements matched with the smallest. IF we can save the group, we can confine the candidates in a very small area.

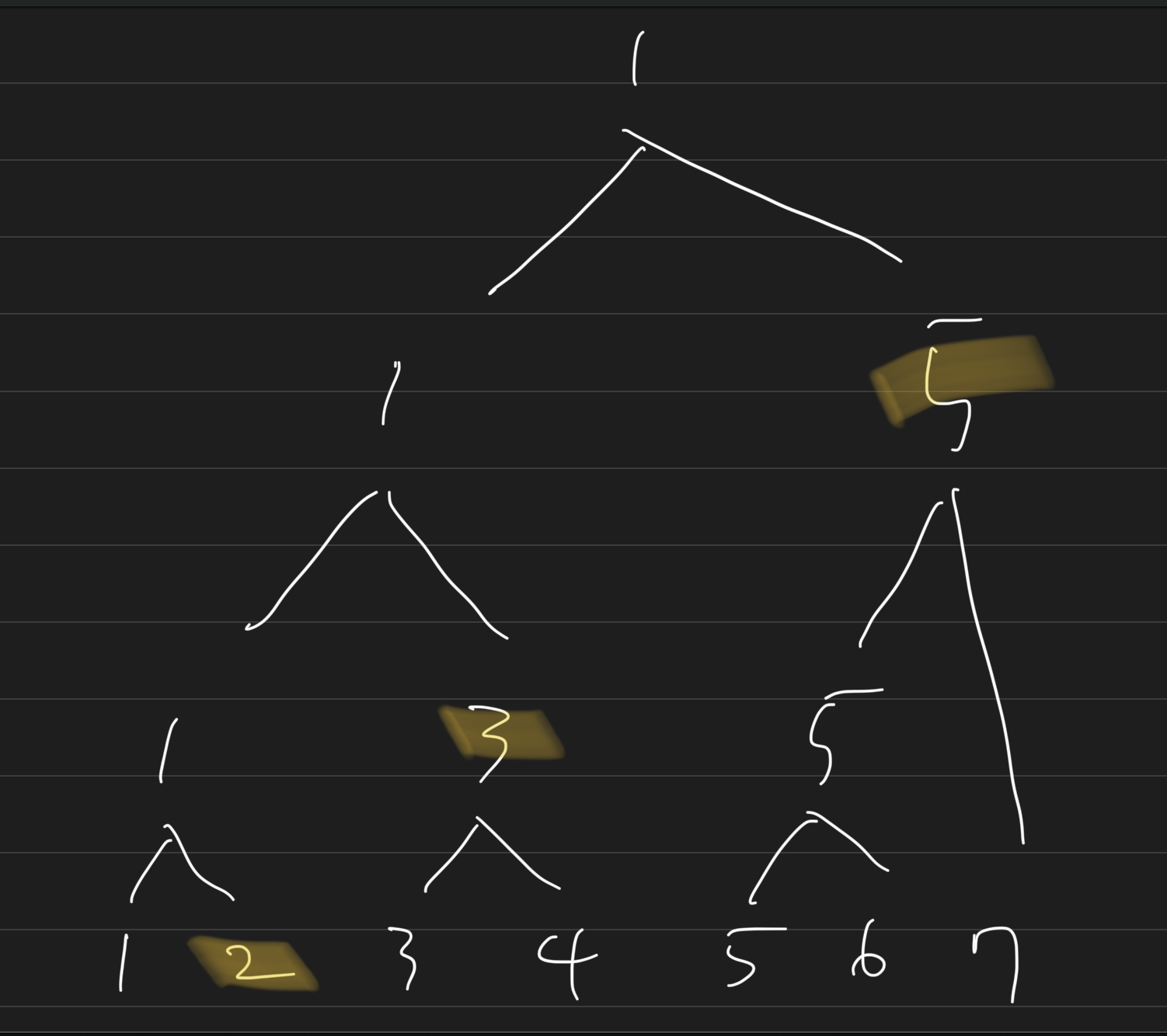
Size of THE GROUP is 3, and it's equal as upper bound of $\lceil log_27 \rceil=8$

In conclusion, we can find min within

$n-1 + log_2{n}-1$

Problem 4. Finding k-th smaller value

a.
if k = 1, it's same as finding min
if k= n, it's same as finding max
if k = n/2, it's finding median

b.
Idea: to reduce the candidates group

1. Size of the candidates group is n at first.
2. Reduce the size into n/2 and process.
3. Reduce the size itno n/4 and process.
4. Repeat this.