문제 링크
문제분류 : DP
난이도 : Medium
결과: 실패

문제 설명

2*n 사각형을 1*1, 1*2, 2*1 크기의 사각형들로 채우는 경우를 구하는 DP 문제

나의 풀이

알아보기 힘들지만, 이렇게 네 가지 경우로 끝나는 케이스가 있다고 생각했다. 그래서 1 by 1 블럭으로 끝나는 경우 둘과 나머지 두 경우를 따로 묶어서 별도의 dp식을 만들고 그것을 합산한 것이 정답이 아닐까 생각했지만,

A[i] = A[i] + A[i-1]
B[i] = 2 * B[i-1]
DP[i] = A[i] + B[i]

당연히 아닐 거 같은 삘이 강하게 들었다.

결론은 당연히 아니었고, 이 문제를 풀기 위해서는 i-1, i-2, i-3, i-4...i-i 까지 채우는 모든 방법을 고려한 다음 점화식을 도출해내야 한다. 중요한 것은,

1. dp에서 한 '방법'은 다른 '방법'과 완전히 독립적이어야 한다
2. i-k에서 k가 무엇이 되었든 그 이전의 사건들은 해결이 되었다고 가정하고, 그 상황에서 i를 해결할 수 있는 경우의 수를 곱하든 더하든 비교하든 해서 dp[i]를 정의해야 한다. (이게 dp의 핵심 사고방식인데, 잘 적용이 안 된다.)

이 점을 잘 고려하지 못하면 dp가 서로 종속적인 사건들의 경우의 수로 채워지게 되고, 이상하게 큰 값을 얻는 결과로 이어진다.

솔루션

그래서 이것을 다시 생각해서 점화식을 계산해보면...
dp[i-1]: i-1까지 채워졌다고 생각할 때 남은 칸을 채울 수 있는 경우의 수
dp[i-2]: i-2까지 채워졌다고 생각할 때 남은 칸을 채울 수 있는, 위의 경우에서 독립된 경우의 수.

이런식으로 가정할 때
dp[i-1]
dp[i-2]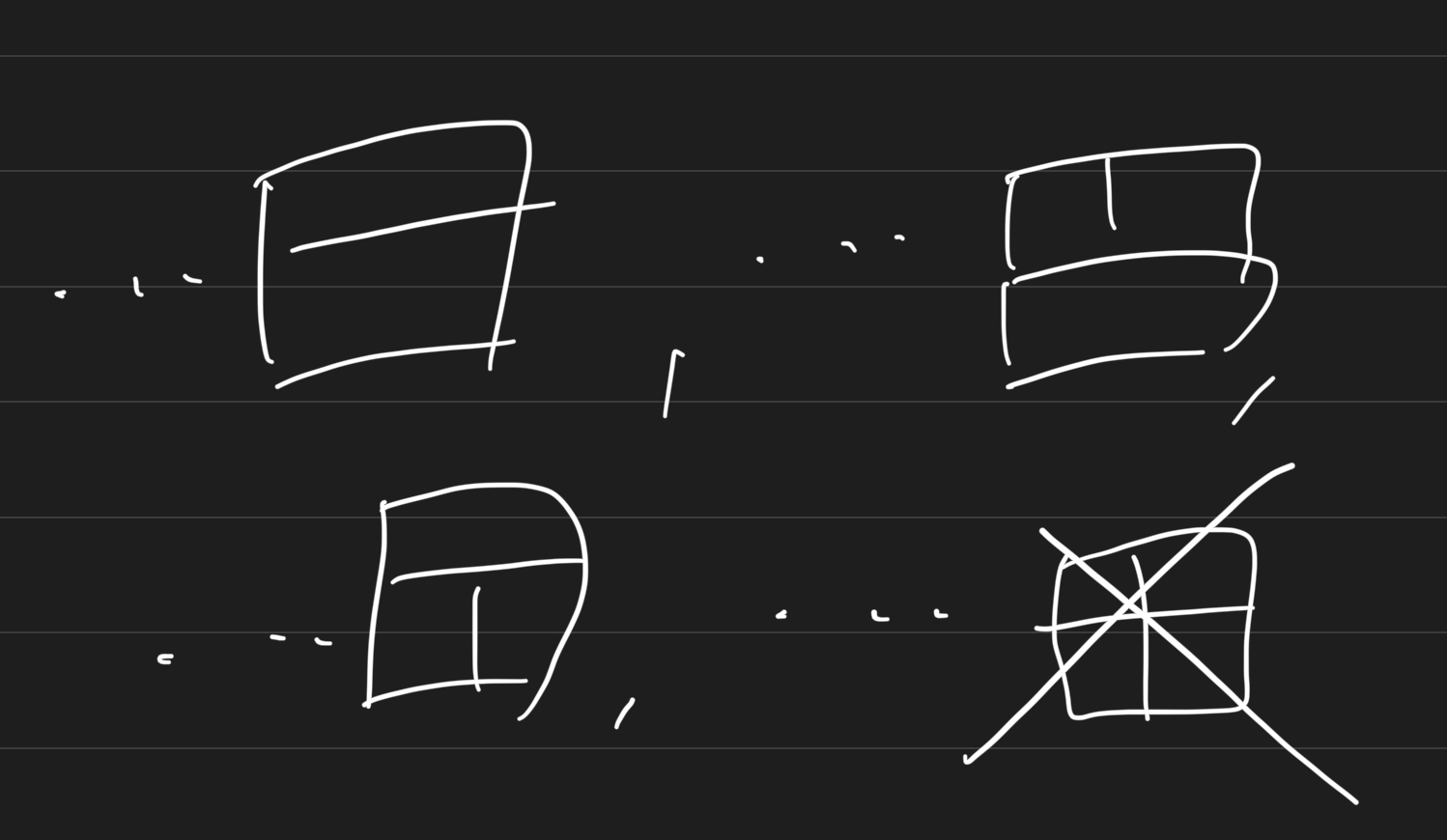
dp[i-3]
dp[i-4]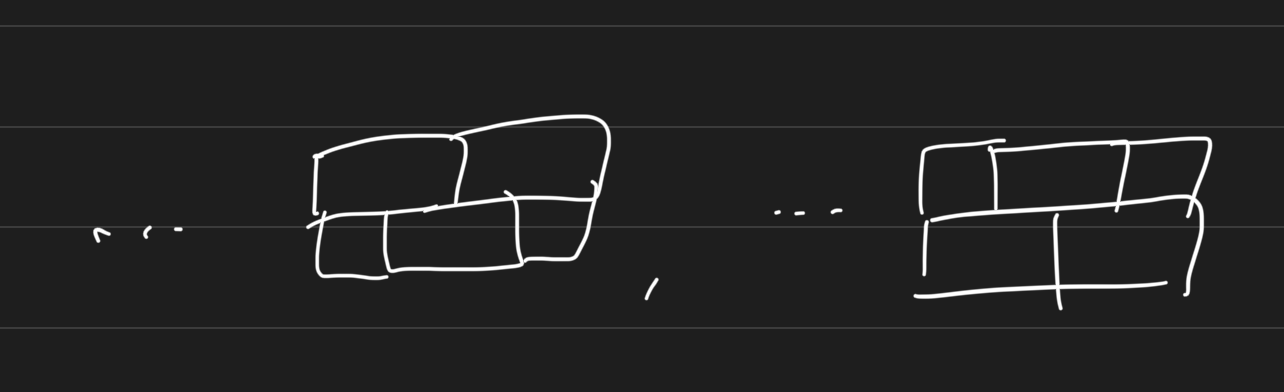

이런 모습으로, 직관적으로 채워야 하는 칸이 3칸이 넘어갈 경우 전부 2가지 경우만 가능함을 알 수 있다.

dp식 초기화 단서도 이미 나왔으니 그대로 코딩만 하면 된다.

그럼에도 불구하고, 제대로 풀지 못했다. 문제가 뭐였냐면, dp[0]을 제대로 정의하지 못했기 때문이다. dp[0]을 1로 정의할지 0으로 정의할지 혹은 다른 무엇으로 정의할지는 문제의 '정의'에 따라서 달라지는 아주 중요한 문제다.
방법의 수를 구하는 경우는 dp[0]을 아무것도 하지 않아도 그 방법 자체로 이미 해결된 상태, 즉 1로 보고, 냅색 문제 같은 경우는 선택을 하지 않아서 가치가 0인 걸 의미해서 dp[0]=0이어야 한다.

따라서 이번 경우, dp[0]은 그 자체로 이미 문제가 해결된 경우 하나로, 1로 초기화하고, dp[1]은 2로 초기화 한다. dp[2]부터는 $dp[2] = 2*dp[1] + 3*dp[0] + (나머지\ 이터레이션\ 파트는\ 이\ 경우\ 불필요)$ 이렇게 채우면 되므로 문제 정의상 초기화하지 않아도 된다.

따라서 초기화 및 dp 작성 코드는 다음과 같다.(모듈러 연산은 무시해도 무방)

		dp[0] = 1;
        dp[1] = 2;
        for(int i = 2; i <= n; i++){
            int tmp = 0;
            for(int j = 0; j < i-2; j++){
                tmp += (2*dp[j])%1000000007;
            }
            dp[i] = (2*dp[i-1]+3*dp[i-2]+tmp)%1000000007;
        }