알고리즘 평가법

guava·2021년 9월 18일

알고리즘 코드잇

알고리즘의 정석

목록 보기

4/13

코드잇의 알고리즘의 정석 수업을 수강하고 정리한 글입니다.
정확하지 않거나 빠트린 내용이 있을 수 있기 때문에 강의를 수강하시길 권장합니다.

1. 평가의 기준: 시간과 공간

시간: 우리는 빨리 작업이 수행되기를 원한다.
공간: 컴퓨터의 저장 공간 (메모리를 적게 사용해야 좋은 프로그램)

메모리는 어느정도 비용으로 극복 가능한 부분이 있지만 시간은 그렇지 않기 때문에 두 평가의 기준 중 시간을 더 중요한 가치로 둔다.

2. 시간복잡도

데이터가 많아질수록 걸리는 시간이 얼마나 급격히 증가하는가

인풋 크기	알고리즘 A	알고리즘 B
10개	10초	10초
20개	20초	40초
100개	100초	1000초

표 1. 알고리즘 별 시간복잡도

알고리즘 A는? 시간 복잡도가 작다 → 더 빠른 알고리즘
알고리즘 B는? 시간 복잡도가 크다 → 더 느린 알고리즘

3. 거듭제곱과 로그

거듭제곱 (Exponentiation)

23 = $2\times2\times2$ = 8

22 = $\frac{2^3}{2}$ = $\frac{8}{2}$ = 4

$2^1$ = $\frac{2^2}{2}$ = $\frac{4}{2}$ = 2

$2^0$ = $\frac{2^1}{2}$ = $\frac{2}{2}$ = 1

2-1 = $\frac{2^0}{2}$ = $\frac{1}{2}$

로그 (Logarithms)

$\log{_a}{b} = x$ $\rightarrow$ $a^x = b$

a에 몇을 곱해야 b가 나올까??

즉, b를 a로 몇번 나누어야 1이 되는가?

컴퓨터 알고리즘에서는 a=2인 경우가 많다. 이럴 때는 "b를 몇번 반토막 내야 1이 나오는가?"로 생각해 볼 수 있다.

$log{_2}{8} = 3 \rightarrow 2^3=8$
$log{_3}{27} = 3 \rightarrow 3^3 = 27$

8을 2로 3번 나누어야 1이 되며 27을 3으로 3번 나누어야 1이 된다.

또한 $a=2$ 인 경우에는 $\log{_a}{n}$ 을 $\lg{n}$ 으로 쓰기도 한다.

4. 1부터 n까지의 합

  T = 1 +  2    +   3   + ... + (n-2) + (n-1) + n
+ T = n + (n-1) + (n-2) + ... +   3   + 2    +  1
--------------------------------------------------
 2T=(n+1) (n+1) (n+1)           (n+1)  (n+1)  (n+1)

2T = n*(n+1)
T =  n*(n+1)/2   # 1부터 n까지의 합

5. 점근 표기법 (Big-O Notation)

리스트의 길이 n

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53]

알고리즘의 소요 시간

$20n + 40$
$2n^2 + 8n + 157$
$20\lg{n} + 60$

숫자들은 컴퓨터의 성능이나 프로그래밍 언어 등의 환경적인 요소에 따라 달라진다. (수식만으로는 알고리즘의 소요 시간을 완벽하게 표현할 수 없다.)
따라서, 컴퓨터 과학자들은 알고리즘을 평가는 방법으로 "점근 표기법"을 제시하였다.

소요시간	점근표기법(Big-O)
$20n+40$	$O(n)$
$2n^2+8n+157$	$O(n^2)$
$5n^3+100n^2+75$	$O(n^3)$
$20\lg{n}+60$	$O(\lg{n})$

표2. 점근 표기법의 예

점근 표기법의 핵심

n의 영향력이 가장 큰 곳을 찾고 나머지는 삭제
n앞에 붙은 숫자를 삭제해준다.

왜 점근표기법을 사용할까?

우리의 관심사는 절대적인 시간이 아닌 성장성이다.

점근 표기법의 핵심은 n이 크다고 가정하는 것이다.

→ n이 크지 않으면 안 좋은 알고리즘을 써도 문제 없다.

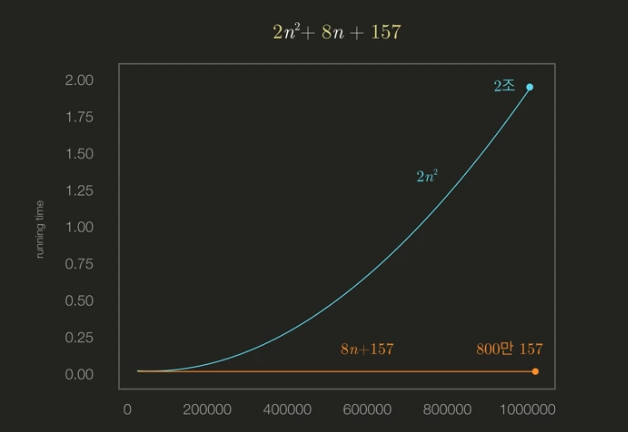
$2n^2 + 8n + 157$ 과 $8n + 157$ 을 비교한 그래프이다.

input size(이하 n)이 커질 수록 그래프 기울기 차이가 많이나며, n=1000000일 때에는 각각 2조, 8백만의 시간값(세로축)을 갖는다. 아래 그림과 같이 $8n + 157$ 이 아닌 $8000n + 157$ 과 비교한다고 하더라도 n이 커질 수록 격차가 급격하게 벌어진다. 이는 중요한 영향을 주는 2n^2이외에는 무시해도 된다는 결론에 도달할 수 있다.

이로 인해 n의 영향력이 가장 큰 곳( $2n^2 + 8n + 157$ 에서 $2n^2$ )을 찾고 나머지는 삭제한다는 첫번째 핵심이 도출된다.

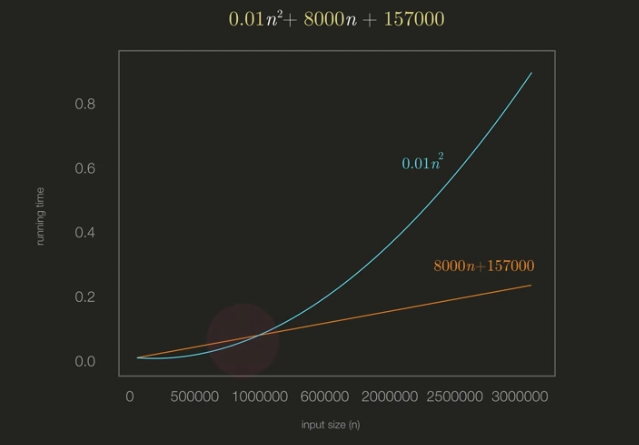
$2n^2 + 8n + 157 \rightarrow 0.01n^2 + 8n + 157$ 로 수정 후 비교하더라도, 파란 직선이 주황 직선의 추월할 시기가 달라질 뿐이다. 결국은 $n^2$ 이라는 점이 중요하므로 "n앞에 붙은 숫자를 삭제해준다."라는 두번째 핵심이 도출된다.

6. 점근 표기법의 의미

O(1), O(n), O(n^2), O(n^3)의 속도를 갖는 4개의 알고리즘을 비교해보자.

n (예: 인풋 리스트의 길이)	$O(1)$ 알고리즘 소요 시간	$O(n)$ 알고리즘 소요 시간	$O(n^2)$ 알고리즘 소요 시간	$O(n^3)$ 알고리즘 소요 시간
100	1초	1초	1초	1초
200	1초	2초	4초	8초
1000	1초	10초	100초	1000초
10000	1초	100초	10000초	1000000초

표3. 알고리즘 비교

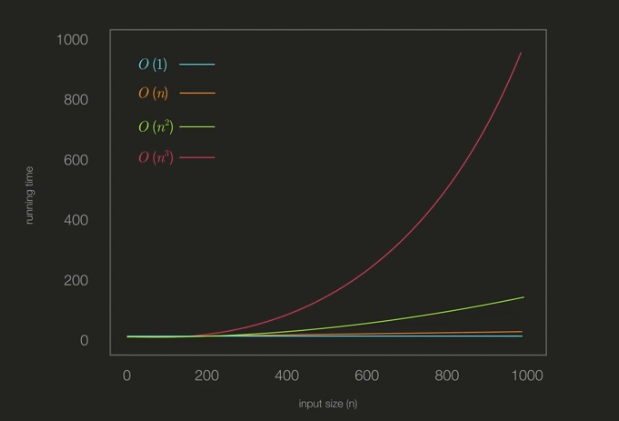
환경이 다를 때 알고리즘 비교

다른환경에서 실행한다고 하더라도 알고리즘이 좋지 않으면 결국 많은 소요시간을 갖는다는 점을 알 수 있다.

n (예: 인풋 리스트의 길이)	$O(1)$ 알고리즘 소요 시간	$O(n)$ 알고리즘 소요 시간	$O(n^2)$ 알고리즘 소요 시간	$O(n^3)$ 알고리즘 소요 시간
100	10초	1초	0.1초	0.01초
200	10초	2초	0.4초	0.08초
1000	10초	10초	10초	10초
10000	10초	100초	1000초	10000초

표4. 환경이 다를 때 알고리즘 비교

7. 탐색 알고리즘 평가하기

# 선형탐색 평가하기
def linear_search(element, some_list):
    i = 0  # O(1)
    n = len(some_list) # O(1)

    while i < n:  # O(1) x 반복횟수(n)
        if some_list[i] == element:
            return i
        i += 1

    return -1  # O(1)

최고의 경우 : $O(1) + O(1) + O(1) + O(1) = O(4) = O(1)$
최악의 경우 : $O(1) + O(1) + O(n) + O(1) = O(n + 3) = O(n)$

def binary_serach(element, some_list):
    start_index = 0  # O(1)
    end_index = len(some_list -1) # O(1)

    while start_index <= end_index:  # O(1) x 반복 횟수 (lg n)
        midpoint = (start_index + end_index) // 2
        if some_list[midpoint] == element:
            return midpoint
        elif element < some_list[mid_point]:
            end_index = midpoint - 1
        else:
            start_index = midpoint + 1

    return None  # (1)

최고의 경우 : $O(1) + O(1) + O(1) + O(1) = O(4) = O(1)$
최악의 경우 : $O(1) + O(1) + O(\lg{n}) + O(1) = O(\lg{n} + 3) = O(\lg{n})$

8. 알고리즘 평가 주의 사항

점근 표기법에서 n은?

인풋 크기를 나타낼 때 흔히 사용되는 문자로서 별다른 의미는 없으며, 다른 문자로 표현해도 무방하다.

코드의 모든 줄은 O(1)일까?

인풋 크기와 실행 없이 실행되는 코드만 O(1)이다.

Operation	Code	Avarage Case
인덱싱	my_list[index]	O(1)
정렬	my_list.sort() sorted(my_list)	O(nlgn)
뒤집기	my_list.reverse()	O(n)
탐색	element in my_list	O(n)
끝에 요소 추가	my_list.append(element)	O(n)
중간에 요소 추가	my_list.insert(index, element)	O(n)
삭제	del my_list[index]	O(n)
최솟값, 최댓값 찾기	min(my_list) max(my_list)	O(n)
길이 구하기	len(my_list)	O(1)
슬라이싱	my_list[a:b]	O(b-a)

표5. List Operations

Operation	Code	Avarage Case
값 찾기	my_dict[key]	O(1)
값 넣어주기/덮어쓰기	my_dict[key] = value	O(1)
값 삭제	del my_dict[key]	O(1)

표6. Dictionary Operation

9. 주요 시간 복잡도 총정리

시간 복잡도(Time Complexity)는 인풋 크기에 비례하는 알고리즘의 실행 시간을 나타낸다.

$O(1)$ : 인풋의 크기가 소요 시간에 영향이 없다.

$O(n)$ : 반복문이 있고, 반복되는 횟수가 인풋의 크기와 비례하면 일반적으로 $O(n)$ 이다. 반복문의 개수에 따라 $O(3n)$ 등이 될 수 있으나 결론적으로 3은 버려져서 $O(n)$ 이 된다고 볼 수도 있다.

$O(n^2)$ : 반복문이 중첩되었을 경우 (반복문 안에 반복문)

$O(n^3)$ : 반복문이 세번 중첩되었을 경우

$O(\lg{n})$ : 반복이 수행될 때마다 단계가 줄어든다.

# case 1
# O(lg n) 함수
# 2의 거듭제곱을 출력하는 함수
# (이번에는 인풋이 리스트가 아니라 그냥 정수입니다)
def print_powers_of_two(n): # n = 128일 때
    i = 1
    while i < n: # i=1, 2, 4, 8, 15, 32, 64까지 7회 실행된다.
        print(i)
        i = i * 2  # i의 값이 2배 씩 증가한다. 이 코드가 수행될 때마다 필요한 수행 단계가 줄어든다.

# case 2
# O(lg n) 함수
# 2의 거듭제곱을 출력하는 함수
# (이번에는 인풋이 리스트가 아니라 그냥 정수입니다)
def print_powers_of_two(n): # n = 128일 때
    i = n
    while i > 1: # i=128, 64, 32, 16, 8, 4, 2까지 7회 실행된다.
        print(i)
        i = i / 2  # i의 값이 반씩 나눠진다. 마찬가지로 필요한 수행단계가 줄어든다.

$O(n\lg{n})$ : $O(n)$ 과 $O(\lg{n})$ 이 중첩된다.

def print_powers_of_two_repeatedly(n):
    for i in range(n): # 반복횟수: n에 비례
        j = 1
        while j < n: # 반복횟수: lg n에 비례
            print(i, j)
            j = j * 2

10. 코드가 있어야만 평가할 수 있나요?

코드없이 알고리즘을 평가하는 팁

간단한 알고리즘 중 하나인 선형 탐색을 생각해보자. 대략적으로 반복횟수가 최악의 경우 $n$ 이라는 점을 생각해 볼 수 있다. 그리고 이진탐색의 경우에는 리스트를 반씩 잘라내니까 최악의 경우에 $\log{_2}{n}$ 을 떠올릴 수 있다. 그러면 다음과 같이 생각해 볼 수도 있을 것이다.

"선형 탐색을 하려면 최악의 경우에 n개를 봐야하니까 $O(n)$ 이겠구나~"
"이진 탐색을 하려면 최악의 경우이 $\log{_2}{n}$ 개를 봐야하니까 $\lg{n}$ , 즉 $O(\lg{n})$ 이겠구나~"

빅오 표기법 자체가 대충, 혹은 대략적으로 알고리즘의 성능을 평가하기 위한 목적으로 만들어졌다는 점을 명심하자.
내부적인 동작이 머리로 그려지면 이런식으로 대충 시간복잡도를 떠올릴 수 있다. 머리로 계산하는 연습을 꾸준히 하자.

11. 공간 복잡도

공간 복잡도(Space Complexity)는 인풋 크기에 비례해서 알고리즘이 사용하는 메모리 공간을 의미한다.

def product(a, b, c):
    """result의 공간은 인풋과 무관하기 때문에 공간 복잡도는 O(1)"""
    result = a * b * c
    return result

def get_every_other(my_list):
   """인풋인 my_list의 크기는 every_other의 공간에 영향을 준다. O(n/2) -> O(n)"""
    every_other = my_list[::2]
    return every_other

def largest_product(my_list):
    """인풋인 my_list의 크기는 중첩된 반복문에 의해 products의 공간에 영향을 준다. O(n^2)"""
    products = []
    for a in my_list:
        for b in my_list:
            products.append(a * b)
    
    return max(products)