자료구조 - 힙 heap (Java)

제훈·2024년 7월 13일

Java 자료구조

자료구조

목록 보기

3/4

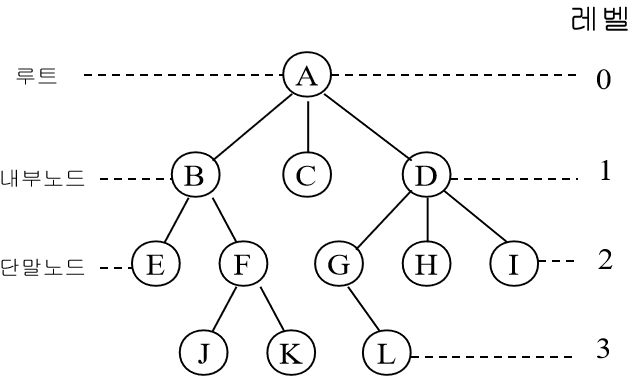
Heap

Heap (힙) : 최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전 이진 트리 형태로 만들어진 자료구조

트리

간단하게 트리부터 알고 가자

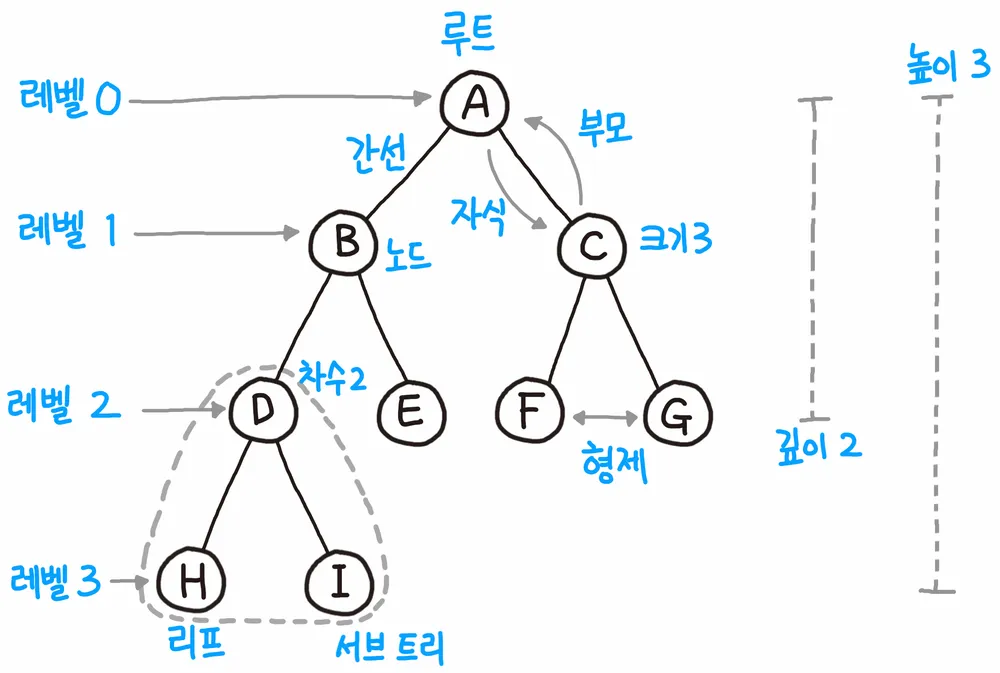
루트 노드 (root node) : 일명 뿌리 노드라고 하며 루트 노드는 하나의 트리에선 하나밖에 존재하지 않고, 부모노드가 없다. (이미지 상 A)
부모 노드(parent node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 높은 노드를 의미 (ex. C의 부모노드 : A)
자식 노드(child node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 낮은 노드를 의미 (ex. A의 자식노드 : C)
단말 노드(leaf node) : 리프 노드라고도 불리며 자식 노드가 없는 노드를 의미한다. (이미지에서 H, I, E, F, G)
내부 노드(internal node) : 단말 노드가 아닌 노드
형제 노드(sibling node) : 부모가 같은 노드를 말한다. (ex. F, G는 모두 부모노드가 C이므로 F, G는 형제노드다.)
깊이(depth) : 특정 노드에 도달하기 위해 거쳐가야 하는 '간선의 개수'를 의미 (ex. E의 깊이 : A→B→E 이므로 깊이는 2가 됨)
레벨(level) : 특정 깊이에 있는 노드들의 집합을 말하며, 구현하는 사람에 따라 0 또는 1부터 시작한다.
차수(degree) : 특정 노드가 하위(자식) 노드와 연결 된 개수 (ex. B의 차수 = 2 {D, E} )

부모 노드는 항상 자식 노드보다 우선순위가 높다.

이진 트리

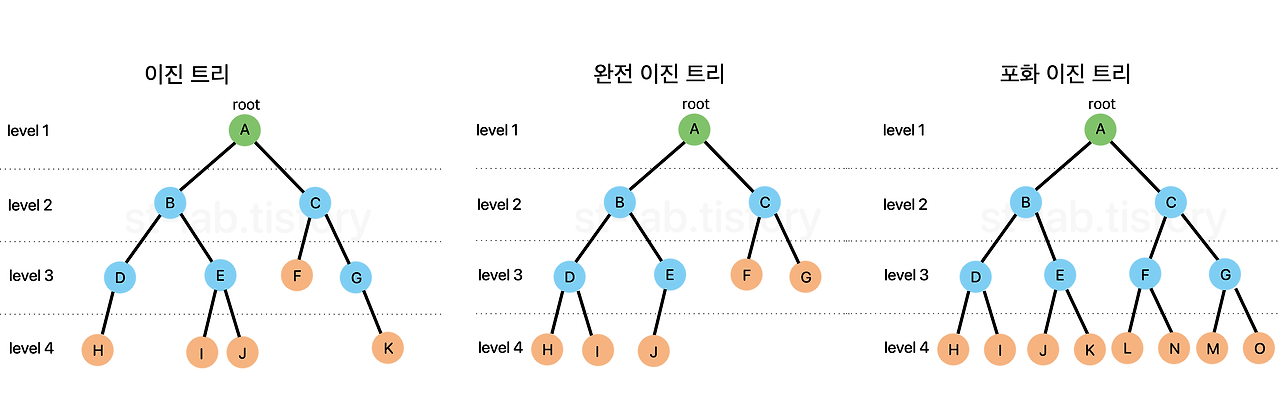
모든 노드의 최대 차수를 2로 제한한 것이다.

위의 이미지는 한 부모 노드의 자식 노드는 2개씩 연결돼 최대 차수가 2인 이진 트리이다.

완전 이진 트리

마지막 레벨을 제외한 모든 노드가 채워져 있어야 한다.
모든 노드는 왼쪽부터 채워져 있어야 한다.

2가지 조건이 충족돼야 한다.

(포화 이진 트리 : 마지막 레벨을 제외한 모든 노드가 2개의 자식노드를 가져야 한다.)

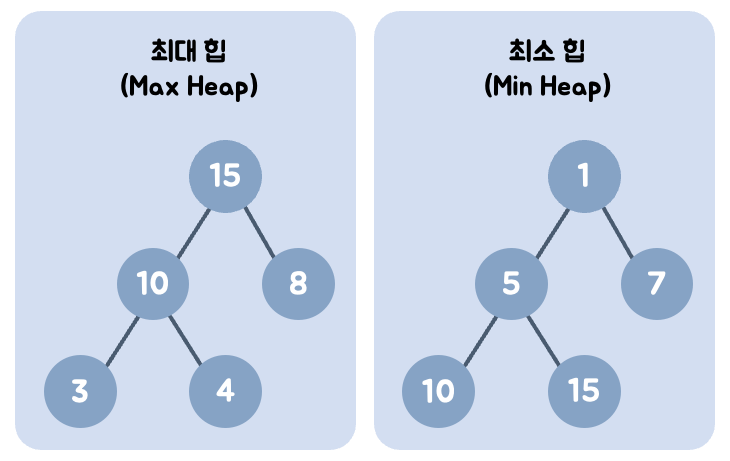
Heap 종류

최소 힙

최대 힙

최소 힙

부모 노드 값이 자식 노드의 값보다 작거나 같다.
루트 값은 저장된 원소 중 가장 작다.

최대 힙

부모 노드 값이 자식 노드의 값보다 크거나 같다.
루트 값은 저장된 원소 중 가장 크다.

장단점

장점

빠른 삽입 및 삭제 : Heap은 특정한 순서에 따라 정렬된 상태를 유지한다.
삽입과 삭제 시간이 ( O(log n) )에 이뤄진다.
우선순위 기반 작업 처리 : Heap은 우선순위 큐와 같은 다른 추상 자료형을 구현하는데 사용된다.

최대 힙의 경우) 가장 큰 우선순위를 가진 요소에 빠르게 접근 가능
최소 힙의 경우) 가장 작은 우선순위를 가진 요소에 빠르게 접근 가능

단점

임의 접근의 어려움 : Heap은 완전 이진 트리의 형태로, 배열 or 연결 리스트를 사용해 구현한다. 특정 요소를 찾는데에는 ( O(n) ) 시간이 걸린다.
정렬 유지의 오버헤드 : Heap은 정렬된 상태를 유지하기 위해 삽입과 삭제 연산 시에 정렬을 조정해야 한다. -> 오버헤드를 발생시킬 수 있다.
배열로 구현 시 추가적 공간 요구 : 배열 기반의 Heap은 공간을 미리 할당해야 하므로 요소의 개수에 따라 추가적인 공간을 필요로 한다.

최소 Heap 구현

이는 PriorityQueue로 만든 것과 같다.

import java.util.PriorityQueue;
import java.util.Queue;

public class QueueApplication {
    public static void main(String[] args) {
        Queue queue = new PriorityQueue();

        queue.offer(500);
        queue.offer(35);
        queue.offer(77);
        queue.offer(1);

        System.out.println(queue);

        // 최소값 확인
        int minValue = minHeap.peek();
        System.out.println("Min value: " + minValue); // Min value: 1

        // 최소값 삭제
        int deletedValue = minHeap.poll();
        System.out.println("Deleted value: " + deletedValue); // Deleted value: 1

        // 최소값 확인
        minValue = minHeap.peek();
        System.out.println("Min value: " + minValue); // Min value: 2
    }
}