[논문 리뷰]Structured Denoising Diffusion Models in Discrete State-Spaces

논문링크

notion에서 작성하고 옮겨서 보기 불편할 수 있다.

Abstract

DDPM은 continual state space에서 이미지, waveform 생성에 눈에 띄는 성과를 보임.

이 논문은 Discrete Denoising Diffusion Probabilistic Models(D3PMs)를 제시

이는 이전에 uniform transition probability discrete diffusion model을 generalize하는 discrete data 생성 모델

Introduction

최근 diffusion model이 뛰어난 성능을 보이고 활발하게 연구가 이루어지는데 최근 연구들은 gaussian diffusion process에 집중이 되어있고 discsrete에 대해 연구가 이루어지긴 했지만 large scale text, image generation에서 뛰어난 성능을 보여주지 못하였다.

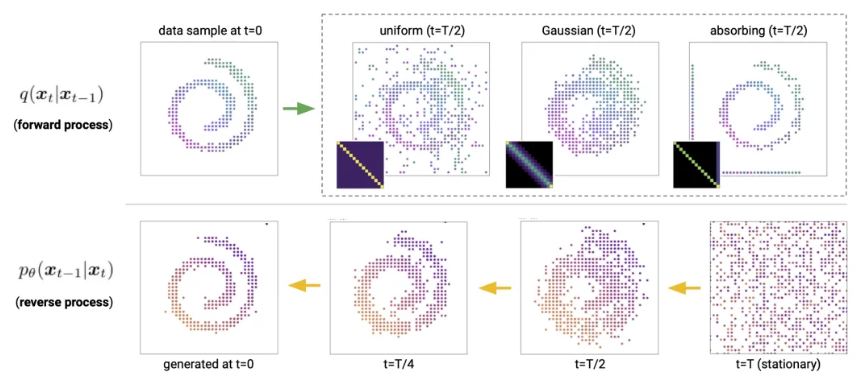
이 논문의 contribution

• discrete diffusion을 structured categorical corruption process를 통해서 discrete diffusion model을 improve하는 것을 제시. 이때 dicrete data를 continuous에 mapping을 하지 않아도 가능하고 domain knowledge를 transition matrix에 넣을 수 있다.
• loss에서 보조 loss를 추가하고 noise scheduling을 넣어서 성능을 향승시켰다.

3 Diffusion models for discrete state spaces

diffusion의 ELBO는 다음과 같다.

$-\log p_\theta(x_0)\le \mathbb E_{q(x_{1:T}|x_0)}[D_{KL}(q(x_T|x_0)||p(x_T))+\sum_{i>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))-\log p_\theta(x_0|x_1)]$

위 식을 바탕으로 diffusion의 효율적인 학습을 위해서 중요한 것

• 임의의 t에 대해서 $q(x_t|x_0)$를 바로 구할 수 있으면 $L_{t-1}$를 임의로 추출해서 gradient descent로 바로 학습이 가능.
• $q(x_{t-1}|x_t,x_0)$가 tractable 해야 KL을 구할 수 있다.

ddpm에서는 $q(x_t|x_{t-1})=\mathcal N(x_t|\sqrt{1-\beta_t}x_{t-1},\beta_tI)$, $p_\theta(x_{t-1}|x_t)=\mathcal N(x_{t-1}|\mu_\theta(x_t,t),\sum_\theta(x_t,t))$로 구하였다.

이때 $t \rightarrow\infin$으로 갈때 $q(x_t|x_0)$가 stationary distibution으로 가는 것이 중요하다. ddpm에서는 가우시간 noise $\mathcal N(0,I)$로 진행

앞의 필요한 것들을 D3PM에 대해서 정리

d3pm은 categorical one-hot vector $x=[0,0,1]$과 같이 주어졌을때
$[0,0,1]\times \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}$ 와 같이 진행이 된다. $a_{ij}$는 i번째 categorical에서 j번째 categorical로 transition될 확률이다.

즉 matrix를 Q라고 할때 $q(x_t|x_{t-1})=\text{Cat}(x_t;p=x_{t-1}Q_t)$로 표현이 된다.

• 추가로 이때 $q(x_t|x_{t-1})$의 확률에서 $x_t$가 주어졌을 때 확률을 구하면 $x_{t-1}Q_tx_t^\top$이다. 즉 $x_t$가 one-hot이기 때문에 그 1인 one-hot이 나올 확률을 구하는 것.
• $q(x_t|x_0)$: $q(x_t|x_0)=\text{Cat}(x_t;p=x_0\bar Q_t) \quad \text{with}\quad \bar Q_t=Q_1Q_2...Q_t$ 이다.
• $q(x_{t-1}|x_t,x_0)$: $q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}=\text{Cat}(x_{t-1};p=\frac{x_tQ^\top_t \cdot x_0\bar Q_{t-1}}{x_0\bar Q_tx^\top_t})$이다.
  왜 이렇게 나오면 확률에 대해서 잘 생각해야 하는 게 현재 우리는 $x_t,x_0$은 주어져있는 상황에서 $x_{t-1}$의 분포를 알고 싶은 것이다.
  나머지 $q(x_{t-1}|x_0)$나 $q(x_t|x_0)$는 tirivial한데 조금의 차이가 있다. $q(x_t|x_0)$는 $x_t$가 주어졌기 때문에 정확한 확률을 구할 수 있는데 이는 $x_t\bar Q_tx_t^\top$이다.
  $q(x_t|x_{t-1},x_0)$는 조금 복잡하다. $q(x_t|x_{t-1})$로 바꿀 수 있기에 $x_{t-1}Q_tx_t^\top$으로 표현할 수 있지만 현재 $x_{t-1}$의 분포를 모르고 우리는 구하고 싶은 것이다. 그렇게 $x_{t-1}$의 가능한 모든 분포를 다 넣으면 $I$로 표현이 가능한데
  $q(x_t|x_{t-1})=IQ_tx_t^\top=Q_tx_t^\top$이 되고 이렇게 해서 나온 $k \times 1$의 분포가 각 one-hot encoding $x_{t-1}$의 모든 값에 대한 $x_t$의 확률이다. 이를 element wise 곱해주면 $q(x_{t-1}|x_t,x_0)$의 분포가 된다.

만약 Q에서 K나 T가 매우 클 때 어떻게 처리하지?

Q는 (KxK) matrix이고 $\bar Q_t$를 저장하기 위해서 O(KxKxT)의 공간이 필요하다. 이때 K나 T가 매우 크면 어떻게 저장할까?

• low rank corruption $Q_t=\beta_tA_t+(1-\beta_t)I$로 구성한다. 이때 A는 row-rank matrix. $\beta$의 확률로 $A$를 통해서 가고 아니면 $I$로 진행하는 의미 이때 $rank(A)=r$이면 $A=UK$에서 $N\times r, r\times N$으로 나눌 수 있기에 저장하기 쉽다.
  • uniform 분포의 경우: $A={1 1^\top}/K$라고 할 때 $AA=A$를 만족시킨다.
    그렇기 때문에 $\prod_i[(1-\beta_t)I+\beta_tA]$를 polynomial하게 계산할 수 있어서 빠르게 할 수있다.
    ex) 2번 곱해지면 $(1-\beta_t)^2I+[2*(1-\beta_t)\beta_t+\beta_t^2]A$
  • absorbing 분포의 경우:$A=1e^T_m$으로 생각할 때 역시 $AA=A$를 만족한다. 그렇기에 역시 polynomial하게 표현할 수 있다. 이때에는 m번째 column에 빠지면 다시 나올 수 없으니 masking이 안된 분포를 기준으로 확률을 적용하면 된다.
    점점 t가 지날수록 I를 유지하는 확률 $\tilde \alpha_t=\prod_{i=0}^t(1-\beta_i)$에서 $\bar Q=\tilde \alpha_tI+(1+\tilde\alpha_t)1e_m^T$
• matrix exponentials tailor 급수에서 $e^x=\sum_{n=0}^\infin \frac{x^n}{n!}$이기 때문에 임의의 transition rate matrix $R$을 가지고 만든 matrix exponential을 $Q_t=\exp(\alpha_tR)=\sum^\infin_{n=0}\frac{\alpha^n}{n!}R^n$로 설정하면 곱셈이 합이 되기 때문에 ... 우선 pass
  

3.1 Choice of Markov transition matrices for the forward process

D3PM의 장점중 하나는 데이터 corruption과 denoising을 $Q_t$로 조절할 수 있음. 이는 gausian noise만 더하는 continuous diffusion과 다르다.

• 여기에서 $Q_t$의 제한은 row의 합이 1인 것과 $\bar Q_t$가 known stationary distribution으로 가는 것이다.
• 이는 쉽게 달성이 가능하다 Doubly-Stochasic matrix(row, column의 합이 1인 matrix)면 무조건 uniform distribution으로 가는 것을 만족한다. 만약 $\pi_i=1/K$일때 $Q\pi=\pi$ 즉 eigenvalue가 1인 eigenvector가 된다.
  이에 따라서 Perron-Frobenius theorem에 의해서 uniform distribution으로 수렴 (우선 pass)
  

이에 따라서 $Q_t$에 domain knowledge를 넣을 수 있다.

중요한 부분이기에 하나씩 정리

• uniform distribution: $Q_t=(1-\beta_t)I+\beta_t/K11^\top$으로 대각선은 $(1-\frac{(K-1)\beta_t}{K})$이고 나머지는 $\frac{\beta_T}{K}$인 matrix. doubly stochastic하기 때문에 uniform 분포로 수렴한다.
• Absorbing state: 예를 들어서 $\begin{bmatrix}1-\beta_t &0 &\beta_t\\0&1-\beta_t &\beta_t\\0&0&1\end{bmatrix}$과 같이 한번 특정 상태로 빠지면 다시 나올 수 없고 수렴하는 구조. text에서 [MASK] token으로 masking을 하는 경우 등에 사용
  당연히 전부 수렴하는 것이 stationary distribution
  이미지의 경우에는 회색으로 수렴하게 만들 수 있다.
• Discretized Gaussian:
  아래와 같이 구성이되는데 의미는 normal gaussian 분포와 비슷한데 row wise로 index의 차이 i-j의 제곱에 비례하고 분모는 K-1 즉 class의 size에 달라진다.
  즉 $\mathcal N(j;i,\frac{(K-1)^2\beta_t}{8})$을 의미한다.
  밑에 분자는 가능한 전체 거리로 나누어주는데 이게 분자를 다 합쳐도 나눠주는 양이 매우 많아서 row 전체를 다 합쳐도 1이 안되기에 대각선은 1에서 나머지 확률의 합을 빼준다.
  doubly stochastic하기에 uniform으로 수렴

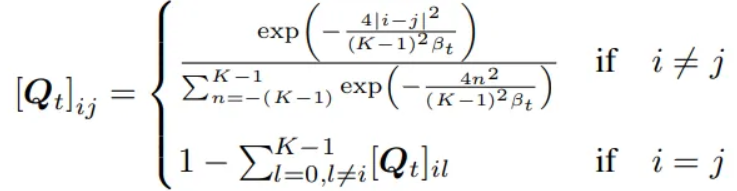
• Text embedding distance: text embedding은 유사도에 따라서 거리가 존재한다.
  거리로 K-nearest neighbor로 거리를 측정해서 $[G]_{ij}=1$ if i is K-nearest neighbot of j 로 구성
  이후 symmetric하게 만들기 위해서 $A=(G+G^\top)/(2k)$로 구성 2k로 나눠주는 이유는 각 column의 합이 k였는데 이를 transpose로 더해준 것으로 총 2k가 더해지기에 2k로 나눠준다.
  이후 $[R]_{ij} =\begin{cases} -\sum_{l \neq i} A_{il} & \text{if } i = j, \\A_{ij} & \text{otherwise}.\end{cases}$로 transpose rate matrix를 구성 이 덕분에 doubly stochastic하게 구성이 된다. (symmetric한 상태에서)
  그럼 대각선은 -가 나오고 각 행과 열의 합이 0이 나오는데
  이후 $Q_t=\exp(\alpha_tR)=\sum^\infin_{n=0}\frac{\alpha_t^n}{n!}R^n$을 하면 R의 row 합이 0이라서 $Q_t$의 row sum이 1이 되고 doubly stochastic하기에 uniform distribution으로 간다고 한다.
  corruption이 의미있는 단어 위주로 바뀌기 때문에 복원하기 더 쉬워진다고 한다.

3.2 Noise schedules

앞에서 Noise에 넣은 $\beta_t$를 어떻게 스케줄링할지

• linear: discrete gaussian의 경우 linear하게 조절.
• cosine: uniform의 경우 cosine으로 scheduling
  Improved Denoising Diffusion Probabilistic Models논문에서 noise를 cosine으로 scheduling을 하였을 때 마지막에 느리게 noise로 되는 과정에서 이점을 얻을 수 있었다고 함.
  $\bar\alpha_t=\frac{f(t)}{f(0)},f(t)=\cos(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2})^2,\beta_t=1-\frac{\bar \alpha_t}{\bar\alpha_{t-1}}$이다.
• general의 경우: $x_0$과 $x_t$의 mutual information을 $I(x_t;x_0)\approx(1-\frac{t}{T})H(x_0)$로 정하였을 때 obsorbe의 schedule이 $\beta_t=(T-t+1)^-1$이 되었다고 함.

3.3 Parameterization of the reverse process

reverse process $p_\theta(x_{t-1}|x_t)$를 parameterization을 하는 과정

$p_\theta(x_{t-1} \mid x_t) \propto \sum_{\tilde{x}_0} q(x_{t-1}, x_t \mid \tilde{x}_0) \tilde{p}_\theta(\tilde{x}_0 \mid x_t).$로 논문은 모델링을 하였는데 굳이 왜 이렇게 작성을 했는지 모르겠다. 구현이 된 내용도 다르다.

우리의 목적은 $\sum_{i>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))$를 학습하는 것이기에 이를 위주로 모델링이 되어야 한다.

실제로 사용되는 내용은 다음과 같다.

$q(x_{t-1}|x_t)=\frac{\sum_{x_0}q(x_{t-1},x_t,x_0)}{q(x_t)}=\frac{\sum_{x_0}q(x_{t-1}|x_t,x_0)q(x_0|x_t)q(x_t)}{q(x_t)}=\sum_{x_0}q(x_{t-1}|x_t,x_0)q(x_0|x_t)=\mathbb E_{q(x_0|x_t)}[q(x_{t-1}|x_t,x_0)]$이렇게 유도가 되고 여기서 $q(x_0|x_t):=\tilde p_\theta(x_0|x_t)$로 모델링 해서 $\tilde x_0$의 분포를 구해서 진행이 된다.

그럼 $\tilde p_\theta(x_0|x_t)$가 원본을 잘 모델링 하면 $p_\theta(x_{t-1}|x_t)=\sum_{x_0}q(x_{t-1}|x_t,x_0)\tilde p_\theta(x_0|x_t)$에서 $\tilde p_\theta(x_0|x_t)$가 $x_0$의 원본 class에 1을 줄 것이고 KL divergence는 0이 된다.

아래는 실제 구현.

#logit shape (batch, 3, 32, 32, class)
true_q_posterior_logits = self.q_posterior_logits(x, x_t, t)
pred_q_posterior_logits = self.q_posterior_logits(predicted_x0_logits, x_t, t)

dist1 = true_q_posterior_logits.flatten(0,-2)#(batch*3*32*32,class)
dist2 = pred_q_posterior_logits.flatten(0,-2)#(batch*3*32*32,class)

out = torch.softmax(dist1 + self.eps, dim=-1) * (
    torch.log_softmax(dist1 + self.eps, dim=-1)
    - torch.log_softmax(dist2 + self.eps, dim=-1)
    )#qlog(q/p)

그런데 바로 logit을 예측해서 진행하지 않고 굳이 0을 예측하고 다시 $x_t$를 예측해서 돌아오는 식으로 구성하는 이유는?
이전에

$q(x_{t-1}|x_t,x_0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}=\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)}$에서 $q(x_t|x_{t-1})$이 0인 state는 고려되지 않음. 결국 $Q_t$의 sparse한 것이 reverse에도 영향을 미치는 것인데 만약 전체를 예측해야하면 이 $Q_t$의 sparse함이 고려되지 않는다. 그러나 $p_\theta(x_0|x_t)$를 예측하고 다시 복구하는 식으로 진행이 되면 $Q_t$의 sparse함은 자동으로 적용이 되기에 이를 inductive bias로 사용할 수 있다.

결국 $\tilde p_\theta(x_0|x_t)$를 학습하기 때문에 k-step 예측도 가능

• logistic으로 $\tilde p_\theta(x_0|x_t)$에 순서 inductive bias 넣기 각각을 바로 예측하는 것이 아니라 loc, scale 즉, mean, var을 예측하고
  이를 토대로 bin을 잘라서 확률 분포를 예측하는 것
  왜 이게 inductive bias를 주냐 단순히 1개의 pixel의 값을 classification하는 것이 아니라 근처에 있는 것도 비슷한 값을 가진다는 것을 모델이 알 수 있게됨
  

3.4 Loss function

간단하게 원래 elbo loss에 cross entropy loss term을 추가

$L_\lambda=L_{elbo}+\lambda\mathbb E_{q(x_0)}\mathbb E_{q(x_t|x_0)}[-\log \tilde p_\theta(x_0|x_t)]$

4 Connection to existing probabilistic models for text

• BERT is a one-step diffusion model: absorbing + uniform matrix로 구성하면 BERT와 동일하게 구성이 된다. 점점 데이터가 [MASK]로 바뀌고 이를 복구하기 때문.
• Autoregressive models are (discrete) diffusion models: forward시에 점점 뒤에서부터 각 t마다 데이터를 [MASK]처리하면 reverse에서 앞에서부터 복구하게 된다.
  $N=T:q([x_t]_i|x_0)=[x_t]_i\quad \text{if} \quad i<N-t \quad\text{else}\quad [MASK]$
  이렇게 deterministic하게 진행.
  $q([x_{t-1}]_i|x_t,x_0)=\delta_{[x_t]_i}$if i$\ne T-t$ else $\delta_{[x_0]_i}$
  그렇기에 $q(x_{t-1}|x_t,x_0)$은 delta distribution
  이때 재밌는건 복구할 때 $D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))$의 $q(x_{t-1}|x_t,x_0)$부분이 delta distribution이라서 $D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))=-\log p_\theta([x_0]_i|x_t)$로 cross entropy로 구성이 된다.
• Masked Language-Models (MLMs) are diffusion models:
  그냥 앞에서 absorbing으로 전부 [MASK]로 복구하는 것이 사실상 동일.

5 Text generation

dataset

• text8: 영어 wikipedia에서 가져온 것
• LM1B: 영어 sentence dataset

모델 3가지

• uniform: uniform corruption, cosine scheduling
• absorbing: absorbing corruption, mutual information schedule
• NN: nearest neighbot, mutual information schedule

text8

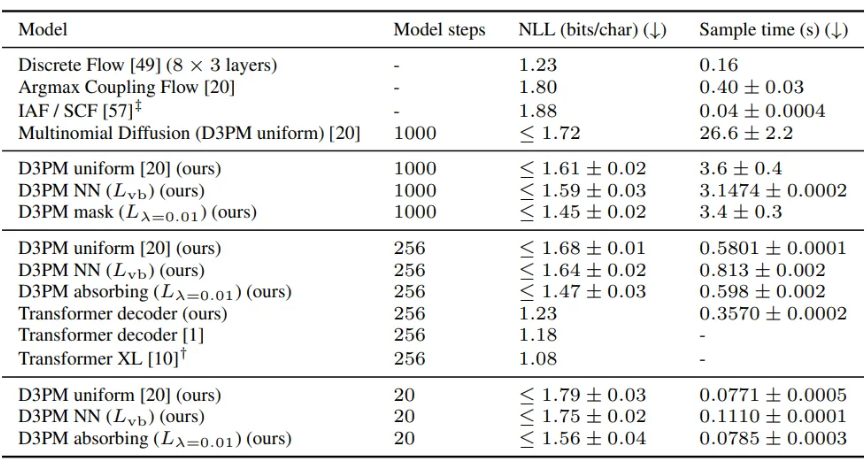
absorbing이 제일 성능이 좋았다.

non autoregressibe model을 이기는데 Discrete Flow 빼고는 다 이겼다.

step을 20으로 줄여도 성능이 잘 나옴. 이러면 decoder의 속도를 5배 정도 빠르게 이긴ㄷ.

nearest neighbor는 uniform과 큰 성능 차이 없었음.

5.2 Text generation on LM1B

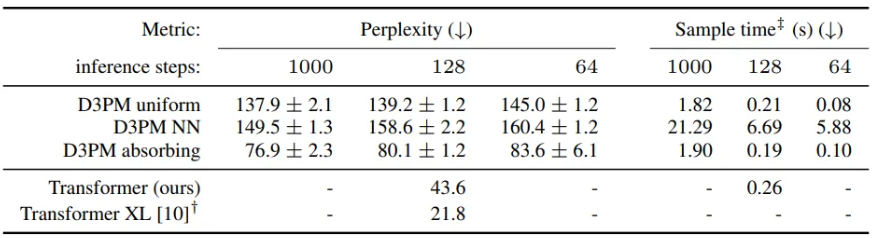
역시 absorbing이 제일 성능이 좋았다.

sentence는 나누는 것은 sentence piece vocab size 8192로 진행

nearest neighbot는 uniform보다 더 성능이 안좋음. 안쓰는게 나을 것 같다.

6 Image generation

cifar 10으로 진행

• uniform: cosine scheduling
• gaussian: $\beta_t=(T-t+1)^{-1}$
• absorbing: ddpm linear schedule

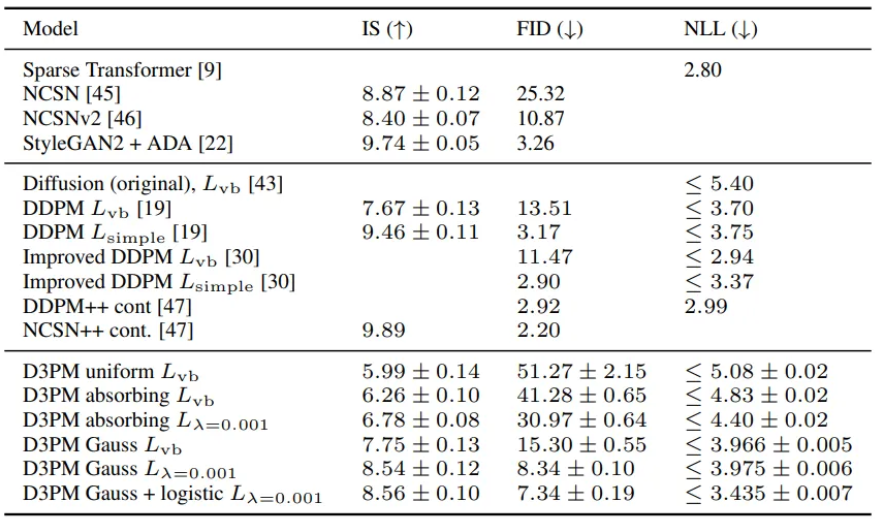
inception score → pretrain된 inception v3 모델의 kl divergence score

Frechet Inception Distance → pretrain된 inception v3 모델로 측정. 마지막 pooling layer의 activation으로 거리를 측정해서 진행

NLL → negative log lilekihood elbo로 측정

lotistic까지 사용한 모델의 NLL은 상당히 좋아서 기존의 DDPM을 이긴다.

나머지 IS, FID는 outperform하지는 못하지만 준수한 성능을 보여줌