디퓨전 elbo 증명

세미나 자료 준비하면서 정리

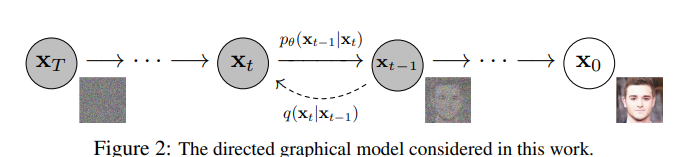
우선 간단한 정리
$p(x_0,x_1,...,x_T)=p(x_0|x_1)p(x_1|x_0)...p(x_{T-1}|x_T)p(x_T)\\=p(x_T)\prod_{i\ge1}p(x_{i-1}|x_i)$

$p(x_1,x_2,...,x_T|x_0)=p(x_1|x_0)p(x_2|x_1)...p(x_T|x_{T-1})\\=\prod_{i\ge1}p(x_{t}|x_{t-1})$
라고 하자
-log likelihood를 간접적으로 상승시키는 것이 목적

$-\log p_\theta(x_0)=-\log\int_{x_{1:T}}p_\theta(x_0,x_1,...,x_T)dx_{1:T}$

$=-\log\int_{x_{1:T}}p_\theta(x_{0:T})\frac{q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}dx_{1:T}$

$=-\log\mathbb{E}_{q(x_{1:T}|x_0)}[\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}]$
from Jensen's Inequality
$-\log p_\theta(x_0)\le\mathbb E_{q(x_{1:T}|x_0)}[-\log\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}]$

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log\frac{p_\theta(x_T)\prod_{i\ge1}p_\theta(x_{i-1}|x_i)}{\prod_{i\ge1}q(x_{t}|x_{t-1})}]$

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log p_\theta(x_T)-\sum_{i\ge1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1})}]$

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log p_\theta(x_T)-\sum_{i>1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1})}-\log\frac{p_\theta(x_0|x_1)}{q(x_1|x_0)}]$

이때 $q(x_t|x_{t-1})=q(x_t|x_{t-1},x_0)=\frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}$

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log p_\theta(x_T)-\sum_{i>1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}-\log\frac{p_\theta(x_0|x_1)}{q(x_1|x_0)}]$

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log \frac{p_\theta(x_T)}{q(x_T|x_0)}-\sum_{i>1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}-\log p_\theta(x_0|x_1)]$

$p_\theta(x_T):=p(x_T)$학습 x

$=\mathbb E_{q(x_{1:T}|x_0)}[-\log \frac{p(x_T)}{q(x_T|x_0)}-\sum_{i>1}\log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}-\log p_\theta(x_0|x_1)]$

결국
$-\log p_\theta(x_0)\le \mathbb E_{q(x_{1:T}|x_0)}[D_{KL}(q(x_T|x_0)||p(x_T))+\sum_{i>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))-\log p_\theta(x_0|x_1)]$

오른쪽 elbo를 줄이면 $-\log p_\theta(x_0)$가 줄어들어서 likelihood가 증가