[BOJ] 1720번 타일 코드 (Java)

백준 1720 타일 코드

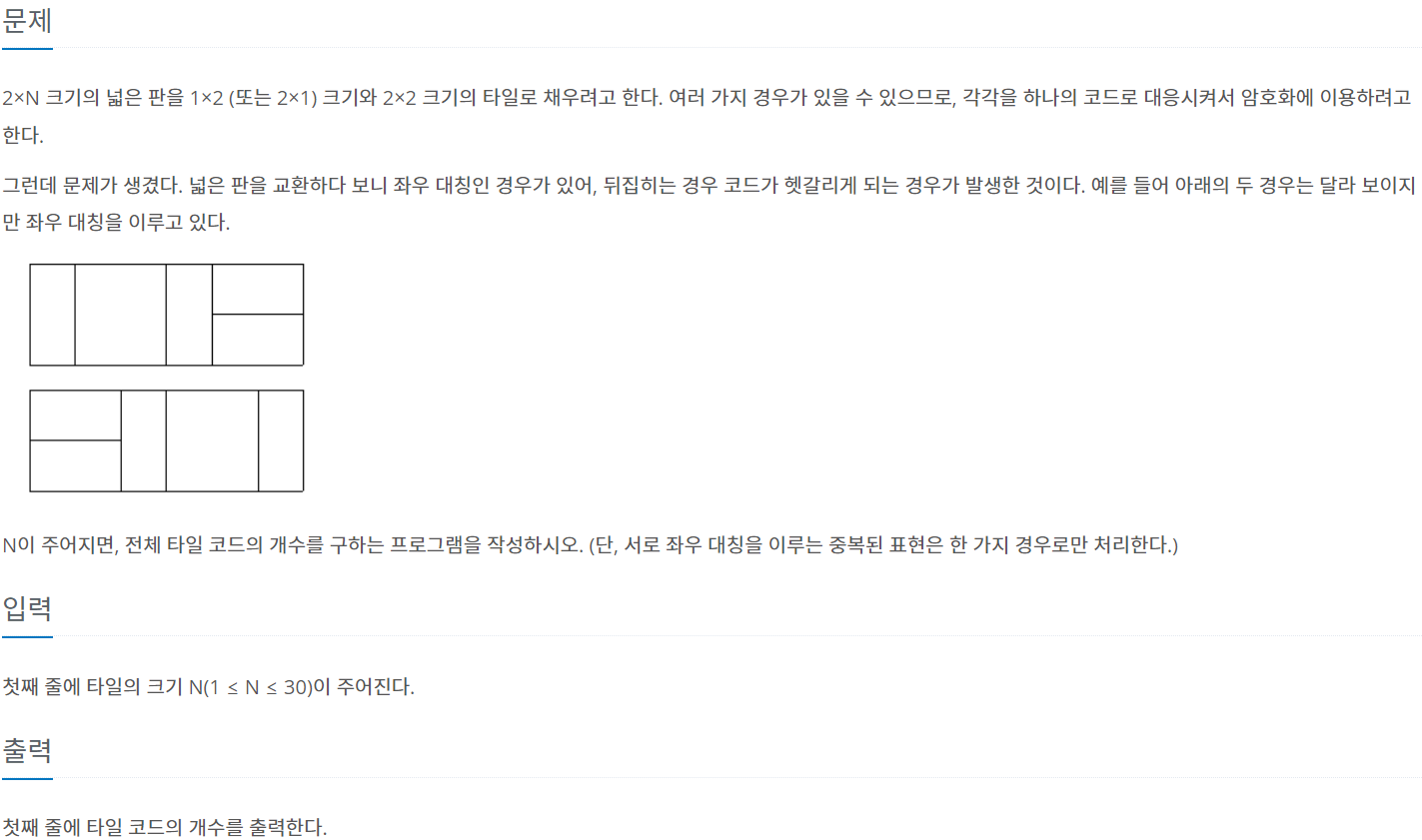
타일 문제는 DP 문제의 대명사이지만 대칭이라면 같은 타일로 취급해야 하는 문제다. 한 가지 아이디어가 포인트였다. 짝수인 경우와 홀수인 경우를 나누어 풀면 어렵지 않은 문제였다. 기본 DP를 바탕으로 모든 경우를 더한 후에 좌우대칭인 경우를 한 번 더 더하고 2로 나눈다.

좌우대칭이 되는 경우를 한 번 더 더하고 2로 나눈다.

import java.util.*;
import java.io.*;

public class Main {

    public static void main(String[] args) {
        try {
            int n, res = 0;
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
            n = Integer.parseInt(br.readLine());
            int [] dp = new int [n + 1];
            dp[0] = 1;
            dp[1] = 1;
            // 예외 처리
            if(n < 2){
                System.out.println(dp[n]);
                System.exit(0);
            }
            for(int i = 2; i <= n; i++){
                dp[i] = dp[i - 1] + dp[i - 2] * 2;
            }
            if(n % 2 == 1){
                // 홀수는 가운데가 1짜리 블록 고정하기 때문에 2로 나누기만 하면 된다.
                res = (dp[n] + dp[n / 2]) / 2;
            } else {
                // 짝수는 두가지 경우로 나눠야 한다 가운데가 세로로된 블록과 그 외의 블록
                res = (dp[n / 2 - 1] * 2 + dp[n / 2] + dp[n]) / 2;
            }
            System.out.println(res);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
}```