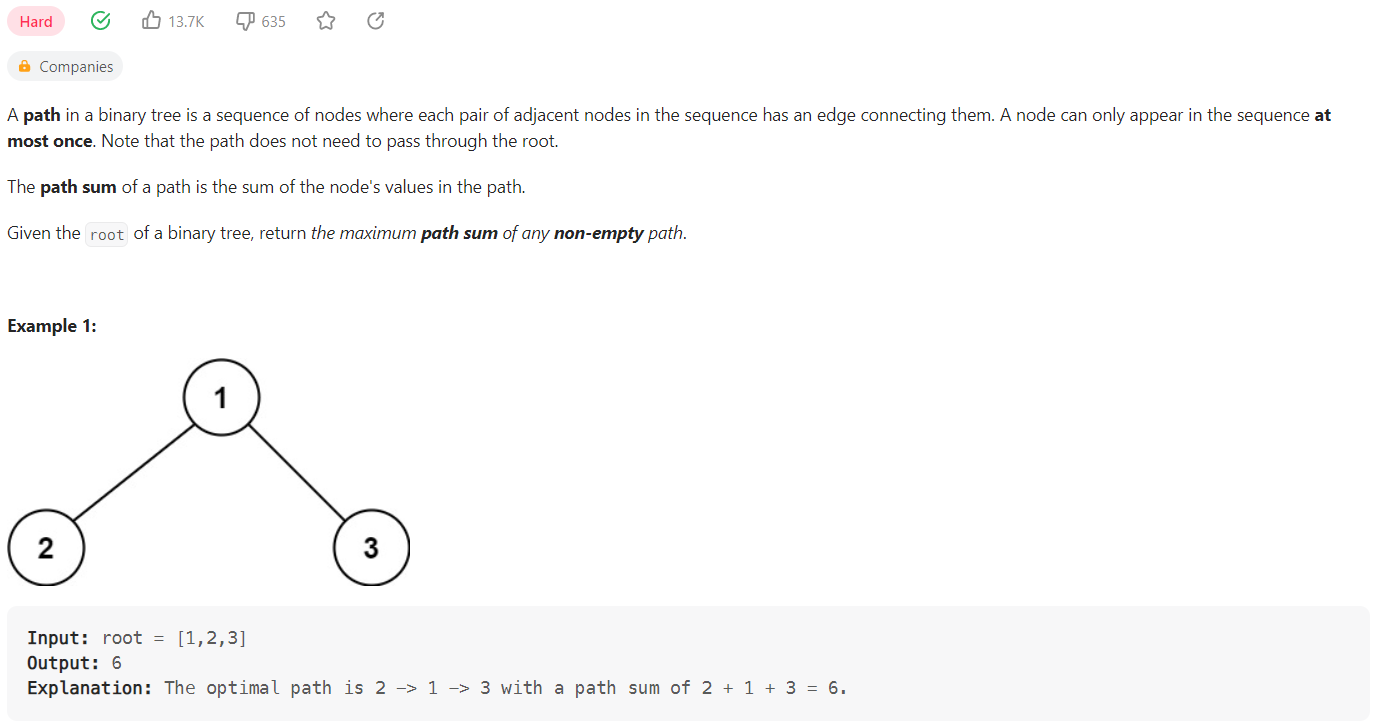
문제를 잘못 이해해 조금 돌아갔던 문제다. Top-down 접근법을 통해서 DFS 탐색을 통해 문제를 해결했다. 문제를 해결하는 포인트는 다음과 같았다.
- 부모 노드와 양옆에 자식 노드가 있는 경우에 왼쪽 자식 노드, 오른쪽 자식 노드 그리고 부모 노드를 동시에 연결하는 것은 불가능하다.
- 최댓값을 구하기 위해서 자식 노드의 path 값이 음수인 경우에는 자식을 버린다.
- 언제 최댓값이 나올지 모르기 때문에 모든 노드에서 최댓값을 업데이트한다.
- 모든 노드의 값이 음수인 경우는 그 어떤 노드를 선택하지 않는다. 이러한 예외를 처리하기 위해서 노드의 최댓값을 저장한다.
- 함수의 반환값은 부모와 해당 노드가 연결된다는 가정 하의 최댓값을 반환하지만, maxV 값은 지금까지의 path 최댓값을 저장한다.
official solution은 이와 같다.
class Solution: def maxPathSum(self, root: Optional[TreeNode]) -> int: max_sum = root.val def dfs(node): if not node: return 0 left_max = max(dfs(node.left), 0) right_max = max(dfs(node.right), 0) nonlocal max_sum max_sum = max(node.val + left_max + right_max, max_sum) return node.val + max(left_max, right_max) dfs(root) return max_sum
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.maxV = -1e9 # path 최댓값
self.maxN = -1e9 # 예외 처리를 위한 노드의 최댓값
def dfs(self, p) -> int:
if p.val <= 0:
self.maxN = max(self.maxN, p.val)
if p.left == None:
if p.right != None:
# 0을 선택했다는 것은 해당 path를 포기한다는 것
m = max(self.dfs(p.right) + p.val, 0)
self.maxV = max(self.maxV, m)
return m
else:
m = max(p.val, 0)
self.maxV = max(self.maxV, m)
return m
else:
if p.right == None:
m = max(self.dfs(p.left) + p.val, 0)
self.maxV = max(self.maxV, m)
return m
else:
l = max(self.dfs(p.left), 0)
r = max(self.dfs(p.right), 0)
m = max(l + p.val, r + p.val, 0)
self.maxV = max(self.maxV, m, l + r + p.val)
return m
def maxPathSum(self, root: Optional[TreeNode]) -> int:
self.dfs(root)
# 모든 노드가 음수일 경우를 고려한 예외처리(노드의 최댓값 반환)
return self.maxN if self.maxV == 0 else self.maxV
