Segment Tree(구간 트리)에 관하여

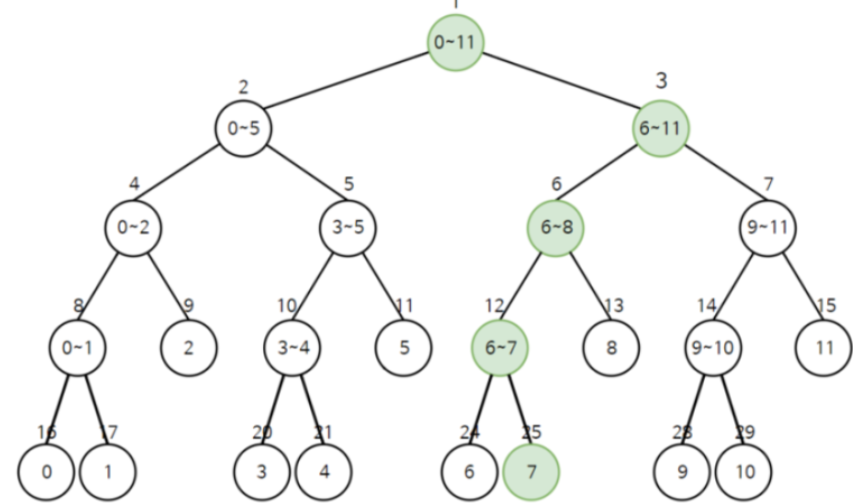
Segment Tree란?

자식 노드의 합을 저장하는 노드들로 이루어진 트리이다. 구간에서의 합을 구할 때 유리한 자료구조이다. 선형적으로 합을 구할 때는 시간 복잡도가 O(n)이 되는 반면에, 세그먼트 트리를 이용하면 구간 합을 구하거나 수정할 때 시간 복잡도가 O(logn)이 되어 상대적으로 빠르게 작동함을 알 수 있다. 세그먼트 트리에서 어떤 노드의 번호가 x일 때, 왼쪽 자식의 번호는 2 * x, 오른쪽 자식의 번호는 2 * x + 1이 된다. 단, 세그먼트 트리에서 루트 노드는 1로 시작한다.

• 리프 노드: 배열의 수 자체
• 다른 노드: 왼쪽 자식과 오른쪽 자식의 합을 저장

이 그림에서 2 ~ 4까지 합

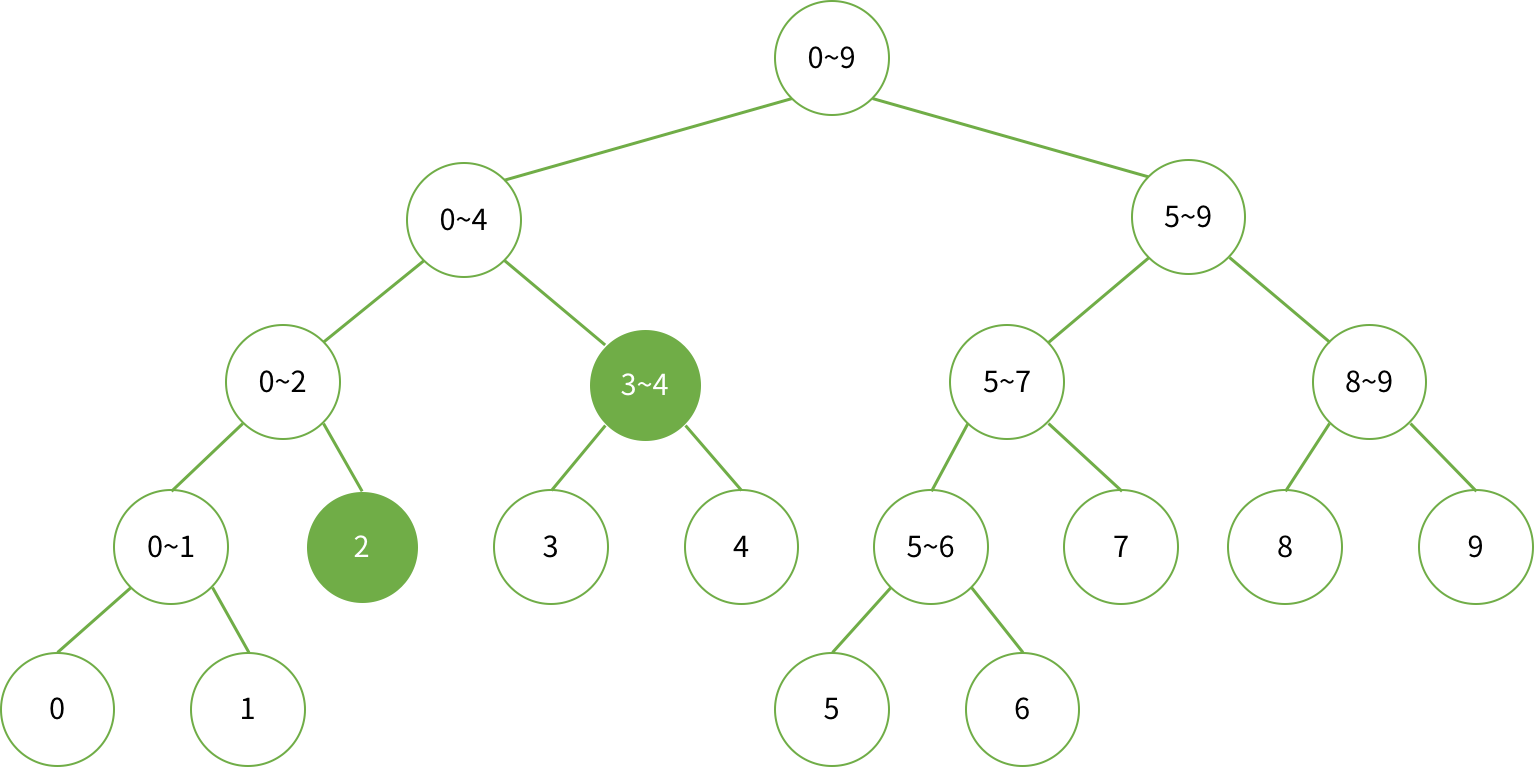
5 ~ 8까지 합

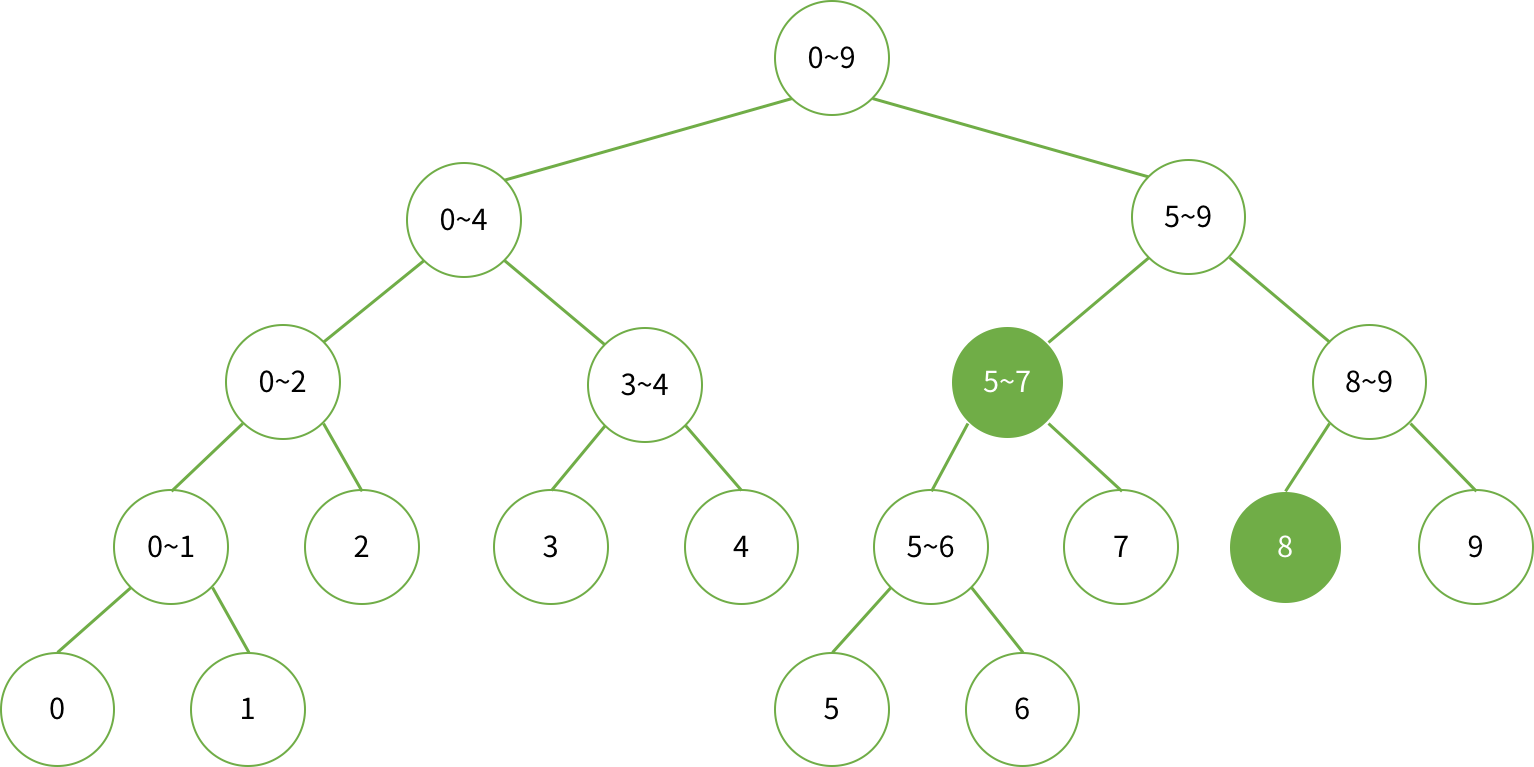
수정

중간에 값을 수정한다면, 그 숫자가 포함된 구간을 담당하는 노드를 모두 변경해 줘야 한다.

트리 생성 (Python)

inputList에 트리의 리프 노드 값들이 있다는 가정 하에 코드를 짰다.

def init(start, end, nodeNum):
    if start == end: 
        tree[nodeNum] = inputList[start]
        return tree[nodeNum]

    mid = (start + end) // 2

    tree[nodeNum] = init(start, mid, nodeNum*2) + init(mid+1,end,nodeNum*2+1)
    
    return tree[nodeNum]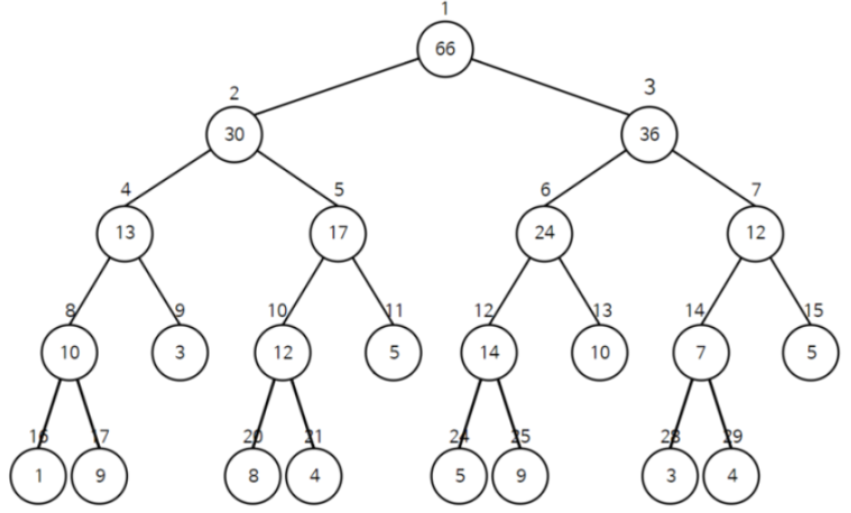

구간 합 구하기 (Python)

구간 합을 구할 때는 케이스를 잘 분리하는 것이 중요하다.

• start: 현재 탐색하는 노드의 구간 합 시작 범위
• end: 현재 탐색하는 노드의 구간 합 끝 범위
• nodeNum: tree에서의 node 번호
• left: 원하는 구간 합 시작 범위
• right: 원하는 구간 합 끝 범위

def tree_sum(start, end, nodeNum, left, right):
    if (left > end) or (right < start):
        return 0

    if (left <= start) and (end <= right):
        return tree[nodeNum]

    mid = (start + end) // 2

    return tree_sum(start, mid, nodeNum*2,left,right) + \
    tree_sum(mid+1,end, nodeNum*2+1,left, right)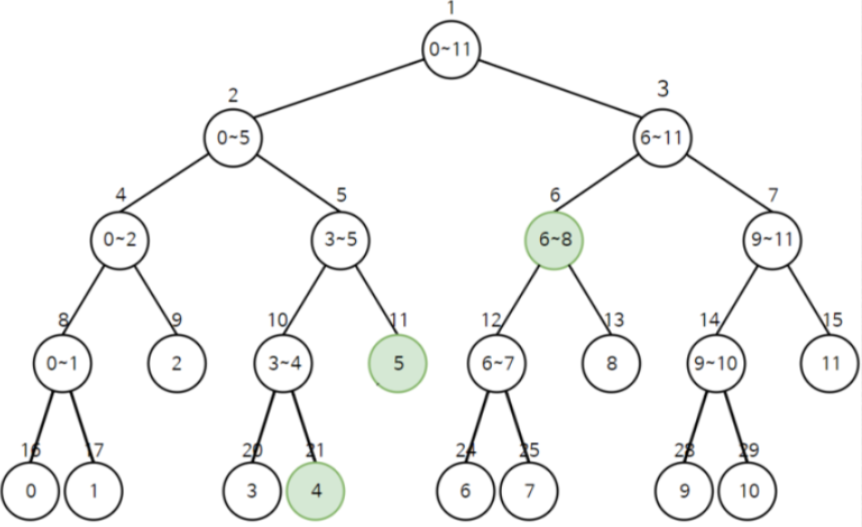

값 수정하기 (Python)

수정하는 노드를 포함한 모든 노드를 수정한다.

def change(start, end, nodeNum, idx, fixed):
    if idx < start or idx > end:
        return 
    
    tree[nodeNum] += fixed 
    if start == end:
        return

    mid = (start + end) // 2
    change(start, mid, nodeNum*2, idx, fixed)
    change(mid + 1, end, nodeNum*2+1 , idx, fixed)