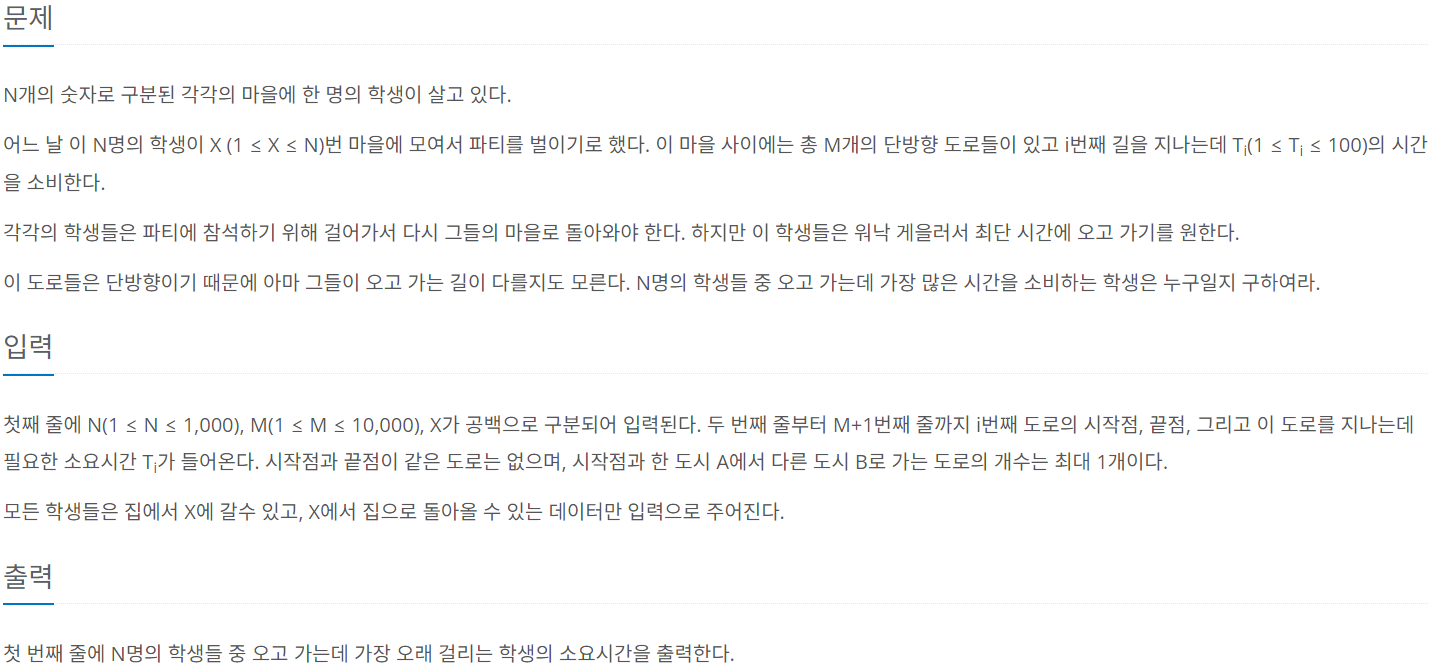
다익스트라를 활용해서 푸는 문제라는 것은 금방 알 수 있었지만, 이 문제를 어떻게 풀어야 할지 조금 고민했다. 주어진 길을 기준으로 올때와 갈 때를 나누어서 다익스트라 알고리즘을 활용해야 했고, 어떻게 해야 효율적으로 풀 수 있을지 고민했다.
1. 어디에서 오는지를 저장할 리스트 (각 도시에서 X까지의 최단거리를 찾기 위해)
2. 어디로 가는지 저장할 리스트 (X에서 되돌아 갈 때의 최단거리를 찾기 위해)
두 가지로 나누어 리스트를 저장하고 다익스트라를 두 번 돌리면 비교적 우아하게 풀 수 있는 문제였다.
import sys
from collections import deque
def solution():
inp = sys.stdin.readline
n, m, x = map(int, inp().split())
flist = [[] for _ in range(n + 1)]
tlist = [[] for _ in range(n + 1)]
fdp = [1e9] * (n + 1)
tdp = [1e9] * (n + 1)
fdp[x], tdp[x] = 0, 0
for _ in range(m):
f, t, c = map(int, inp().split())
flist[f].append((t, c))
tlist[t].append((f, c))
q = deque()
q.append((x, 0))
while q:
pos, cost = q.popleft()
for next, c in flist[pos]:
if fdp[next] > cost + c:
fdp[next] = cost + c
q.append((next, fdp[next]))
q.append((x, 0))
while q:
pos, cost = q.popleft()
for next, c in tlist[pos]:
if tdp[next] > cost + c:
tdp[next] = cost + c
q.append((next, tdp[next]))
maxV = 0
for i in range(1, n + 1):
maxV = max(maxV, fdp[i] + tdp[i])
return maxV
if __name__ == "__main__":
print(solution())
