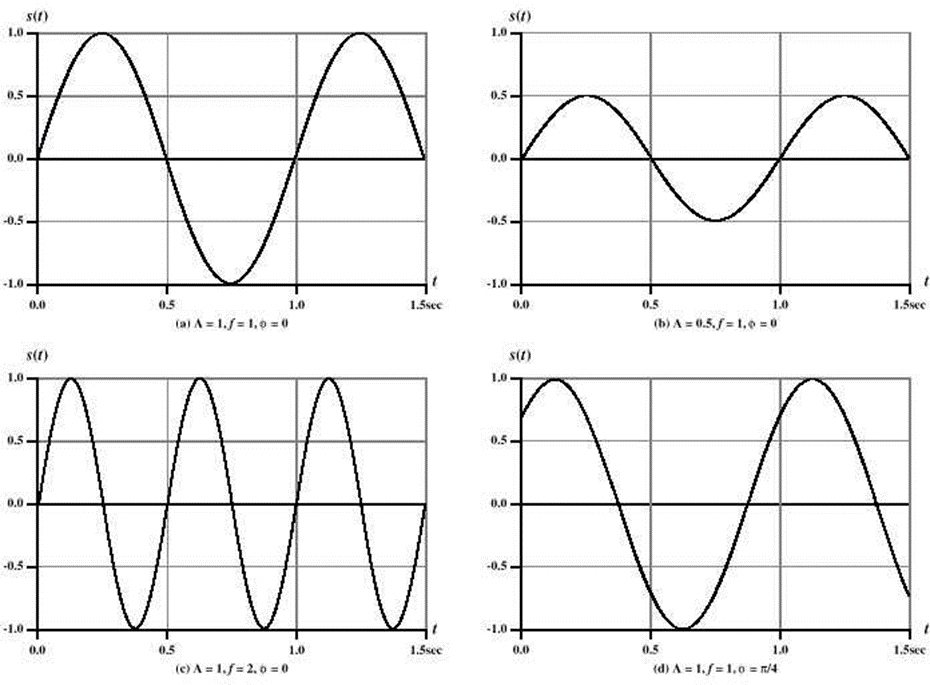
RF with Sine Graph
RF는 s(t) = A sin(2πft + Φ)의 Sine 그래프로 나타낼 수 있음
즉 t의 시간이 지났을때에 그 지점을 나타낼 수 있음
이때 A는 peak Amplitude(최대 진폭), f는 freqeuncy(주파수), Φ는 phase(위상)
ex )
Frequency vs Period
Frequency : 주파수 f. 단위시간당 몇번 반복하는지 횟수
Period : 주기 T. 한번 반복할 때 얼마나 걸리는지
이둘은 역수 관계. 즉, T = 1/f, f = 1/T
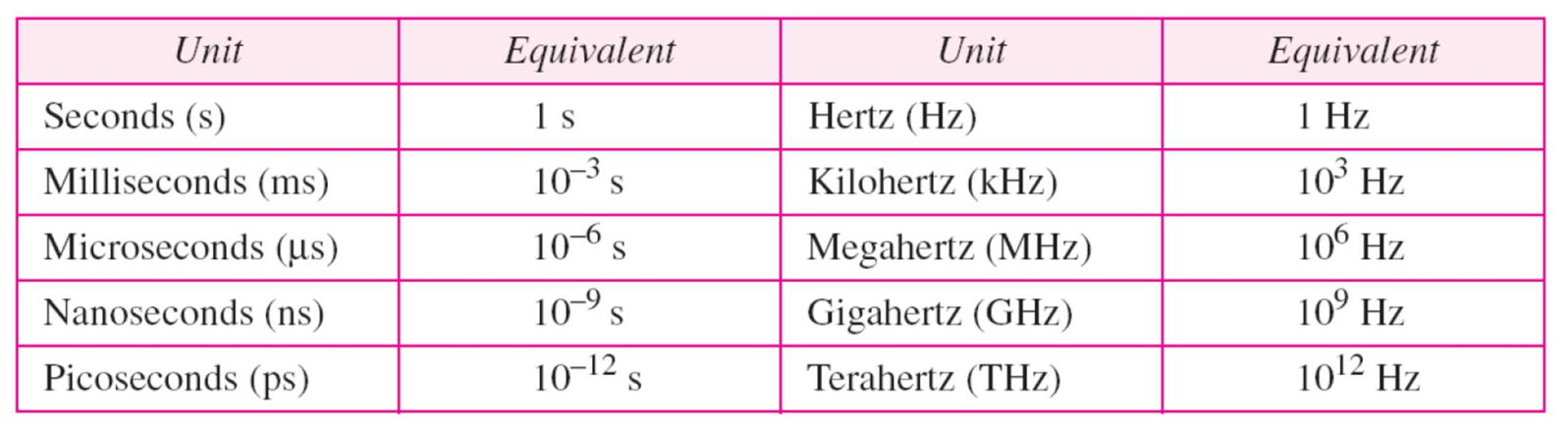
주파수의 단위는 Hz 주기의 단위는 s
이때 주기가 1s라면 1Hz. 주파수와 주기가 역수관계 이므로 주기가 1ms(10^-3 s)라면 주파수는 1kHz(10^3 Hz)임
Wavelength λ
파장의 길이를 알고싶을때 사용
λ = c/f 이때 c는 빛의 속도 310^8 m/s이다.
ex) f = 2GHz = 2 10^9 Hz => λ = (3 10^8)m/s / (2 10^9)s = 0.15m = 15cm
Signal
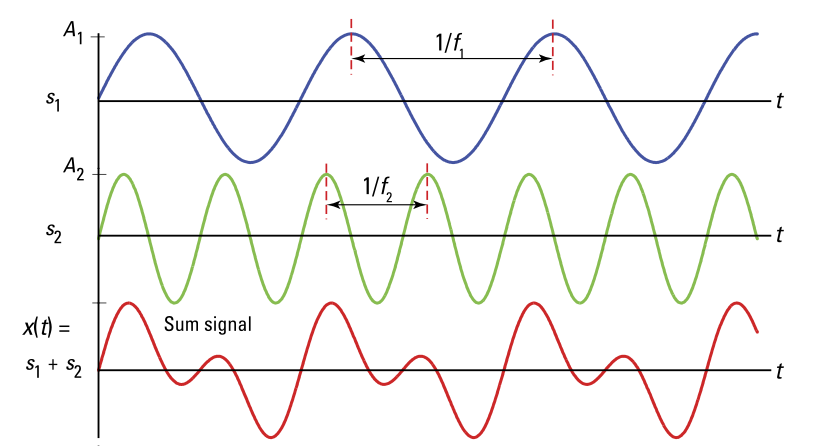
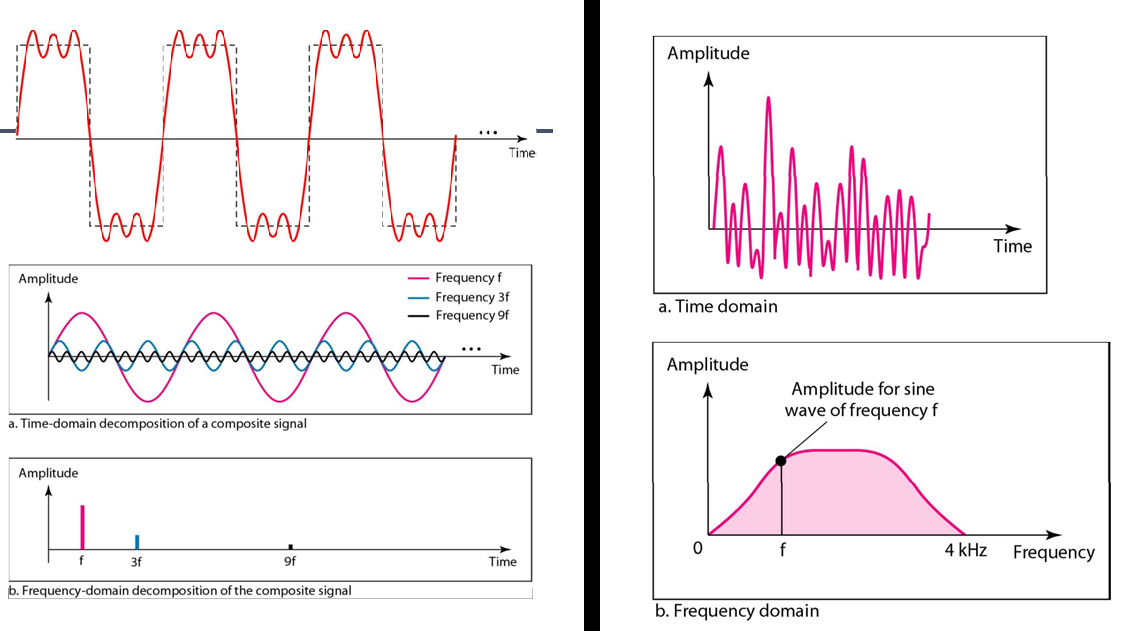
Signal = Sum of Sine Waves
이때 Signal은 가장 낮은 Freqeuncy를 가지고있는 Sine wave와 동일한 Frequency를 가짐
하나의 Sine wave만 가지고서는 신호 구분을 통한 해석이 어렵기때문에 여러개의 Sine wave의 조합으로 하나의 Signal을 만들어줌
위 그림에서 X축은 시간축, Y축은 Apmlitude. 이것은 Time domain임
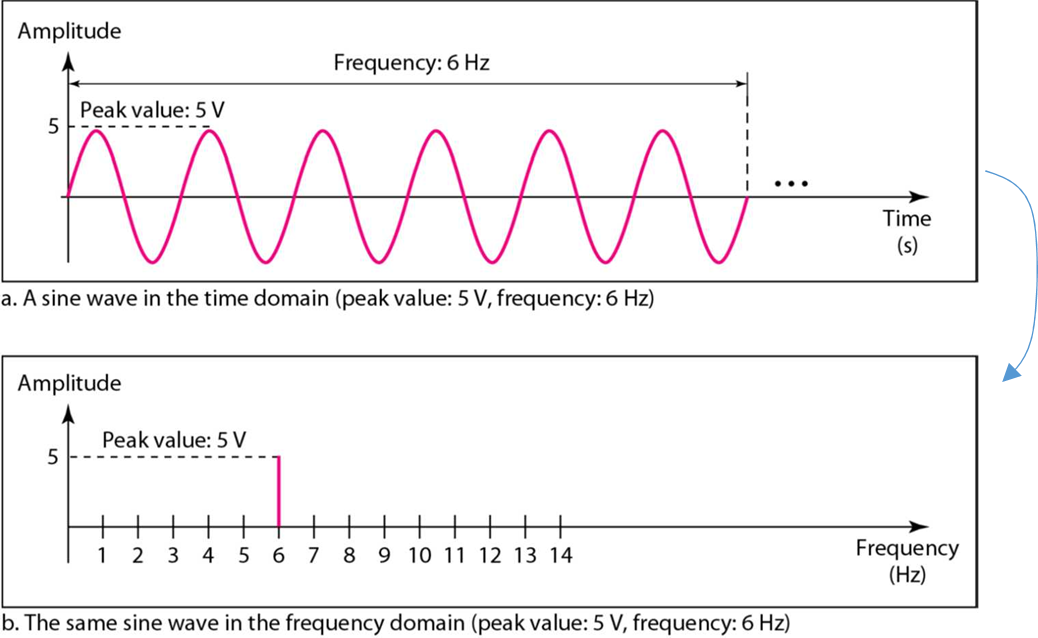
하지만 RF는 3개의 parameter가 존재하기때문에 Frequency domain으로도 나타낼 수 있음
위 그림은 최대 진폭이 5V이고, Frequency가 6Hz인 Sine wave를 나타낸 것이다.
위 그림은 Time domain이고, 아래 그림은 Frequency domain이다.
특정한 Sine wave가 들어간 Signal을 다룰때에는 Frequency domain이 더 유용하다.
=> 특정한 사이클을 가지고 반복되는 형태인 신호는 다른 세기를 같는 sine wave들을 합치면 만들 수 있다. 즉, 어떠한 주기성을 같는 신호라도 sine wave들의 합으로 만들 수 있다.
또, 그런 신호는 time-domain과 frequency-domain으로 다 나타낼 수 있다.
Fourier analysis
- If the composite signal is periodic, the decomposition gives a series of signals with discrete frequencies;
- if the composite signal is nonperiodic, the decomposition gives a combination of sine waves with continuous frequencies
즉 사진의 왼쪽 처럼 주기성을 가지는 Signal은 Frequency domain에서 이산된(분리된) 그래프로 나타 낼 수 있고, 오른쪽 처럼 비주기성을 가지는 Signal은 Frequency domain에서 연속된 그래프로 나타낼 수 있다.
Spectrum & Bandwidth
Spectrum : signal이 담고있는 frequency의 모든 range. 위에서는 1f, 3f, 5f
Fundamental Frequency : 제일 낮은 주파수. 위에서는 1f
Bandwidth : 최고 주파수와 최저주파수의 폭. 얼마나 두꺼운가. 한계가 있음. 무한대X
Absolute bandwidth : 스펙트럼의 폭, 최고 주파수 - 최저 주파수. 위에서는 4f
이때 어떤 주파수는 되게 강하지만, 어떤 주파수는 굉장히 작을수도 있기때문에
Effective bandwidth : 99% 이상의 에너지를 가지고있는 주파수의 폭. 만약 위에서 99%의 에너지가 1f와 3f에 몰려있다면 2f가 됨
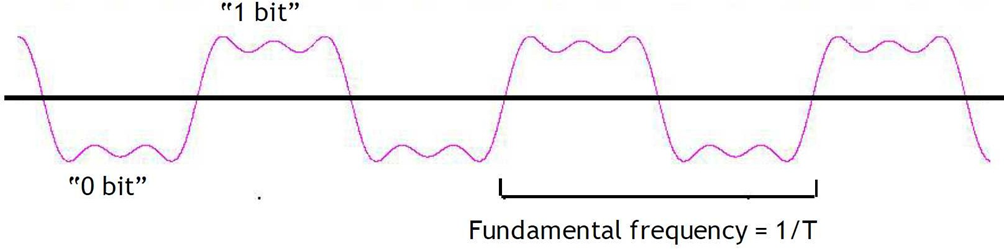
위 사진처럼 일정 수준 위의 값들은 1비트, 아래값들은 0비트라고 하자.
그리고 한 주기당 2개의 비트를 전송한다고 하자.
만약 주기가 1 μs(10^-6)이라고 한다면, f는 1/T이므로 1 MHz(10^6)가 된다.
이때 한 주기안에 두개의 비트가 있으므로 data rate은 2* 10^6 = 2Mbps가 된다.
위 예시를 통해 Frequency가 높다면, data rate이 늘어나게 된다는 점을 알 수 있다.
따라서 무조건 Frequency를 높게 하면 좋지만, 무선으로 보내기때문에 낮은 주파수대역은 멀리까지 가지 못한다. 따라서 적절한 Frequency를 사용하는것이 좋음
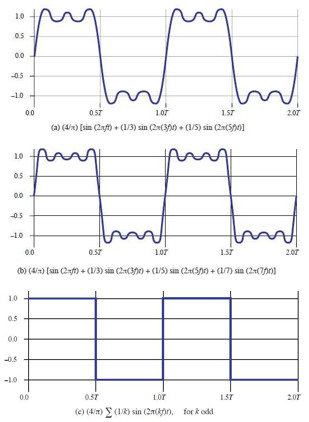
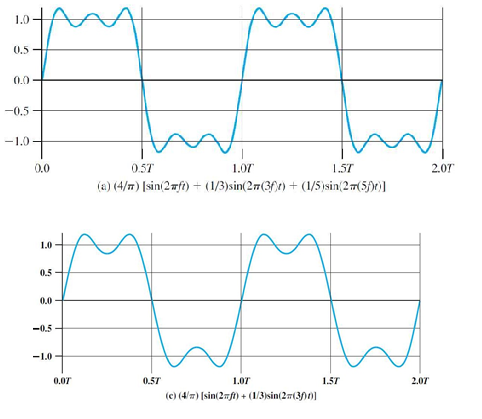
위 사진의 첫번째 그래프는 그 아래 수식으로 알수 있듯이 1f, 3f, 5f로 만든 Signal이고 bandwidth는 4f이다.
두번째 그래프는 1f, 3f, 5f, 7f로 만든 Signal이고 bandwidth는 6f이다.
마지막 그래프는 극한값으로 모든 소수f 즉, 1f, 3f, 5f,,,,nf로 만든 Signal이고 bandwidth는 무한으로 발산할 것이다.
세 그래프의 차이점을 통해 bandwidth가 증가할수록 Signal quality가 증가함을 알 수 있다.
하지만 앞서 말했듯, Bandwidth를 무한대로 사용하면 모든 신호에 간섭하게 되므로 Bandwidth의 한계가 있다.
a는 스펙트럼이 [f, 3f, 5f]이고 bandwidth가 4f인 Signal이다.
a - Ex1) 이때 bandwidth의 범위를 4MHz로 한다면 f가 1MHz가 되어야한다.(4MHz = 4f)
그리고 1MHz일때 총 2개의 비트가 전송이 되므로 data rate은 2Mbps가 된다.
a - Ex2) 이때 bandwidth의 범위를 8MHz로 한다면 f가 2MHz가 되어야한다.(8MHz = 4f)
그리고 2MHz일때 총 4개의 비트가 전송이 되므로 data rate은 4Mbps가 된다.
c는 스펙트럼이 [f, 3f]이고 bandwidth가 2f인 Signal이다.
c - Ex1) 이때 bandwidth의 범위를 4MHz로 한다면 f가 2MHz가 되어야한다.(4MHz = 2f)
그리고 2MHz일때 총 4개의 비트가 전송이 되므로 data rate은 4Mbps가 된다.
c - Ex2) 이때 bandwidth의 범위를 8MHz로 한다면 f가 4MHz가 되어야한다.(8MHz = 2f)
그리고 4MHz일때 총 8개의 비트가 전송이 되므로 data rate은 8Mbps가 된다.
결론
- Bandwidth의 범위가 증가하면, Data rate도 증가 (a-ex1과 ex2 / c-ex1과 ex2)
- Bandwidth의 범위가 같을때에는 signal quality가 증가하면 Data rate는 감소 (a-ex1와 c-ex1 / a-ex2와 c-ex2)
- Data rate이 같을때 Bandwidth 범위가 증가하면 Signal quality도 증가 (a-ex2과 c-ex1)
=> 모든 디지털 데이터는 0, 1로 나뉘어져있고, Signal quality가 엄청 좋아야하므로 무한 Bandwidth를 가져야한다.
하지만 Signal quality가 좋아지면 그에 따라 Data rate은 감소한다.
따라서 실용적인 이유로 인해 디지털 데이터는 아날로그 데이터로 변환해서 사용
Modulation & Demodulation 파트 참조
Reference
https://stackoverflow.com/questions/51926684/plotting-sum-of-two-sinusoids-in-python