
Multi-source BFS
BFS와 DFS에 대한 차이와 정의는 recursive DFS에 대해 설명했던 문제에 있다. [link] 동일 레벨의 노드들을 먼저 방문한 후 다음 레벨로 진행하는 것이다.
이 문제처럼 점점 "확산"해 나가는 문제에서는 코드가 간단한 DFS보다 BFS로 접근해야 하는데, 특히 multi-source(multi-root)로 접근하는 아이디어가 필요했다.
아래 그림처럼 숫자가 1씩 증가하면서 한칸씩 퍼져가는 경우를 생각해보자. BFS로 탐색을 했을 때 각 root에서 오직 한칸씩만 퍼지고 그 다음 레벨로 넘어가기 때문에 어떤 두 지점에서 출발한다고 하면 중간에서 만나게 된다. 자연스럽게 인접한 칸은 1 차이를 갖게 되는 것이다. 모든 칸을 채워야 하는 상황에서 지점A에서 가까운 지점은 오직 지점A에서의 탐색에서만 들르게 할 수 있다. 아래 문제를 보면 이해에 도움이 된다.
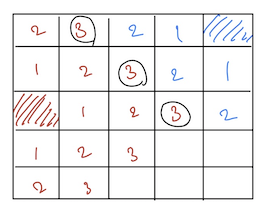
# multi-source BFS
queue = deque([root1, root2, root3])
while queue:
blah blahQuestion
0은 land, 1은 water로 이뤄진 matrix가 주어짐
새로운 matrix를 구성해라
- water는 0, land는 인접한 곳에서 0 또는 1씩 커져야 함
- 동서남북으로만 인접한다고 봄
example 1
[[1, 0],
[0, 0]]이 주어졌을 때
[[1, 0],
[2, 1]]이 땅의 모양

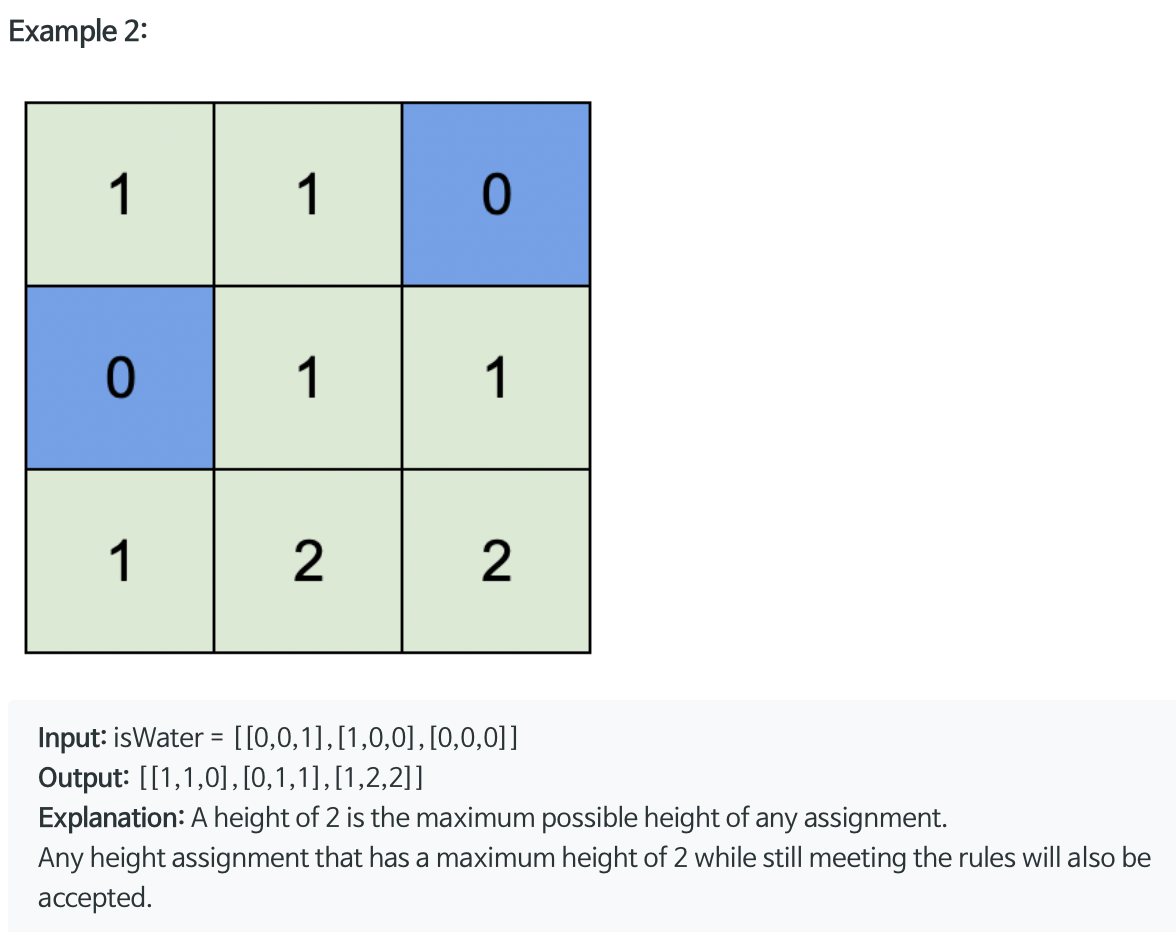
Solution
- 인접(다음 level)한 곳에서 +1씩 높아져야 하기 때문에 BFS로 동일 level부터 탐색하면서 숫자를 할당할 수 있도록 해야 한다.
Solution 1. 먼저 각각 water 지점들에서 출발하는 BFS를 돌린 후 각각 생성된 height_map들을 가지고 각 지점에서의 minimum value를 답으로 뽑아보았다.
Solution 2. water 지점들을 동일 level로 보고 queue에 넣은 후, BFS를 시작한다. 한 level씩 숫자 할당이 이뤄지는데, 결국 water 1과 water 2 지점의 중간에서 둘이 만나게 되고 차이가 1 이상 나지 않게 된다.
Sol1에 비해 탐색해야하는 지점이 현저히 줄어들어 통과할 수 time limit에 걸리지 않게 된다!!
PSEUDO sol1: 코드는 너무 길어서 맨 아래 github 페이지의 solution 1 참고
- answer_map (0으로 이뤄진 input matrix와 동일한 사이즈의 matrix)
- def BFS: BFS를 돌면서 answer map이 0이 아니면 기존 높이와 지금의 BFS에서의 높이 중 작은 쪽 할당, 0이면 높이 할당
- 모든 water 지점에서 BFS 시작
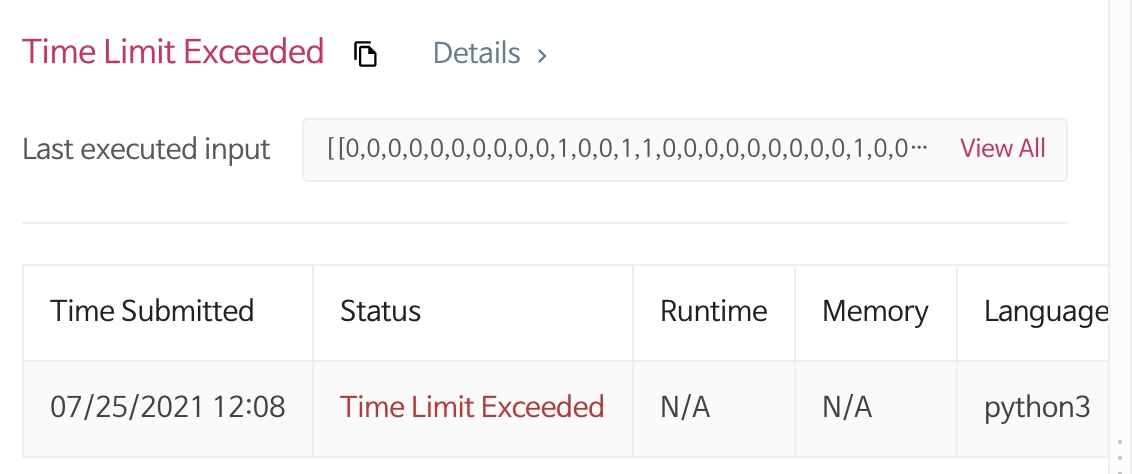
PSEUDO sol2
- water 지점들을 첫 queue에 담기
- 그대로 BFS 시작
answer_map에서 숫자가 할당되지 않은 부분만 탐색 & 숫자 할당
동일 레벨은 동일한 차순에서 탐색과 숫자 할당이 이뤄지기 때문에, 두 water 지점으로부터 동일한 지점에서 탐색이 만나게 된다. (잘 이해해볼 포인트!)
def sol_2(isWater):
r = len(isWater)
c = len(isWater[0])
newiswater = [[None for k in range(c)] for l in range(r)]
deq = deque()
for row in range(r):
for col in range(c):
if isWater[row][col] == 1:
deq.append([row, col])
newiswater[row][col] = 0
while deq:
row, col = deq.popleft()
for new_row, new_col in [(row+1, col), (row-1, col), (row, col-1), (row, col+1)]:
if 0 <= new_row < r and 0 <= new_col < c and newiswater[new_row][new_col] is None: # ()
newiswater[new_row][new_col] = newiswater[row][col] + 1
deq.append((new_row, new_col))
return newiswater

