
Sort의 종류는 참 다양하다...
Bubble, Quik, Insert, Merge 등... 세상에는 sort의 종류가 참 많다.
Radix sort는 무엇인가?
근데 먼저 Counting sort를 공부해야 했다...
5, 1, 3, 4, 1, 2, 5, 6 이라는 A 수열을 정렬한다고 하자
- 우선 최대 숫자 6을 참조하여 index 6까지 존재하는 '0'으로 이뤄진 B 배열을 만들어 보자
B = [0, 0, 0, 0, 0, 0, 0] - A 수열의 각 수가 몇 번 등장하는지를 B 배열에 카운트해보자
B = [0, 2, 1, 1, 1, 2, 1] - B 배열의 누적합으로 변경해준다.
B = [0, 2 (0+2), 3 (2+1), 4 (3+1), 5 (4+1), 7 (5+2), 8 (7+1)]
=> 1번 index (A 배열에서 숫자 1)의 2라는 누적합을 통해 A 배열의 숫자 1들이 정렬될 배열에 1, 2번째에 들어가야 한다는 걸 알게 되었다. - 결과로 나와야 할 N (A 배열의 총 수)개의 '0'으로 이뤄진 배열을 만든다.
output = [0, 0, 0, 0, 0, 0, 0, 0] - B 배열에서 가장 뒤에 있는 누적합을 통해 6의 위치를 조정해 보자. B 배열에 누적합이 8이라고 하면 6은 output의 8번째 자리 (7 index)에 위치해야 한다.
output = [0, 0, 0, 0, 0, 0, 0, 6]
그리고 다음에 또 6이 있는 경우도 있을 수 있으니 누적합 8을 7로 변경해 준다.
B = [0, 2, 3, 4, 5, 7, 7] - 위와 같이 수의 누적합을 이용하여 index 위치를 찾아주는 sort 방법이 Counting sort이다.
본격 Radix sort를 공부해보자
Radix Sort (기수 정렬)는 배열 요소의 각 자리수를 확인하여 미리 준비한 일명 자리수 배열에 위치하도록 하는 것이다. 해당 sort는 다른 수들과 비교를 통해 정렬을 하지 않는다.
1, 11, 20, 21, 35, 101, 50 를 정렬한다고 해보자
1) 1의 자리수로 0~9 인덱스에 위치하도록 먼저 정렬한다.
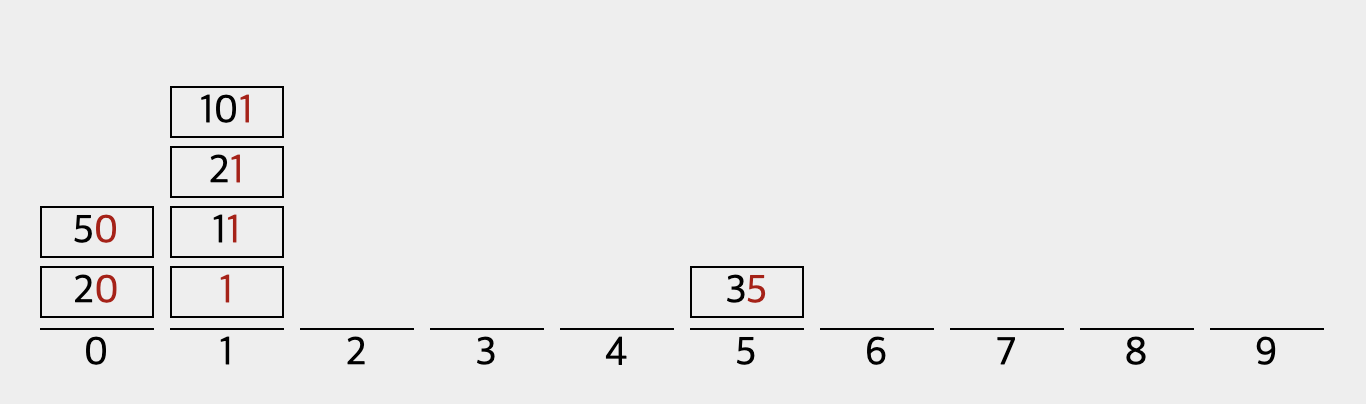
[20, 50, 1, 11, 21, 101, 35]로 정렬되었다.
2) 10의 자리수로 다시 0~9 인덱스에 위치하도록 정렬한다. (10이하의 수의 10의 자리수는 0으로 한다)
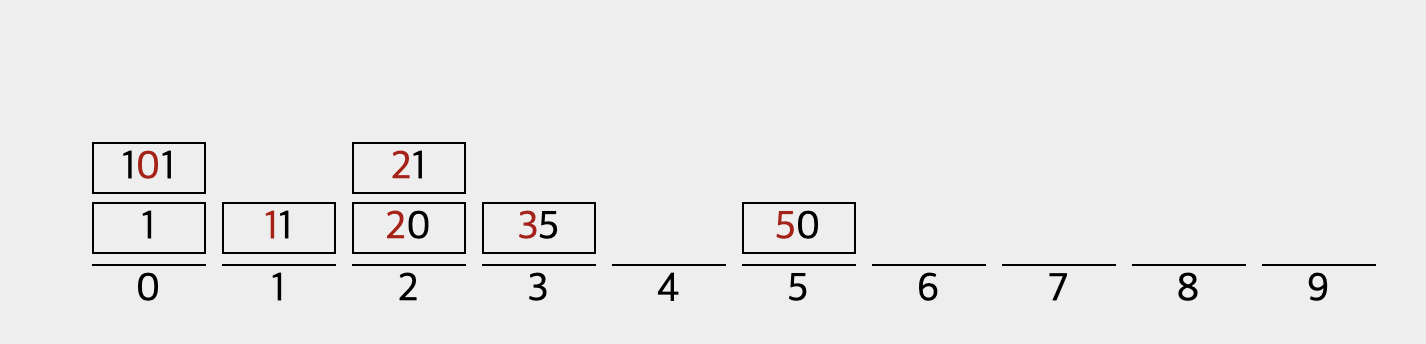
[1, 101, 11, 20, 21, 35, 50]로 정렬되었다.
3) 마지막 100의 자리수로 다시 0~9 인덱스에 위치하도록 정렬한다.
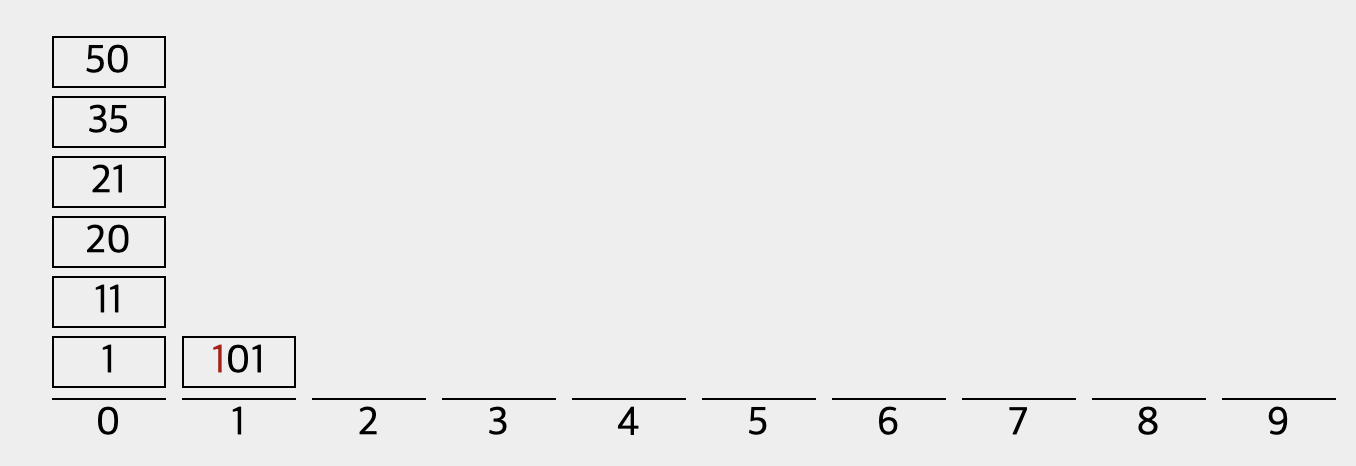
4) [1, 11, 20, 21, 21, 35, 50, 101]로 모든 정렬을 마친다.
Radix sort를 구현하려고 보니, Counting sort와 닮아 있는 부분이 많았다. 미리 0~9의 배열을 만들어 놓고 각 정렬하고자 하는 수를 그 배열의 인덱스로 매칭하여 정리하는 것이 공통점이었다.
구현
// 배열에서 가장 큰 수를 먼저 구한다. Radix의 범위를 정하기 위함이다.
function getMax(arr) {
return arr.reduce((max, item) => {
if (item > max) return item;
return max;
}, 0);
}
// 먼저 counting sort의 식을 구해보자
function countingSort(arr, radix) {
const N = arr.length;
// 재정렬하기 위한 준비 배열
const output = Array(N).fill(0);
// 0부터 9까지의 준비 배열 (각 자리수의 수의 누적합 계산을 위한 배열)
const count = Array(10).fill(0);
// 현재 자리수(radix: 1, 10, 100...)를 기준으로 배열의 0~9의 개수를 센다. 나중에 Radix sort에서 radix별로 계속 loop해 줄 예정이다.
arr.forEach((item) => {
const idx = Math.floor(item / radix) % 10;
count[idx]++;
});
// count[i]가 i까지의 누적 개수가 되도록 만든다.
count.reduce((totalNum, num, idx) => {
count[idx] = totalNum + num;
return totalNum + num;
});
// 아래 속성이 유지되도록 하기 위해 배열을 거꾸로 순회한다.
// 1. 가장 큰 값을 먼저 본다.
// 2. 가장 큰 값을 가장 마지막에 놓는다.
let i = N - 1;
while (i >= 0) {
const idx = Math.floor(arr[i] / radix) % 10;
// count[idx]: 현재 radix의 idx까지 누적 개수
// count[idx]개만큼 있으므로, 인덱스는 count[idx] - 1
output[count[idx] - 1] = arr[i];
count[idx] -= 1;
i--;
}
return output;
}
function radixSort(arr) {
// 음수의 정렬
let left = [];
//양수의 정렬
let right = [];
arr.forEach((item) => {
if (item >= 0) right.push(item);
else left.push(item * -1);
});
// 최대 수를 구하고...
let max = getMax(left);
// 1의 자리부터 시작...
let radix = 1;
// 최대 수의 자리수까지만 while...
while (parseInt(max / radix) > 0) {
// 정렬의 결과를 다시 left 배열로 할당한 후 radix 자리수를 10씩 곱해준다.
left = countingSort(left, radix);
radix *= 10;
}
max = getMax(right);
radix = 1;
while (parseInt(max / radix) > 0) {
right = countingSort(right, radix);
radix *= 10;
}
return left
// 양수로 정렬되었던 left 배열을 reverse 후 -1를 곱해준 배열에 right 배열을 concat 해준다
.reverse()
.map((item) => item * -1)
.concat(right);
}