이진탐색, Binary Search

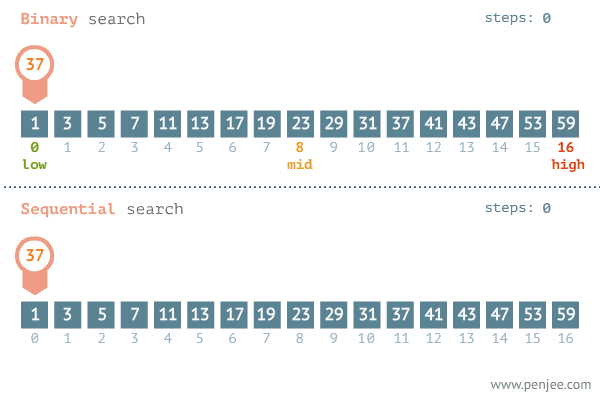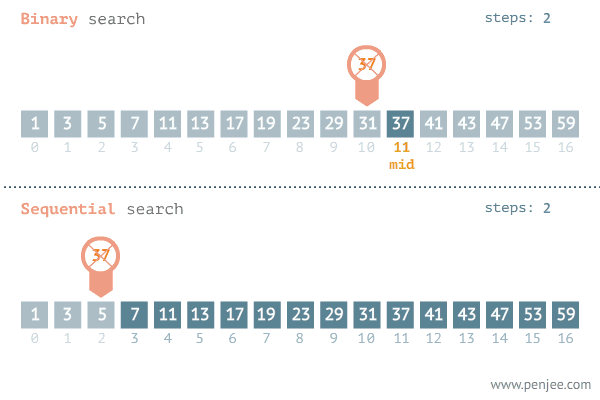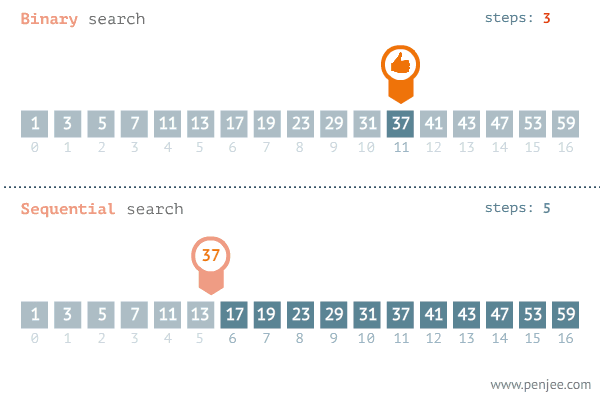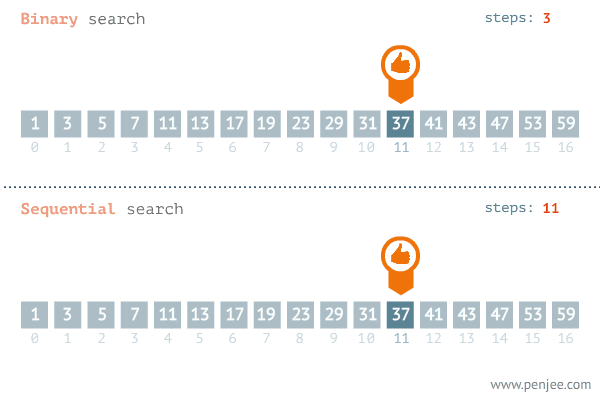
• 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
• 정렬된 배열을 사용함
• 변수 3개(start, end, mid)를 사용하여 탐색하며 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 탐색

방식

n개의 데이터를 가진 정렬된 배열 array

1. array[low] 에서부터 array[high]까지 탐색
   (이 때, low는 0번 인덱스의 값, high는 n-1번 인덱스의 값)

2. low와 high값을 이용해 중간값 mid 값을 구함
   mid = (low + high) / 2

3. array[mid] 값과 구하고자 하는 key값을 비교한다.
   3-1. key > mid : 구하고자 하는 값이 중간값보다 높다면 low를 mid +1로 만들어 줌 (왼쪽 반을 버림)
   3-2. key < mid : 구하고자하는 값이 중간값 보다 낮다면 high를 mid-1로 만들어 줌 (오른쪽 반을 버림)
   3-3. key == mid : 구하고자 하는 값을 찾음 중간값 리턴

4. low > high가 될 때까지 1~3번을 반복하면서 구하고자 하는 값을 찾는다.
   (이때까지 못 찾으면 탐색 실패 -1, false, error 등 return)

구현

1. 순환 호출을 이용한 이진 탐색 구현

int binarySearch1(int key, int low, int high) {
	int mid;

	if(low <= high) {
		mid = (low + high) / 2;

		if(key == arr[mid]) { // 탐색 성공 
			return mid;
		} else if(key < arr[mid]) {
			// 왼쪽 부분 arr[0]부터 arr[mid-1]에서의 탐색 
			return binarySearch1(key ,low, mid-1);  
		} else {
			// 오른쪽 부분 - arr[mid+1]부터 arr[high]에서의 탐색 
			return binarySearch1(key, mid+1, high); 
		}
	}

	return -1; // 탐색 실패 
}

2.반복을 이용한 이진 탐색 구현

int binarySearch2(int key, int low, int high) {
	int mid;

	while(low <= high) {
		mid = (low + high) / 2;

		if(key == arr[mid]) {
			return mid;
		} else if(key < arr[mid]) {
			high = mid - 1;
		} else {
			low = mid + 1;
		}
	}

	return -1; // 탐색 실패 
}

반복 구조를 사용하는 것이 재귀 호출로 구현하는 것보다 효율적

시간 복잡도

O(logN)
단계마다 탐색 범위를 반으로(÷2) 나누기때문
즉, 이진 탐색(이분 탐색)은 탐색 범위를 절반씩 줄이고, O(logN)의 시간 복잡도를 보장한다.

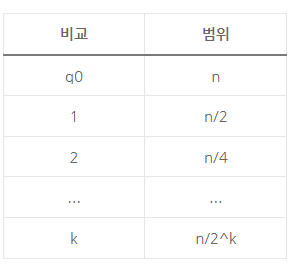
표의 마지막 행에서 n/2^k = 1 이므로, k = log 2 n 임을 알 수 있다.

따라서 이진 탐색의 시간 복잡도는 O(log n), 이 때 log는 log₂
로그의 밑이 변할 때, logan와 logbn는 오로지 상수 승수에 따라서만 달라지기에 빅-오 표기법에서는 버림함