5. MachLevelProg_1

Jongmin Choi·2024년 3월 20일
시스템프로그래밍
0

system-programming

목록 보기
1/2

3.2 Program Encodings

Turning C into object code

  • C파일 p1, p2를 p로 컴파일
    - Optimization: level O0~O3. 일반적으로 O2를 사용.
    - -o: output을 의미
gcc -O1 p1.c p2.c -o p
  1. preprocessing: 컴파일러가 #include로 명시된 파일을 삽입, #define으로 선언된 매크로 확장.

    C program (p1 p2) <- Text

  2. Compiler(gcc -S): 컴파일러가 p1.c와 p2.c 파일을 어셈블리어 코드를 생성.

    Asm program (p1.s p2.s) <- Text

  3. Assembler(gcc or as): 어셈블러가 p1.s와 p2.s 파일을 Binary Object 코드로 변환.

    Object program (p1.o p2.o) <- Binary

  4. Linker(gcc or ld): 링커가 p1.o와 p2.o를 static library(.a)들과 함께 합쳐저 최종 실행 파일인 p를 생성.

    Excutable program (p) <- Binary

Assembly programmer's view (x86-64 기준)

  • 기계수준 프로그램의 형식과 동작은 ISA(Instruction Set Architecture)에 의해 정의됨.
  • 기계수준 프로그램은 가상 주소(virtual address)를 사용하며, 이는 메모리가 매우 큰 바이트 배열처럼 보이는 메모리 모델을 제공.

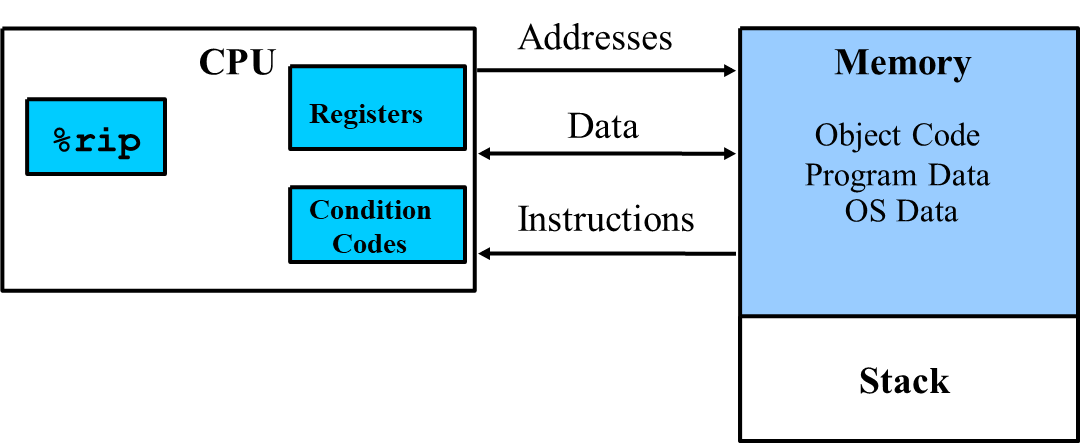
  • Program Counter(PC)
    - %rip(x86-64), %eip(x86)
    - 실행할 다음 instruction의 메모리 주소를 가리킴
  • Integer Register file
    - 64-bit에서 16개
    - 주소(포인터)와 정수를 저장, 프로그램 상태 추적
    - 함수의 리턴값, 임시값 저장
  • Condition Codes registers
    - 가장 최근에 수행한 산술/논리 instruction에 관한 상태 정보 저장
    - conditional branching에 사용(if, while...)
  • Vector registers
    - 하나 이상의 정수나 부동소수점 값들을 각각 저장
  • Memory
    - 가상 주소(virtual address): 메모리가 매우 큰 byte 배열로 보임
    - code, user data, (some) OS data 저장
    - Text: code
    - Data: BSS(Block Started Symbol), Data로 다시 나뉨
    - BSS가 클 수록 성능 저하
    - global variable 저장시 초기화가 되면 data, 안 했을 경우 BSS에 저장
    - Stack: procedure 지원
    - Heap: dynamic 메모리 할당

Compiling into assembly

code.c 파일의 수행 과정
// code.c
int sum(int x, int y) {
	int t = x + y;
	return t;
}
  1. compile(.c->.s)
# input
gcc -O -m64 -S code.c

# output
sum:
.LFB0:
     .cfi_startproc
     endbr64
     leal    (%rdi,%rsi), %eax
     ret
     .cfi_endproc
  • -m64 대신 -m32 옵션을 입력하면 32-bit 버전으로 컴파일 됨
  1. assemble(.s->.o)
# input
gcc -O1 -c code.c

# output viewed by gdb
0x0 <sum>:      0xf3    0x0f    0x1e    0xfa    0x8d    0x04    0x37    0xc3
0x8 <sum+8>:    0x04

# output viewed by objdump
0000000000000000 <sum>:
   0:   f3 0f 1e fa             endbr64
   4:   8d 04 37                lea    (%rdi,%rsi,1),%eax
   7:   c3                      retq
  • -c 옵션을 붙이지 않으면 main.c를 찾으려 해서 에러가 발생
  • gdb로 object 파일 보는 법
    - linux> % gdb code.o -> x/9xb sum (x: examine, 9xb: 16진수 9바이트)
  • objdump를 이용해 object 파일 보는 법(역어셈블러)
    - linux> objdump -d code.o
  • 역어셈블러(disassembler)는 GCC가 생성한 어셈블리 코드와는 다른 명명법을 인스트럭션에 사용. 접미어 'q'를 역어셈블러에서는 생략하지 않고 붙임(안전하게 생략 가능)
  1. execute
// main.c
#include <stdio.h>
int sum(int x, int y);
int main() {
	sum(1, 3);
}
#input
gcc -O1 -o prog code.o main.c

3.3 Data Formats

  • 인텔 프로세서들이 16비트 구조를 사용하다 추후에 32비트로 확장.
    - 16-bit: word
    - 32-bit: double word
    - 64-bit: quad word
C declarationIntel data typeAssembly-code suffixSize (bytes)
charByteb1
shortWordw2
intDouble wordl4
longQuad wordq8
char *Quad wordq8
floatSingle precisions4
doubleDouble precisionl8

Sizes of C data types in x86-64. (64비트 머신에서 포인터는 8바이트를 가짐)

3.4 Accessing Information

  • x86-64 CPU는 64비트 값을 저장할 수 있는 16개의 general-purpose 레지스터를 보유
  • 레지스터들은 32비트로 확장하면서 'e', 64비트로 확장하면서 'r'로 시작함
  • 16개의 레지스터 하위 바이트들에 저장된 다양한 크기와 데이터에 대해 연산 가능. LSB부터 각각 16비트는 2바이트, 32비트는 4바이트, 64비트는 레지스터 전체에 접근
  • 인트스럭션들이 레지스터를 목적지로 할 때, 1바이트(b)/2바이트(w)를 생성하는 경우 나머지 바이트들은 변경없이 유지. 4바이트(l)는 상위 4바이트를 0으로 설정

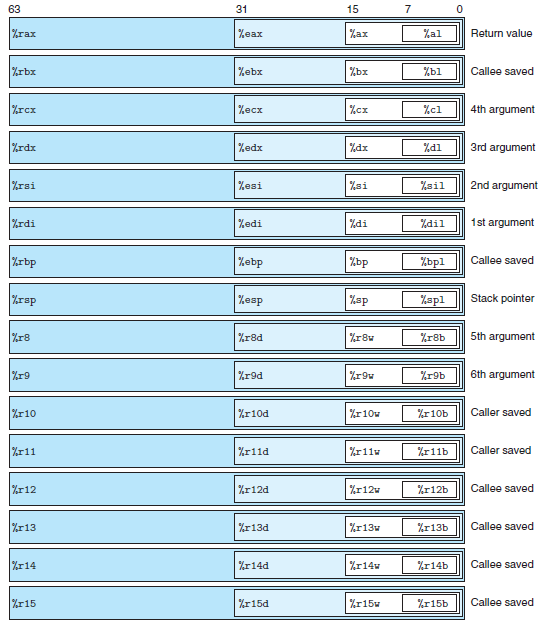
Integer registers

3.4.1 Operand Specifiers

  • 대부분의 instruction들은 1~2개의 operand를 가짐
    - Source: constant($), 메모리로부터 읽어온 값
    - Destination: 레지스터, 메모리
  • Type
    - Immediate :constant−Register: constant - Register %: 각각 16개의 64-bit(%rax...), 32-bit(%eax...), 16-bit(%ax...), 8-bit(%al...) - Memory (): effective address에 의해 메모리 접근 - $ Imm(r{b},r{i},s) = M[Imm + R[r_{b}] + R[r_{i}] \cdot s] $$ 중에서 effective address는 다음과 같다. $$ Imm + R[r_{b}] + R[r_{i} ]$$

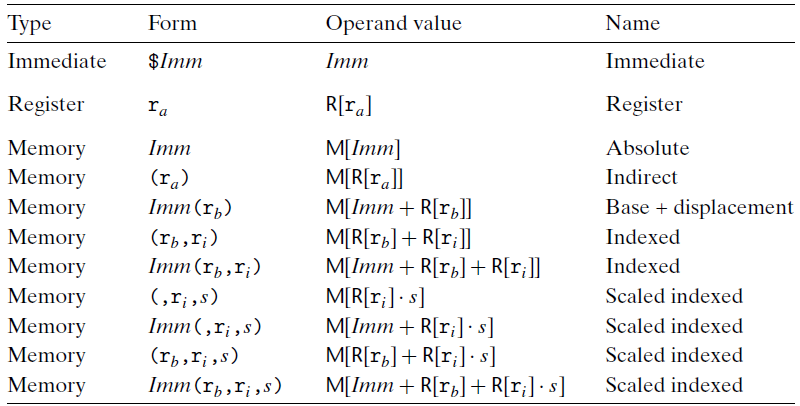
Operand forms. scaling factor s는 1, 2, 4, 8 중에 하나이다.

3.4.2 Data Movement Instructions

  1. Simple data movement instructions(MOV 클래스)

    • src에서 dest로 어떤 변환도 하지 않고 복사
    • Source operand: 상수, 레지스터, 메모리
    • Destination operand: 레지스터, 메모리 주소
    • 레지스터 바이트 크기에 따라 나뉨: movb(1), movw(2), movl(4), movq(8)
    • movl의 dest가 레지스터이면, 상위 4바이트를 0으로 설정
    • movabsq: 64-bit 상수를 다루기 위해 쓰임(Imm->Reg만 가능)
    • 1개의 인스트럭션에서 Mem->Mem로 이동 불가능! 2개의 인스트럭션으로 Mem->Reg 후 Reg->Mem 해야함

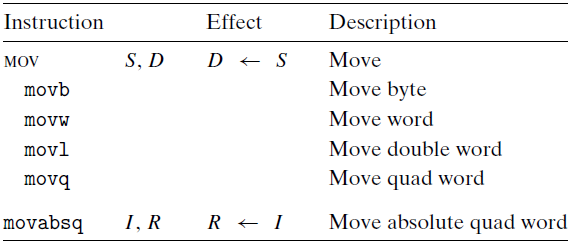
  2. Extending data movement instructions

    • 작은 src값을 더 큰 dest으로 옮길 때 사용함
    • Source operand: 레지스터, 메모리
    • Destination operand: 레지스터

    1. Zero-extending data movement instructions(MOVZ 클래스)

      • dest의 빈 자리를 모두 0으로 채움
      • movz _ _ 에서 마지막 두 자리는 데이터 크기로 첫 번째는 src, 두번째는 dest 크기를 나타냄
      • movzlq는 존재하지 않음. movl 인스트럭션을 대신 사용

    2. Sign-extending data movement instructions(MOVS 클래스)

      • dest의 빈 자리를 모두 src의 MSB로 채움(부호를 확장)
      • movs _ _ 에서 마지막 두 자리는 데이터 크기로 첫 번째는 src, 두번째는 dest 크기를 나타냄
      • zero-extended와 다르게 movslq 인스트럭션이 존재
      • cltq: 오퍼랜드가 없으며, 항상 src를 %eax로, dest를 %rax로 부호 확장 결과를 만듦. movslq %eax, %rax 와 동일한 효과지만 더 압축적인 인코딩을 가짐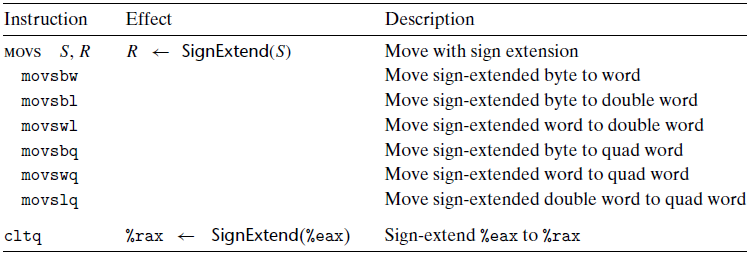

3.4.3 Data Movement Example

(a) C code

long exchange(long *xp, long y) {
	long x = *xp;
	*xp = y;
	return x;
}

(b) Assembly code

# long exchange(long *xp, long y)
# xp in %rdi, y in %rsi
exchange:
  movq (%rdi), %rax # Get x at xp. Set as return value.
  movq %rsi, (%rdi) # Store y at xp.
  ret # Return.
  • C에서 "포인터"는 어셈블리어에서는 "주소"이다.
  • 지역 변수들은 종종 레지스터에 저장된다.(메모리 접근보다 더 빠른 속도)

3.4.4 Pushing and Popping Stack Data

스택(stack): 후입선출(Last-In, First-Out) 형태로만 추가(push), 제거(pop) 가능

  • 모두 한 개의 operand만 가짐
  • push, pop 연산은 스택의 한쪽 끝(top)에서만 가능
  1. pushq: 스택에 데이터를 추가하는 연산
    • Source operand: 추가할 데이터
    • 스택 포인터를 8 감소 후 새로운 top에 src를 저장
# pushq %rbp. equivalent to the following pair of instructions:
subq $8,%rsp # Decrement stack pointer
movq %rbp,(%rsp) # Store %rbp on stack
  • 위 2개의 인스트럭션과 동일한 동일. 이는 8바이트가 필요하지만, pushq는 1바이트 machine code로 인코딩됨.
  1. popq: 스택의 데이터를 제거하는 연산
    • Destination operand: 추출을 위한 데이터 목적지
    • top에 있는 데이터를 추출 후 스택 포인터를 8 증가
    • 가장 최근에 추가된 값이 제거됨
    • pop 연산 이후에도 그 데이터는 여전히 스택에 남아있음
  • 스택의 top 원소가 가장 낮은 주소를 가지며, 스택 포인터 %rsp가 top의 주소를 저장
# popq %rax. equivalent to the following pair of instructions:
movq (%rsp),%rax # Read %rax from stack
addq $8,%rsp # Increment stack pointer
  • 표준 메모리 주소지정 방법(standard memory addressing method)을 이용하여 스택 내 임의의 위치에 접근 가능
    - Ex) movq 8(%rsp), %rdx로 스택의 두 번째(top의 바로 다음) 원소에 접근


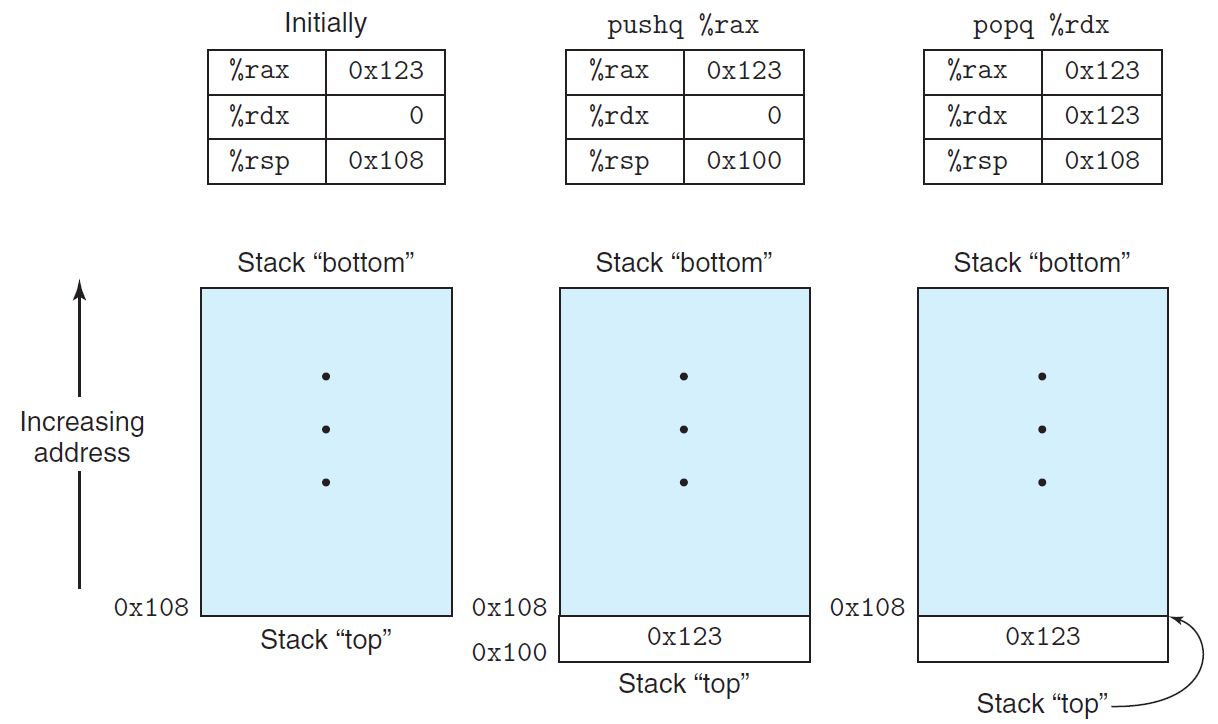
3.5 Arithmetic and Logical Operations

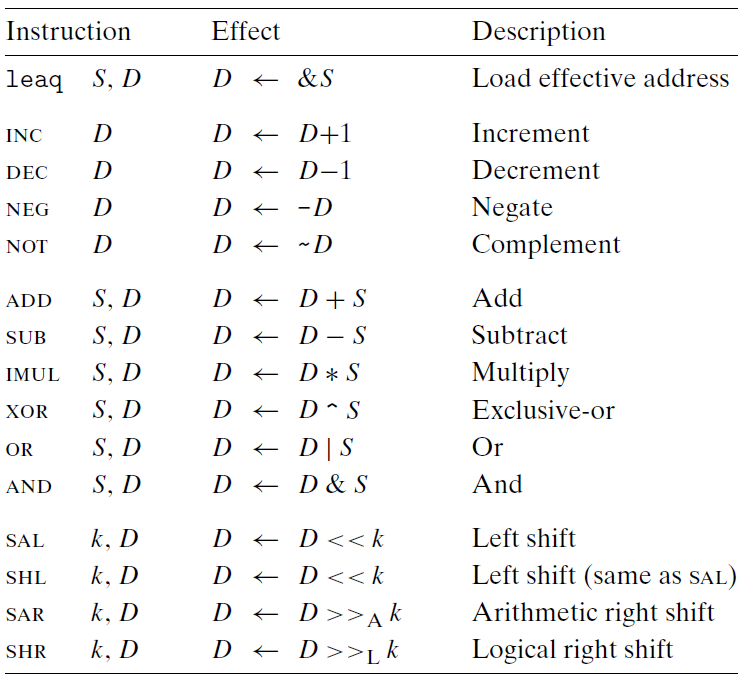
3.5.1 Load Effective Address

  • leaq: 유효 주소를 레지스터에 저장
    - Source operand: 유효 주소
    - Destination operand: 레지스터
    - 메모리를 전혀 참조하지 않음
    - 메모리 참조에 사용되는 포인터를 생성하기 위해 사용

Example

long scale(long x, long y, long z) {
	long t = x + 4 * y + 12 * z;
	return t;
}
# long scale(long x, long y, long z)
# x in %rdi, y in %rsi, z in %rdx
scale:
  leaq (%rdi,%rsi,4), %rax # x + 4*y
  leaq (%rdx,%rdx,2), %rdx # z + 2*z = 3*z
  leaq (%rax,%rdx,4), %rax # (x+4*y) + 4*(3*z) = x + 4*y + 12*z
  ret

3.5.2 Unary and Binary Operations

  1. 단항 연산
    • operand 하나가 src, dest로 동시에 사용: 레지스터, 메모리 위치
    • inc_(increment), dec_(decrement), neg_(negate), not_(complemet)
  2. 이항 연산
    • 첫 번째 operand가 src, 두 번째 operand가 src이자 dest
    • Source operand: 상수, 레지스터, 메모리
    • Source & Destination operand: 레지스터, 메모리
    • mov 인스트럭션과 마찬가지로 1개의 인스트럭션에서 Mem->Mem로 이동 불가능! 2개의 인스트럭션으로 Mem->Reg 후 Reg->Mem 해야함
    • add_(+), sub_(-), imul_(/), xor_(^), or_(|), and_(&)

3.5.3 Shift Operations

  • 첫 번재 operand가 shift할 크기(k), 두 번째 operand가 shift할 값
  • k(shift amount): 원칙적으로 255(2^8 - 1)까지 가능
    - immediate 값이나 %cl(단일 바이트 레지스터)로 명시할 수 있음
    - w비트 데이터에 적용되는 amount(m)는 %cl의 하위 log2 (w) 비트로 결정
    - Ex) %cl = 0xFF (1111 1111)
    - salb: 하위 3비트(log2 8 = 3) -> 0000 0111 -> 3
    - salw: 하위 4비트 (log2 16 = 4) -> 0000 1111 -> 15
    - sall: 하위 5비트 (log2 32 = 5) -> 0001 1111 -> 31
    - salq: 하위 6비트 (log2 64 = 6) -> 0011 1111 -> 63
  • Destination operand: 레지스터, 메모리
  • sal_, shr_: 왼쪽으로 shift후 우측부터 0을 채움(산술, 논리 상관없이 동일한 효과)
  • sar_: 오른쪽으로 shift후 죄측부터 0을 채움(산술 shift)
  • shr_: 오른쪽으로 shift후 MSB(부호 비트)를 채움(논리 shift)

3.5.5 Special Arithmetic Operations

  • oct word: x86-64 인스트럭션 set은 128-bit(16-byte) 숫자 관련 연산을 제한적으로 지원

  • 콜론(:)으로 두 레지스터가 연결되어 함께 하나의 더 큰 레지스터로 취급. 연산 결과의 상위 64-bit를 앞에, 하위 64-bit를 뒤에 있는 레지스터에 저장.

  • imulq: signed 정수 곱셈 연산으로, 두 가지 형식 가능
    1. 두 개의 operand를 사용하여 64-bit 결과를 생성(*u_64, *t_64)
    2. src operand 한 개만 사용
    - src와 %rax의 곱을 수행하여 128-bit의 결과를 %rdx:%rax에 저장.

  • mulq: unsigned 정수 곱셈 연산
    - src operand 한 개만 사용
    - src와 %rax의 곱을 수행하여 128-bit의 결과를 %rdx:%rax에 저장.

# void store_uprod(uint128_t *dest, uint64_t x, uint64_t y)
# dest in %rdi, x in %rsi, y in %rdx
store_uprod:
  movq %rsi, %rax # Copy x to multiplicand
  mulq %rdx # Multiply by y
  movq %rax, (%rdi) # Store lower 8 bytes at dest
  movq %rdx, 8(%rdi) # Store upper 8 bytes at dest+8
  ret

  • cqto: %rax 레지스터의 부호를 확장
    - operand가 없음
    - %rax의 부호 비트(MSB)를 확장하여 %rdx 전체에 복사
    - 주로 idivq 인스트럭션을 수행하기 전에 사용

  • idivq, divq: 정수 나눗셈 연산
    - 각각 signed/unsigned 128-bit 피제수(dividened)로, %rdx:%rax에 저장
    - src로 %rdx:%rax를 나누어 몫은 %rax, 나머지는 %rdx에 저장
    - 수행 전에 %rdx의 모든 비트들은 %rax의 부호 비트로 설정되어 있어야 함

# void remdiv(long x, long y, long *qp, long *rp)
# x in %rdi, y in %rsi, qp in %rdx, rp in %rcx
remdiv:
  movq %rdx, %r8 # Copy qp
  movq %rdi, %rax # Move x to lower 8 bytes of dividend
  cqto # Sign-extend to upper 8 bytes of dividend
  idivq %rsi # Divide by y
  movq %rax, (%r8) # Store quotient at qp
  movq %rdx, (%rcx) # Store remainder at rp
  ret
profile
Jongmin Choi
차곡차곡 정리하는 개발 공부일지
다음 포스트

6. MachLevelProg_2

0개의 댓글

관련 채용 정보