[C++] 백준 13174 - 괄호

JongPark·2022년 5월 19일
분할 정복을 이용한 거듭제곱수학정수론
7

Baekjoon

목록 보기
6/11
post-thumbnail

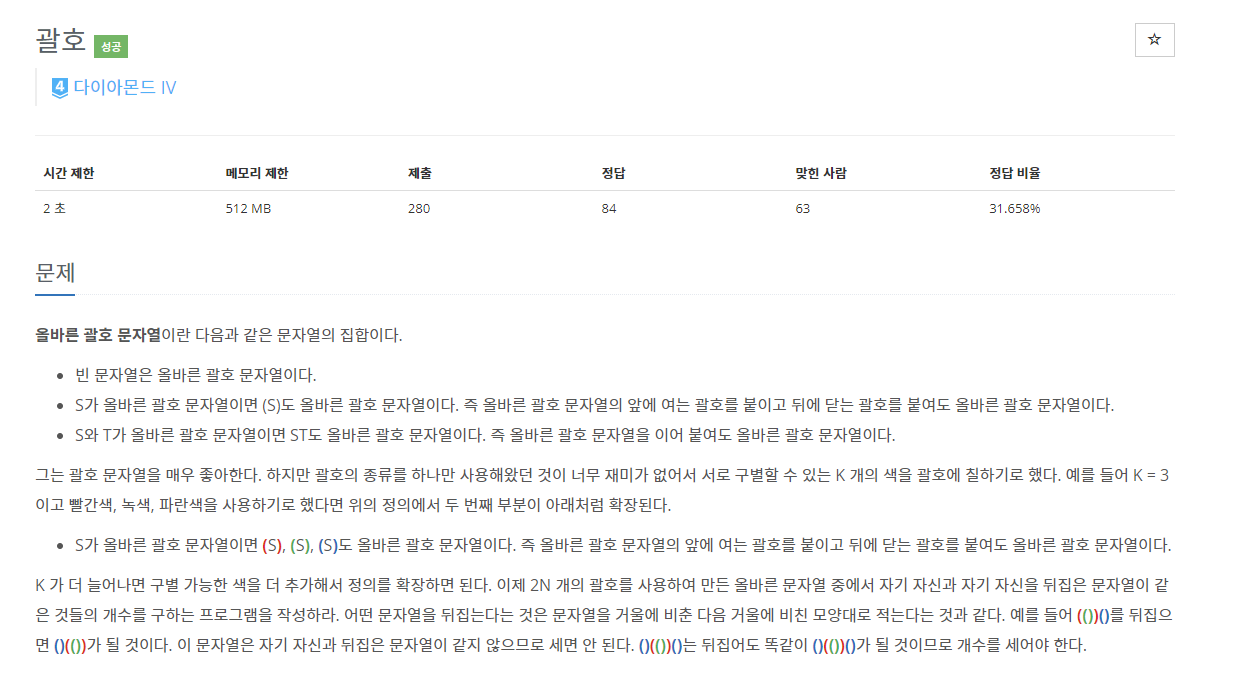
jbs30_jsh 님의 풀이를 보고 영감을 받아 작성한 글입니다.

우선 각각의 nn에 대해서, 대칭 축 기준 왼쪽에 kk쌍의 괄호가 존재하는 경우의 수를 h(n,k)h(n, k)라고 정의합시다. 그러면 아래와 같은 식이 성립하게 됩니다.

h(n,k)=h(n−1,k−1)+h(n−1,k)h(n, k) =h(n - 1,k - 1) + h(n - 1, k)
∴h(1,0)=1\therefore h(1, 0) = 1

문제를 보면 색깔 KK개가 주어집니다. 만약에 대칭 축 기준으로 왼쪽에 kk쌍의 괄호가 있다면 색칠하는 경우의 수는 Kn−kK^{n-k}가 됩니다.

이 때, Kn−kh(n,k)K^{n-k}h(n,k) 를 모두 더하면 우리가 원하는 답이 도출됩니다. 이것을 s(n)s(n)이라 정의하고, 또한 어떤 nn에 대해 대칭 축 기준으로 한 쪽에만 존재할 수 있는 최대 괄호 쌍 개수를 L(n)L(n)이라 정의합시다.

이 때,

s(n)=∑i=0L(n)Kn−ih(2n+1,i)s(n)=\sum\limits_{i=0}^{L(n)}K^{n-i}h(2n+1, i)

이며, 또한 L(2n)=L(2n+1)=nL(2n)=L(2n+1)=n 이라는 사실을 알 수 있습니다..

s(2n+1)/K=∑i=0nK2n−ih(2n+1,i)s(2n+1)/K=\sum\limits_{i=0}^nK^{2n-i}h(2n+1,i)
s(2n)=∑i=0nK2n−ih(2n,i)s(2n)=\sum\limits_{i=0}^nK^{2n-i}h(2n,i)
s(2n+1)/K−s(2n)s(2n+1)/K - s(2n)
=∑i=0nK2n−ih(2n,i−1)=\sum\limits_{i=0}^{n}K^{2n-i}h(2n,i - 1)
=∑i=0nK2n−i−1h(2n,i)=\sum\limits_{i=0}^nK^{2n-i-1}h(2n,i)
=s(2n)/K−Kn−1h(2n,n)=s(2n)/K-K^{n-1}h(2n,n)
∴s(2n+1)=s(2n)(K+1)−Knh(2n,n)\therefore s(2n+1)=s(2n)(K+1)-K^nh(2n,n)

이 때, h(2n,n)h(2n,n)에 대해서도 살펴봅시다.

s(2n)=∑i=0nK2n−ih(2n,i)s(2n)=\sum\limits_{i=0}^nK^{2n-i}h(2n,i)
ks(2n−1)=∑i=0n−1K2n−ih(2n−1,i)ks(2n-1)=\sum\limits_{i=0}^{n-1}K^{2n-i}h(2n-1,i)
s(2n)−ks(2n−1)=Knh(2n,n)+∑i=0n−1K2n−ih(2n−1,i−1)s(2n)-ks(2n-1)=K^nh(2n,n)+\sum\limits_{i=0}^{n-1}K^{2n-i}h(2n-1,i-1)

=Knh(2n,n)+∑i=0n−2K2n−i−1h(2n−1,i)=s(2n−1)+Knh(2n,n)−Knh(2n−1,n−1)=K^nh(2n,n)+\sum\limits_{i=0}^{n-2}K^{2n-i-1}h(2n-1, i)=s(2n-1)+K^nh(2n,n)-K^nh(2n-1,n-1)

이 때 h(2n,n)h(2n,n)의 의미는, 중심축을 기준으로 좌우 각각 nn개의 괄호들이 위치함을 알 수 있습니다. 한 쪽에 괄호를 배치하면 다른 쪽 괄호의 배치는 저절로 정해지기에, 괄호를 올바르게 배열하는 경우의 수는 CnC_n번째 카탈란 수 입니다.

카탈란 수란

C0=1andCn=∑i=0n−1CiCn−i−1forn≥1C_0=1\quad\mathsf{and} \quad Cn=\sum\limits_{i=0}^{n-1}C_iC_{n-i-1}\quad\mathsf{for}\quad n\geq1

라는 점화식 또는

Cn=(2n)!n!(n+1)!C_n=\frac{(2n)!}{n!(n+1)!}

라는 조합으로 나타내어 지는 수열입니다.

따라서, h(2n,n)=h(2n−1,n−1)=Cnh(2n,n)=h(2n-1,n-1)=C_n임을 알 수 있습니다.

s(2n)=s(2n−1)(K+1)s(2n)=s(2n-1)(K+1)
s(2n+1)=s(2n)(K+1)−KnCn=s(2n−1)(K+1)2−KnCns(2n+1)=s(2n)(K+1)-K^nC_n=s(2n-1)(K+1)^2-K^nC_n
s(2n+1)(K+1)2n=s(2n−1)(K+1)2n−2−(K(K+1)2)nCn\frac{s(2n+1)}{(K+1)^{2n}}=\frac{s(2n-1)}{(K+1)^{2n-2}}-\left(\frac{K}{(K+1)^2}\right)^nC_n
bn=s(2n+1)(K+1)2nb_n=\frac{s(2n+1)}{(K+1)^{2n}}
bn=bn−1−(K(K+1)2)nCnb_n=b_{n-1}-\left(\frac{K}{(K+1)^2}\right)^nC_n
bn−1−bn=(K(K+1)2)nCnb_{n-1}-b_n=\left(\frac{K}{(K+1)^2}\right)^nC_n
K−bn=∑i=1n(K(K+1)2)iCiK-b_n=\sum\limits_{i=1}^{n}\left(\frac{K}{(K+1)^2}\right)^iC_i
bn=K−∑i=1n(K(K+1)2)iCib_n=K-\sum\limits_{i=1}^{n}\left(\frac{K}{(K+1)^2}\right)^iC_i
∴s(2n+1)=K(K+1)2n−∑i=1nKi(K+1)2n−2iCi\therefore s(2n+1)=K(K+1)^{2n}-\sum\limits_{i=1}^nK^i(K+1)^{2n-2i}C_i

시간복잡도는 O(nlog⁡n)O(n\log n)에 동작합니다.

코드를 처음에는 python으로 구현하였으나, 이 쓰레기같은 언어가 시간을 버티지 못하여 C++로 재구현하였습니다.

#include <iostream>
#define MOD 1000000007
using namespace std;
long long power(long long x, long long y) {
	long long r = 1;
	while (y) {
		if (y & 1) r = (r * x) % MOD;
		y >>= 1;
		x = x * x % MOD;
	}
	return r;
}
int main() {
	long long result = 0, mate = 1, n, k, bracket, temp;
	cin >> n >> k;
	bracket = n / 2 - (n & 1 ? 0 : 1);
	result = k * power(k + 1, bracket * 2) % MOD;
	for (long long i = 1; i < bracket + 1; i++) {
		temp = power(k + 1, bracket * 2 - i * 2) * power(k, i) % MOD * mate % MOD;
		mate = mate * (i * 4 + 2) % MOD * power(i + 2, MOD - 2) % MOD;
		result -= temp;
		result %= MOD;
	}
	if (n % 2 == 0) {
		result *= k + 1;
		result %= MOD;
	}
	cout << (result + MOD) % MOD;
}

profile
JongPark
이전 포스트

[Python] 백준 18496 - Euclid's Algorithm

다음 포스트

[Python] 백준 10791 - Qanat

0개의 댓글