딥러닝 - 역전파(Backpropagation)

‍Juhee Kim·2021년 7월 4일

Deep Learning

목록 보기

4/7

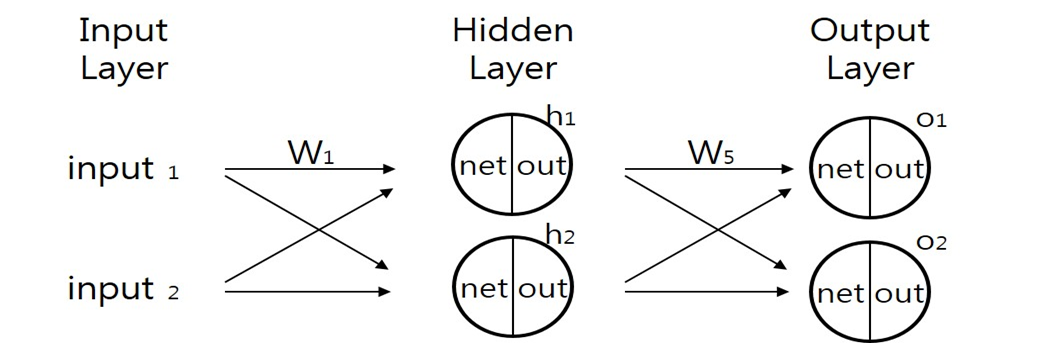
1. 학습할 신경망 구조를 선택한다.
입력층(Input layer) = 특징 수
은닉층(Hidden layer) : 은닉층 수, 각 은닉층 노드 수
출력층(Output layer) = 타겟 클래스 수

모델 제작 및 가중치 랜덤 초기화
모델에 값 넣고 output 값 계산
순방향 전파를 통해 비용함수 계산 (타겟값 – 출력값)
가중치 업데이트 :
역방향 전파를 통해 편미분값들 계산 + 경사하강법(or 다른 최적화 알고리즘) = 비용함수를 최소화한다.
어떤 중지 기준을 충족하거나 비용함수 최소화할 때 까지 3-5 단계 반복, 이 단계를 한 번 진행하는 것을 epoch 또는 iteration 이라 한다.

신경망의 성능을 측정하기 위해서 비용함수를 계산해야 한다.
한 데이터 샘플을 Forward Propagation를 시키고 마지막 출력층을 통과한 값과 이 데이터의 타겟값을 비교하여 loss 혹은 error를 계산한다.

여기서 한 데이터 포인트에서의 손실을 loss라 하고,
전체 데이터 셋의 loss를 합한 개념을 cost라고 한다.

최종목적은 이 오차에 관한 함수 E의 함수값을 0에 근사시키는 것이다.
오차가 0에 가까워진다면, 신경망은 학습에 사용된 input들과 그에 유사한 input에 대해서 우리가 원하는 output,
즉 정답이라고 할 수 있는 값들을 산출할 것이다.

신경망을 학습시키기 위한 알고리즘 중 하나로, 내가 원하는 타겟값과, 모델이 계산한 아웃풋값이 얼마나 차이가 있는지 계산한 후 그 오차값을 다시 뒤로 전파해 나가면서 각 노드가 가지고 있는 가중치 값을 업데이트 해 나가는 방법

목표는 가중치 w를 수정해 E가 최소가 되도록 만드는 것이다.

이를 위해 경사(Gradient)를 계산해서 경사가 작아지도록 가중치를 업데이트(gradient descent) 해야한다.

이를 위해 오차 E를 미분하는 과정이 필요한데, 모든 가중치가 오차 E에 영향을 미치고 있으므로 E를 각각의 가중치로 편미분한다.

경사하강법은 너무나 많은 신경망 안의 가중치 조합을 모두 계산하면 시간이 오래걸리기 때문에 효율적으로 이를 하기위해 고안된 방법입이다.

경사하강법을 사용하면 정확한 답을 얻지는 못할 수도 있다. 단계적으로 접근하는 것이기 때문에 만족스러운 정확도에 이를 때까지 계속해서 답을 찾아나가는 방식이다.

참조: https://sacko.tistory.com/19 [데이터 분석하는 문과생, 싸코]

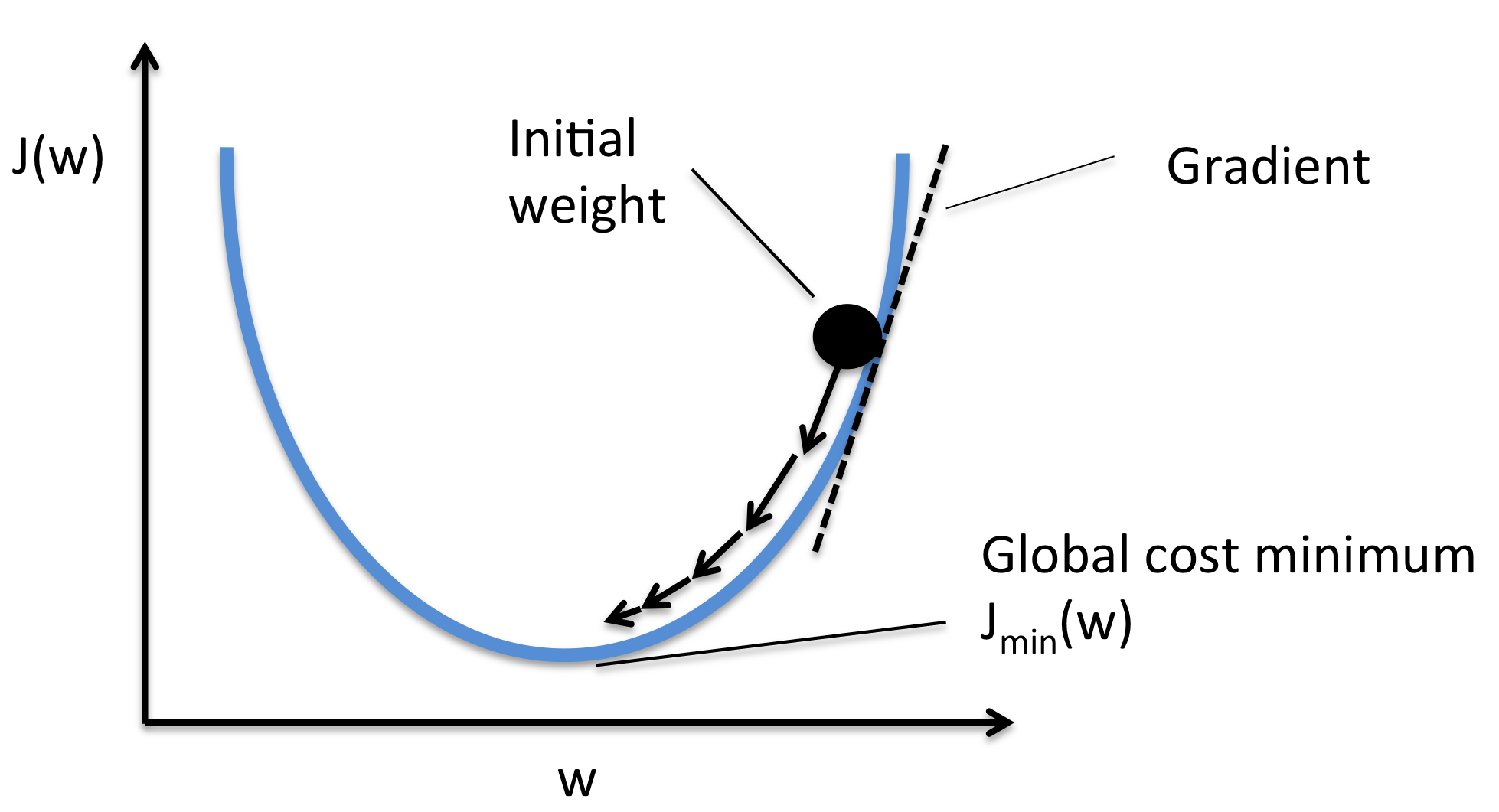
최적이란, 손실함수가 최솟값이 될 때의 매개변수 값이다.
기울기를 잘 이용해 함수의 최솟값을 찾으려는 것이 경사법이다.
여기에서 각 지점에서 함수의 값을 낮추는 방안을 제시하는 지표가 기울기이다.

경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다. 그런 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 그 기울어진 방향으로 나아가기를 반복한다. 이렇게 해서 함수의 값을 점차 줄이는 것이 경사법이다.

경사법은 최솟값을 찾으면 경사하강법, 최댓값을 찾으면 경사 상승법이라 한다.

경사하강법 알고리즘에는 여러가지 종류가 있다.

1) Stochastic Gradient Descent(SGD)
2) SGD의 변형된 알고리즘들(Momentum, RMSProp, Adam 등)
3) Newton's method 등 2차 최적화 알고리즘 기반 방법들(BFGS 등)

무작위로 뽑은 하나의 관측값 마다 기울기를 계산하고
바로 가중치를 업데이트 한다.

이를 극복하기 위해 배치방법과 SGD를 합친 Mini-batch 경사하강법, 모멘텀, AdaGrad, Adam을 사용할 수 있다.

찐문과생의 빅데이터 생존기🐣 열심히 할래용 (ง •_•)ง