하이퍼파라미터 값 찾기
신경망에는 하이퍼파라미터가 많이 등장한다.(ex. 각 층의 뉴런 수, 배치 크기, 학습률, 가중치 등...)
이 값들을 적절히 설정하지 않으면 모델의 성능이 크게 떨어진다. 앞으로 하이퍼파라미터를 다양한 값으로 설정하고 검정할 때, 시험 데이터(test set)을 사용해선 안 된다. 왜냐하면 시험 데이터에 과적합이 될 우려가 있기 때문이다.
이러한 이유로 하이퍼파라미터 전용 확인 데이터가 필요한데, 이를 검증 데이터(validation data)라고 부른다.
즉, 하이퍼파라미터의 적절성을 평가하는 데이터이다.
훈련 데이터 : 매개변수 학습
검증 데이터 : 하이퍼파라미터 성능 평가
시험 데이터 : 신경망의 범용 성능 평가
하이퍼 파라미터 튜닝 방식
- Babysitting AKA "Grad Student Descent". "육아", 혹은 대학원생 갈아넣기
이 방법은 소위 노가다...
- Grid Search
모든 경우의 수를 다 넣어보고 가장 성능이 좋게 만드는 모델의 하이퍼 파라미터를 찾는 것이다.(전수 탐색 방법)
시간이 매~우 오래 걸린다는 치명적인 단점을 가지고 있다.
- Random Search
지정된 범위내에서 무작위로 선정한 조건으로 모델을 돌려본 후 성능이 좋은 하이퍼파라미터를 찾는 방법이다.
Grid Search는 모든 파라미터가 동등하게 중요하다고 전제를 한다. 하지만 파라미터에 따라서 생각보다 더 크게 범위를 건너 뛰어야 되는 경우도 있다.
Random Search는 상대적으로 중요하다고 생각되는 파라미터에 대해 탐색을 더 하고, 덜 중요한 하이퍼파라미터에 대해서는 실험을 덜 할 수 있도록 해준다. 그러나 이것의 단점은 절대적으로 완벽한 하이퍼 파라미터를 찾아주진 않습니다. 하지만 Grid Search와 비교하면 덜 시간을 소모한다는 장점만으로도 충분히 빛을 발할 수 있다.
- Bayesian Methods
베이즈 정리를 중심으로 한 수학 이론을 구사항 더 엄밀하고 효율적으로 최적화를 수행한다.
베이지안 최적화 방식을 활용한다면 우리의 하이퍼 파라미터 튜닝 방식의 "하이퍼 파라미터 튜닝" 할 수 있다.
이전 탐색 결과를 반영해서 통계적인 모델을 만들고 그것을 바탕으로 다음 탐색을 해야 할 방향을 효과적으로 정해 이후의 하이퍼 파라미터 튜닝의 성능을 높이는 전략이다. 케라스의 keras-tuner를 쓰면 간단하게 활용할 수 있다.
튜닝가능한 파라미터 옵션
실험해볼 수 있는 하이퍼 파라미터의 종류는 다음과 같다 :
- batch_size
- training epochs
- optimization algorithms
- learning rate
- momentum
- activation functions
- dropout regularization
- hidden layer의 neuron 갯수
- etc.
Batch Size
배치 크기는 모델이 경사하강법을 통해 손실/오차 계산을 해서 모델의 가중치를 업데이트할 때 한번에 몇개의 관측치를 보게 되는지를 결정하는 파라미터이다.
우리가 찾고자 하는 가장 적절한 곳은 가중치를 업데이트 할 수 있을만큼의 충분한 정보를 제공할 수 있는 딱 충분한 양의 관측치들이다.
이 때 너무 큰 배치 크기를 고르게 되면 한번에 모든 데이터에 대한 Loss를 계산해야 하는 문제점이 있고, 학습 속도가 빠르기 때문에 주어진 epoch 안에 가중치를 충분히 업데이트 할 만큼의 iteration을 돌릴 수 없게 되기에 적당한 양을 고르는 것이 중요하다.
만약 너무 작은 사이즈를 고른다면 학습에 오랜 시간이 걸리고, 추정값에 노이즈가 많이 생기기 때문에 이 역시 지양해야 한다.
다양한 최적화 기법을 통해 최적의 하이퍼파라미터 조합을 찾을 수 있다.
출처: 하용호, 자습해도 모르겠던 딥러닝, 머리속에 인스톨 시켜드립니다
경사하강법의 단점
경사하강법은 무작정 기울어진 방향으로 이동하는 방식이기 때문에 탐색경로가 비효율적이어서 한참을 탐색하게 된다. 또한 SGD는 방향에 따라서 기울기 값이 달라지는 경우에 적합하지 않은데 최소값의 방향으로만 움직이기 때문에 본래의 최저점으로 기울기의 방향이 좀처럼 향하지 않게 되고 다른 방향을 가리키게 되어 비효율이게 되기도 한다.
이러한 단점을 개선해주는 모멘텀, AdaGrad, Adam 이라는 세 방법이 존재한다.
모멘텀 (Momentum)
모멘텀은 '운동량'을 뜻하는 단어이다. 오목한 밥그릇 한쪽에서 공을 굴리면 반대쪽에 있다가 바로 밑으로 내려가지않고 관성에 의해서 잠시 머물다 다시 내려오는 것을 상상해 보면 된다.

모멘텀은 옵티마이저가 최솟값을 overshooting(원래 가려고 했던 장소를 지나쳐 더 많이 가버렸다가 장기균형수준으로 수렴해 가는 현상) 하게 결정하는 속성이다.
모멘텀의 목적은 지역 최소점(local minima)에서 탈출하도록 시도하는 것이다.
- 모멘텀 구현 코드
class Momentum:
def __init__(self, lr = 0.01, momentum = 0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]인스턴스 변수 v가 물체의 속도다. v는 초기화 때는 아무 값도 담지 않고, 대신 update()가 처음 호출될 때 매개변수와 같은 구조의 데이터를 딕셔너리 변수로 저장한다.
모멘텀을 이용해서 최적화 문제를 풀어보면, 다음과 같은 그림이 그려진다.
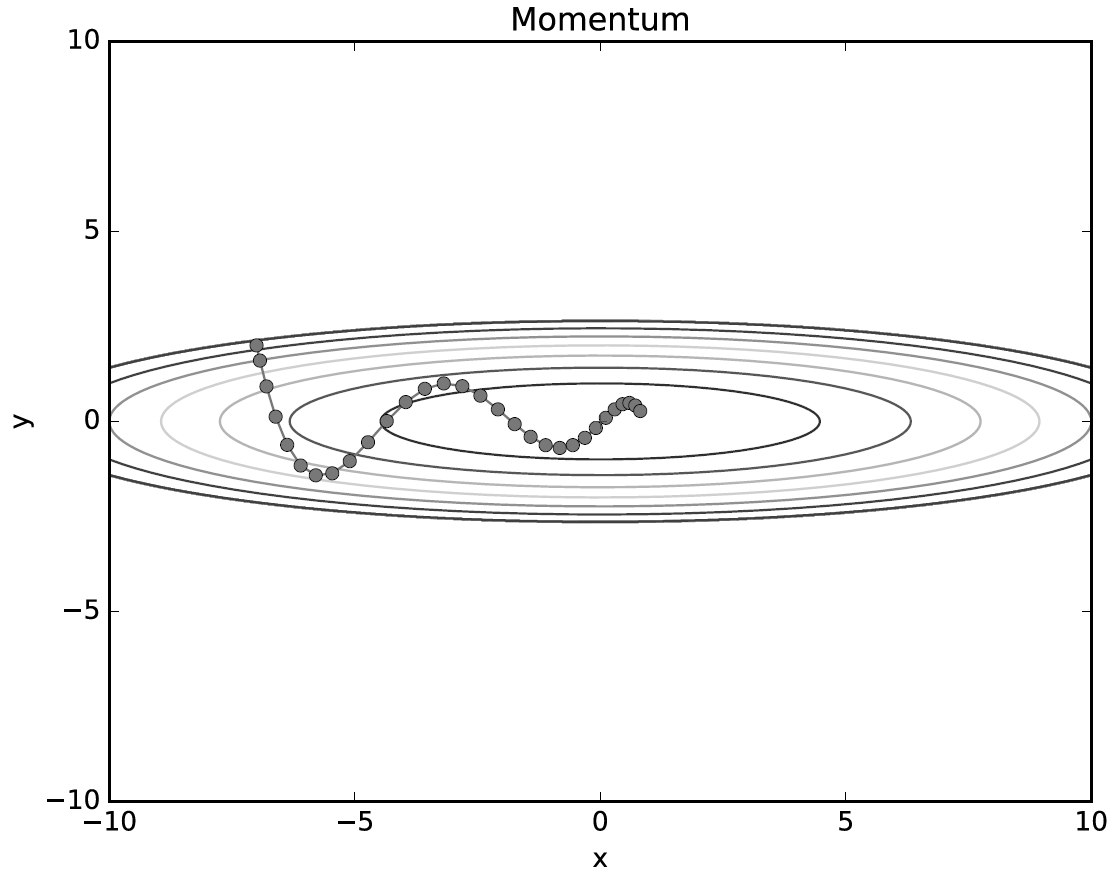
AdaGrad
신경망 학습에서는 학습률 값이 중요한데, 이 값이 너무 작으면 학습 시간이 너무 길어지고, 너무 크면 발산하여 학습이 제대로 이루어 지지 않는다.
이 학습률을 정하는 기술로 학습률 감소(learning rate decay)가 있다. 이는 학습을 진행하면서 학습률을 점차 줄여가는 방법이다. 즉, 처음에는 크게 학습하다가 조금씩 작게 학습한다는 뜻이다.
학습률을 서서히 낮추는 가장 간단한 방법은 매개변수 전체의 학습률 값을 일괄적으로 낮추는 것인데, 이를 더욱 발전시킨 것이 AdaGrad이다. 이는 '각각의' 매개변수에 '맞춤형' 값을 만들어 준다. (즉, 개별 매개변수에 적응적으로 학습률을 조정하며 학습을 진행한다.)
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
여기서 주의해야 할 점은 마지막 줄에서 1e-7이라는 작은 값을 더하는 부분이다.
이 작은 값은 self.h[key]에 0이 담겨있다 해도 0으로 나누는 일을 막아주는 역할을 해준다. 대부분의 딥러닝 프레임워크에서는 이 값도 인수로 설정할 수 있다.
- AdaGrad에 의한 최적화 갱신 경로
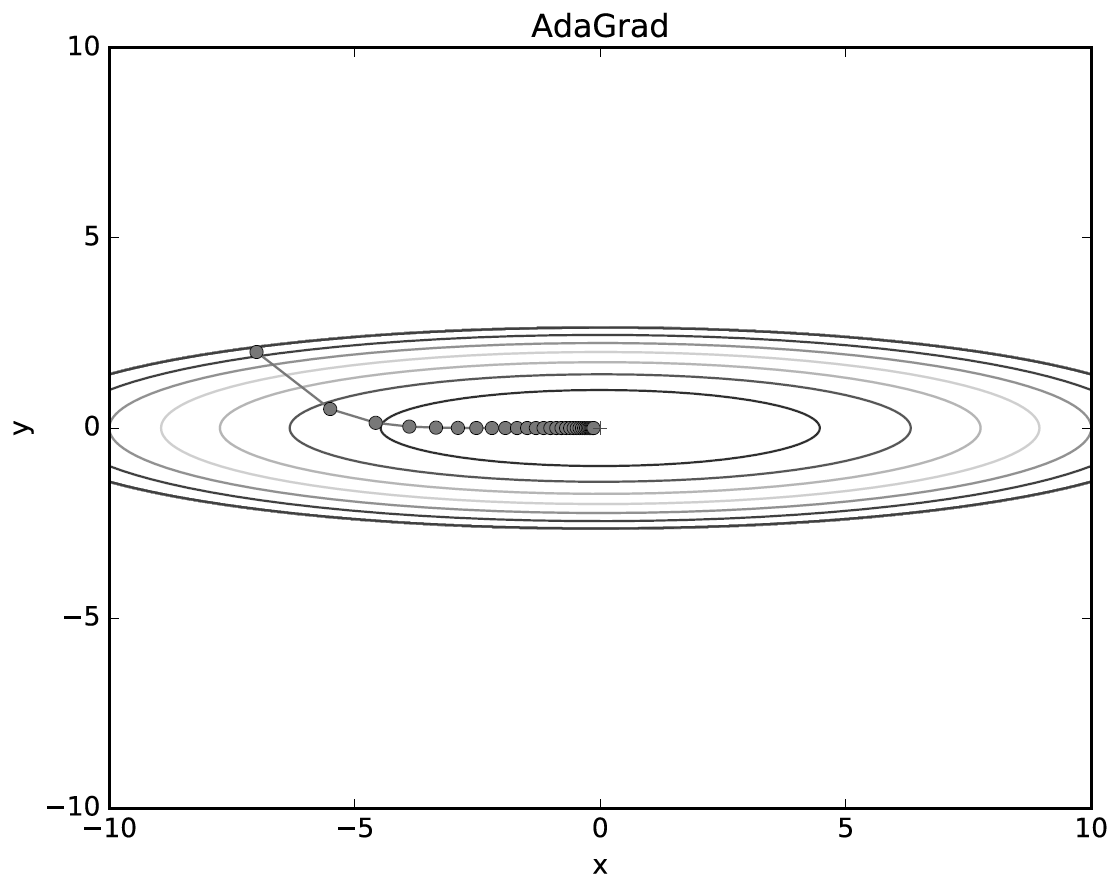
📢 AdaGrad는 과거의 기울기를 제곱하여 계속 더해간다. 그래서 학습을 진행할수록 갱신 강도가 약해지는데, 이를 무한히 계속 학습한다면 어느 순간 갱신량이 0이 되어 전혀 갱신되지 않게 된다.
이 문제를 개선한 기법으로 RMSProp이라는 방법이 있다. RMSProp은 과거의 모든 기울기를 균일하게 더해가는 것이 아니라, 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영한다.
이를 지수이동평균(Exponential Moving Average, EMA)라 하여, 과거 기울기의 반영 규모를 기하급수적으로 감소시킨다.
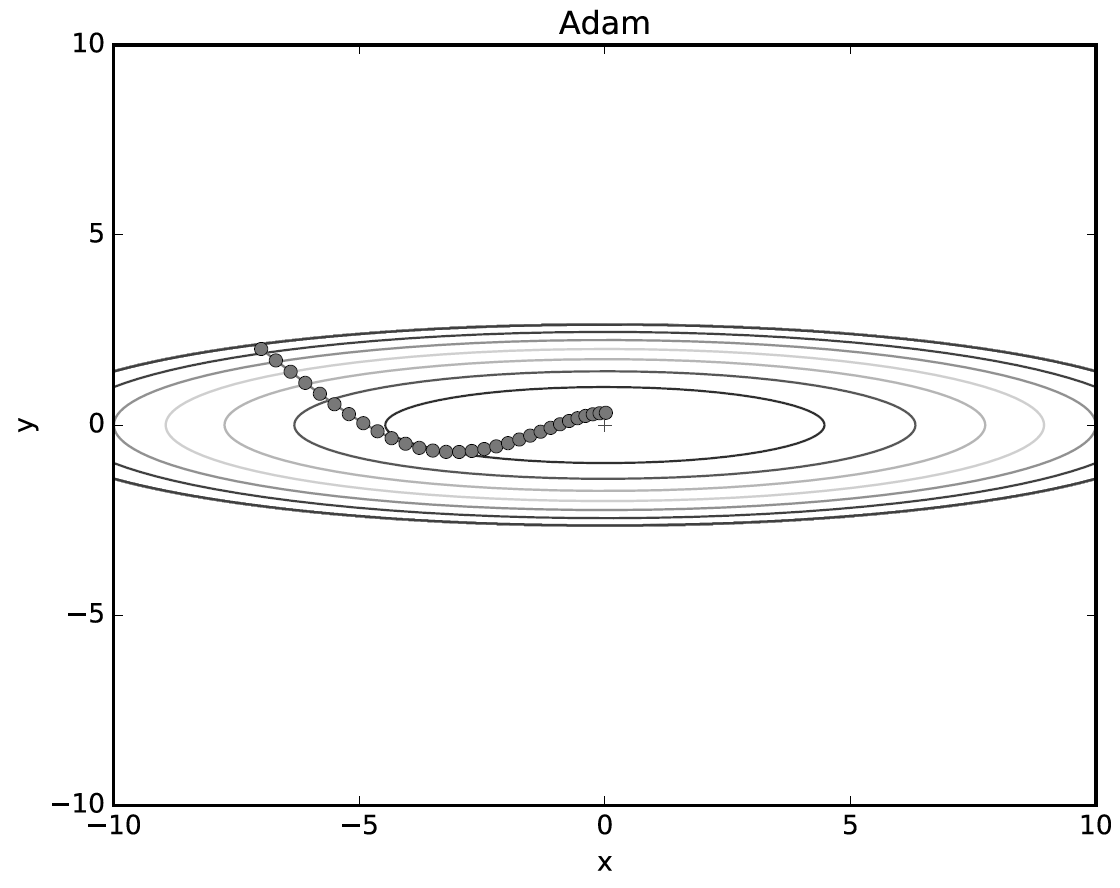
Adam
모멘텀은 공이 그릇 바닥을 구르는 듯한 움직임을 보였다. AdaGrad는 매개변수의 원소마다 적응적으로 갱신 정도를 조정했다. 이 두 기법을 융합한 기법이 바로 Adam이다.
두 방법의 이점을 조합하여, 매개변수 공간을 효율적으로 탐색해주고, 하이퍼파라미터의 '편향 보정'이 진행되는 특징을 가지고 있다. (더 자세한 것은 원 논문을 참고해야 함)
- Adam에 의한 최적화 갱신 경로